Class field theory
Encyclopedia
In mathematics
, class field theory is a major branch of algebraic number theory
that studies abelian extensions of number fields.
Most of the central results in this area were proved in the period between 1900 and 1950. The theory takes its name from the fact that the field extensions it studies, such as the Hilbert class field
, are associated to classes of ideals, so are called class fields. The ideal class group
(which is a basic object of study inside a single field of numbers K, such as a quadratic field
), is also seen as a Galois group
of a field extension
L/K: L is a field containing K and all the roots of a polynomial with coefficients in K.
These days the term is generally used synonymously with the study of all the abelian extension
s of algebraic number field
s, or more generally of local field
s and global field
s; an abelian extension being a Galois extension
with Galois group
that is an abelian group
(a finite abelian extension of Q is often simply called an abelian number field). In general terms, the objective is either to construct extensions of this type for a general number field K, or, to predict their arithmetical properties in terms of the arithmetical properties of K itself.
, so a compact topological group, and also abelian. The central aim of the theory is to describe G in terms of K.
The fundamental result of class field theory states that the group G is naturally isomorphic to the profinite completion of the idele class group CK of K with respect to the natural topology on CK (i.e. not the profinite completion of CK as an abstract group). Equivalently, for any finite Galois extension L of K, there is an isomorphism
of the maximal abelian quotient of the Galois group
of the extension with the quotient of the idele class group of K by the image of the norm
of the idele class group of L.
For example when K is the field of rational numbers the abelianized absolute Galois group G of K is (naturally isomorphic to) an infinite product of the group of units of the p-adic integers taken over all prime number
s p, and the corresponding maximal abelian extension of the rationals is the field generated by all roots of unity. This is known as the Kronecker–Weber theorem
, originally conjectured by Leopold Kronecker
.
In case K =
, the isomorphism of class field theory (i.e. the reciprocity map, or Artin reciprocity) also admits an explicit description due to the Kronecker–Weber theorem, which states that the maximal abelian extension of 
is given by adjoining all roots of unity to 
. Let us denote with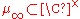
the group of all roots of unity, i.e. the torsion subgroup. The Artin reciprocity map is given by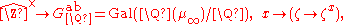
when it is arithmetically normalized, or given by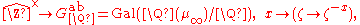
if it is geometrically normalized.
For a description of the general case see class formation
.
s decompose in the abelian extensions. The description is in terms of Frobenius elements, and generalises in a far-reaching way the quadratic reciprocity
law that gives full information on the decomposition of prime numbers in quadratic field
s. The class field theory project included the 'higher reciprocity laws' (cubic reciprocity
and so on), but is not limited to that one, classical, line of generalisation.
. The generalisation took place as a long-term historical project, involving quadratic form
s and their 'genus theory
', work of Ernst Kummer
and Leopold Kronecker
/Kurt Hensel
on ideals and completions, the theory of cyclotomic and Kummer extensions, conjectures of David Hilbert
, the reciprocity laws, and proofs by numerous mathematicians (Teiji Takagi
, Helmut Hasse
, Emil Artin
, Phillip Furtwängler and others). The crucial Takagi existence theorem
was known by 1920 and all the main results by about 1930. One of the last classical conjectures to be proved was the principalisation property. The first proofs of class field theory used substantial analytic methods. An important step was the introduction of ideles by Claude Chevalley
whose use essentially clarified and simplified structures which describe abelian extensions of global fields.
In the 1930s and subsequently the use of infinite extensions and the theory of Wolfgang Krull
of their Galois groups was found increasingly useful. It combines with Pontryagin duality
to give a clearer if more abstract formulation of the central result, the Artin reciprocity law. It is also basic to Iwasawa theory
.
After the results were reformulated in terms of group cohomology
which became a standard way to learn class field theory for several generations of number theorists.
One drawback of the cohomological method is its relative inexplicitness. As the result of contributions of John Tate
, Michiel Hazewinkel, Jurgen Neukirch
and also due to the work on explicit reciprocity formulas by many mathematicians, a very explicit and cohomology free presentation of class field theory was established in the nineties, see e.g. the book of Neukirch.
One of attempts to develop a more general class field theory which describes non-abealian extensions of global fields is the Langlands program
. Its development in the sixties and seventies provided a fresh impetus, and it is often viewed as 'non-abelian class field theory
', though that description does not include any kind of existence theorem and does not provide as much arithmetical information as the abelian class field theory.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, class field theory is a major branch of algebraic number theory
Algebraic number theory
Algebraic number theory is a major branch of number theory which studies algebraic structures related to algebraic integers. This is generally accomplished by considering a ring of algebraic integers O in an algebraic number field K/Q, and studying their algebraic properties such as factorization,...
that studies abelian extensions of number fields.
Most of the central results in this area were proved in the period between 1900 and 1950. The theory takes its name from the fact that the field extensions it studies, such as the Hilbert class field
Hilbert class field
In algebraic number theory, the Hilbert class field E of a number field K is the maximal abelian unramified extension of K. Its degree over K equals the class number of K and the Galois group of E over K is canonically isomorphic to the ideal class group of K using Frobenius elements for prime...
, are associated to classes of ideals, so are called class fields. The ideal class group
Ideal class group
In mathematics, the extent to which unique factorization fails in the ring of integers of an algebraic number field can be described by a certain group known as an ideal class group...
(which is a basic object of study inside a single field of numbers K, such as a quadratic field
Quadratic field
In algebraic number theory, a quadratic field is an algebraic number field K of degree two over Q. It is easy to show that the map d ↦ Q is a bijection from the set of all square-free integers d ≠ 0, 1 to the set of all quadratic fields...
), is also seen as a Galois group
Galois group
In mathematics, more specifically in the area of modern algebra known as Galois theory, the Galois group of a certain type of field extension is a specific group associated with the field extension...
of a field extension
Field extension
In abstract algebra, field extensions are the main object of study in field theory. The general idea is to start with a base field and construct in some manner a larger field which contains the base field and satisfies additional properties...
L/K: L is a field containing K and all the roots of a polynomial with coefficients in K.
These days the term is generally used synonymously with the study of all the abelian extension
Abelian extension
In abstract algebra, an abelian extension is a Galois extension whose Galois group is abelian. When the Galois group is a cyclic group, we have a cyclic extension. More generally, a Galois extension is called solvable if its Galois group is solvable....
s of algebraic number field
Algebraic number field
In mathematics, an algebraic number field F is a finite field extension of the field of rational numbers Q...
s, or more generally of local field
Local field
In mathematics, a local field is a special type of field that is a locally compact topological field with respect to a non-discrete topology.Given such a field, an absolute value can be defined on it. There are two basic types of local field: those in which the absolute value is archimedean and...
s and global field
Global field
In mathematics, the term global field refers to either of the following:*an algebraic number field, i.e., a finite extension of Q, or*a global function field, i.e., the function field of an algebraic curve over a finite field, equivalently, a finite extension of Fq, the field of rational functions...
s; an abelian extension being a Galois extension
Galois extension
In mathematics, a Galois extension is an algebraic field extension E/F satisfying certain conditions ; one also says that the extension is Galois. The significance of being a Galois extension is that the extension has a Galois group and obeys the fundamental theorem of Galois theory.The definition...
with Galois group
Galois group
In mathematics, more specifically in the area of modern algebra known as Galois theory, the Galois group of a certain type of field extension is a specific group associated with the field extension...
that is an abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
(a finite abelian extension of Q is often simply called an abelian number field). In general terms, the objective is either to construct extensions of this type for a general number field K, or, to predict their arithmetical properties in terms of the arithmetical properties of K itself.
Formulation in contemporary language
In modern language there is a maximal abelian extension A of K, which will be of infinite degree over K; and associated to A a Galois group G which will be a pro-finite groupPro-finite group
In mathematics, profinite groups are topological groups that are in a certain sense assembled from finite groups; they share many properties with their finite quotients.- Definition :...
, so a compact topological group, and also abelian. The central aim of the theory is to describe G in terms of K.
The fundamental result of class field theory states that the group G is naturally isomorphic to the profinite completion of the idele class group CK of K with respect to the natural topology on CK (i.e. not the profinite completion of CK as an abstract group). Equivalently, for any finite Galois extension L of K, there is an isomorphism
- Gal(L / K)ab → CK / NL/K CL
of the maximal abelian quotient of the Galois group
Galois group
In mathematics, more specifically in the area of modern algebra known as Galois theory, the Galois group of a certain type of field extension is a specific group associated with the field extension...
of the extension with the quotient of the idele class group of K by the image of the norm
Field norm
In mathematics, the norm is a mapping defined in field theory, to map elements of a larger field into a smaller one.-Formal definitions:1. Let K be a field and L a finite extension of K...
of the idele class group of L.
For example when K is the field of rational numbers the abelianized absolute Galois group G of K is (naturally isomorphic to) an infinite product of the group of units of the p-adic integers taken over all prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
s p, and the corresponding maximal abelian extension of the rationals is the field generated by all roots of unity. This is known as the Kronecker–Weber theorem
Kronecker–Weber theorem
In algebraic number theory, the Kronecker–Weber theorem states that every finite abelian extension of the field of rational numbers Q, or in other words, every algebraic number field whose Galois group over Q is abelian, is a subfield of a cyclotomic field, i.e. a field obtained by adjoining a root...
, originally conjectured by Leopold Kronecker
Leopold Kronecker
Leopold Kronecker was a German mathematician who worked on number theory and algebra.He criticized Cantor's work on set theory, and was quoted by as having said, "God made integers; all else is the work of man"...
.
In case K =
, the isomorphism of class field theory (i.e. the reciprocity map, or Artin reciprocity) also admits an explicit description due to the Kronecker–Weber theorem, which states that the maximal abelian extension of is given by adjoining all roots of unity to . Let us denote with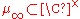the group of all roots of unity, i.e. the torsion subgroup. The Artin reciprocity map is given by
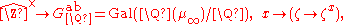
when it is arithmetically normalized, or given by
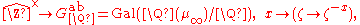
if it is geometrically normalized.
For a description of the general case see class formation
Class formation
In mathematics, a class formation is a structure used to organize the various Galois groups and modules that appear in class field theory. They were invented by Emil Artin and John Tate.-Definitions:...
.
Prime ideals
More than just the abstract description of G, it is essential for the purposes of number theory to understand how prime idealPrime ideal
In algebra , a prime ideal is a subset of a ring which shares many important properties of a prime number in the ring of integers...
s decompose in the abelian extensions. The description is in terms of Frobenius elements, and generalises in a far-reaching way the quadratic reciprocity
Quadratic reciprocity
In number theory, the law of quadratic reciprocity is a theorem about modular arithmetic which gives conditions for the solvability of quadratic equations modulo prime numbers...
law that gives full information on the decomposition of prime numbers in quadratic field
Quadratic field
In algebraic number theory, a quadratic field is an algebraic number field K of degree two over Q. It is easy to show that the map d ↦ Q is a bijection from the set of all square-free integers d ≠ 0, 1 to the set of all quadratic fields...
s. The class field theory project included the 'higher reciprocity laws' (cubic reciprocity
Cubic reciprocity
Cubic reciprocity is a collection of theorems in elementary and algebraic number theory that state conditions under which the congruence x3 ≡ p is solvable; the word "reciprocity" comes from the form of the main theorem, which states that if p and q are primary numbers in the...
and so on), but is not limited to that one, classical, line of generalisation.
History
The origins of class field theory lie in the quadratic reciprocity law proved by GaussGauss
Gauss may refer to:*Carl Friedrich Gauss, German mathematician and physicist*Gauss , a unit of magnetic flux density or magnetic induction*GAUSS , a software package*Gauss , a crater on the moon...
. The generalisation took place as a long-term historical project, involving quadratic form
Quadratic form
In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....
s and their 'genus theory
Genus theory
In the mathematical theory of games, genus theory in impartial games is a theory by which some games played under the misère play convention can be analysed, to predict the outcome class of games....
', work of Ernst Kummer
Ernst Kummer
Ernst Eduard Kummer was a German mathematician. Skilled in applied mathematics, Kummer trained German army officers in ballistics; afterwards, he taught for 10 years in a gymnasium, the German equivalent of high school, where he inspired the mathematical career of Leopold Kronecker.-Life:Kummer...
and Leopold Kronecker
Leopold Kronecker
Leopold Kronecker was a German mathematician who worked on number theory and algebra.He criticized Cantor's work on set theory, and was quoted by as having said, "God made integers; all else is the work of man"...
/Kurt Hensel
Kurt Hensel
Kurt Wilhelm Sebastian Hensel was a German mathematician born in Königsberg, Prussia.He was the son of the landowner and entrepreneur Sebastian Hensel, brother of the philosopher Paul Hensel, grandson of the composer Fanny Mendelssohn and the painter Wilhelm Hensel, and a descendant of the...
on ideals and completions, the theory of cyclotomic and Kummer extensions, conjectures of David Hilbert
David Hilbert
David Hilbert was a German mathematician. He is recognized as one of the most influential and universal mathematicians of the 19th and early 20th centuries. Hilbert discovered and developed a broad range of fundamental ideas in many areas, including invariant theory and the axiomatization of...
, the reciprocity laws, and proofs by numerous mathematicians (Teiji Takagi
Teiji Takagi
Teiji Takagi was a Japanese mathematician, best known for proving the Takagi existence theorem in class field theory....
, Helmut Hasse
Helmut Hasse
Helmut Hasse was a German mathematician working in algebraic number theory, known for fundamental contributions to class field theory, the application of p-adic numbers to local classfield theory and diophantine geometry , and to local zeta functions.-Life:He was born in Kassel, and died in...
, Emil Artin
Emil Artin
Emil Artin was an Austrian-American mathematician of Armenian descent.-Parents:Emil Artin was born in Vienna to parents Emma Maria, née Laura , a soubrette on the operetta stages of Austria and Germany, and Emil Hadochadus Maria Artin, Austrian-born of Armenian descent...
, Phillip Furtwängler and others). The crucial Takagi existence theorem
Takagi existence theorem
In class field theory, the Takagi existence theorem states that for any number field K there is a one-to-one inclusion reversing correspondence between the finite abelian extensions of K and the generalized ideal class groups defined via a modulus of K.It is called an existence theorem because a...
was known by 1920 and all the main results by about 1930. One of the last classical conjectures to be proved was the principalisation property. The first proofs of class field theory used substantial analytic methods. An important step was the introduction of ideles by Claude Chevalley
Claude Chevalley
Claude Chevalley was a French mathematician who made important contributions to number theory, algebraic geometry, class field theory, finite group theory, and the theory of algebraic groups...
whose use essentially clarified and simplified structures which describe abelian extensions of global fields.
In the 1930s and subsequently the use of infinite extensions and the theory of Wolfgang Krull
Wolfgang Krull
Wolfgang Krull was a German mathematician working in the field of commutative algebra.He was born in Baden-Baden, Imperial Germany and died in Bonn, West Germany.- See also :* Krull dimension* Krull topology...
of their Galois groups was found increasingly useful. It combines with Pontryagin duality
Pontryagin duality
In mathematics, specifically in harmonic analysis and the theory of topological groups, Pontryagin duality explains the general properties of the Fourier transform on locally compact groups, such as R, the circle or finite cyclic groups.-Introduction:...
to give a clearer if more abstract formulation of the central result, the Artin reciprocity law. It is also basic to Iwasawa theory
Iwasawa theory
In number theory, Iwasawa theory is the study of objects of arithmetic interest over infinite towers of number fields. It began as a Galois module theory of ideal class groups, initiated by Kenkichi Iwasawa, in the 1950s, as part of the theory of cyclotomic fields. In the early 1970s, Barry Mazur...
.
After the results were reformulated in terms of group cohomology
Group cohomology
In abstract algebra, homological algebra, algebraic topology and algebraic number theory, as well as in applications to group theory proper, group cohomology is a way to study groups using a sequence of functors H n. The study of fixed points of groups acting on modules and quotient modules...
which became a standard way to learn class field theory for several generations of number theorists.
One drawback of the cohomological method is its relative inexplicitness. As the result of contributions of John Tate
John Tate
John Torrence Tate Jr. is an American mathematician, distinguished for many fundamental contributions in algebraic number theory, arithmetic geometry and related areas in algebraic geometry.-Biography:...
, Michiel Hazewinkel, Jurgen Neukirch
Jürgen Neukirch
Jürgen Neukirch was a German mathematician known for his work on algebraic number theory....
and also due to the work on explicit reciprocity formulas by many mathematicians, a very explicit and cohomology free presentation of class field theory was established in the nineties, see e.g. the book of Neukirch.
One of attempts to develop a more general class field theory which describes non-abealian extensions of global fields is the Langlands program
Langlands program
The Langlands program is a web of far-reaching and influential conjectures that relate Galois groups in algebraic number theory to automorphic forms and representation theory of algebraic groups over local fields and adeles. It was proposed by ....
. Its development in the sixties and seventies provided a fresh impetus, and it is often viewed as 'non-abelian class field theory
Non-abelian class field theory
In mathematics, non-abelian class field theory is a catchphrase, meaning the extension of the results of class field theory, the relatively complete and classical set of results on abelian extensions of any number field K, to the general Galois extension L/K...
', though that description does not include any kind of existence theorem and does not provide as much arithmetical information as the abelian class field theory.