Kleinian group
Encyclopedia
In mathematics
, a Kleinian group is a discrete subgroup of PSL(2, C). The group PSL(2, C) of 2 by 2 complex matrices of determinant 1 modulo its center has several natural representations: as conformal transformations of the Riemann sphere
, and as orientation-preserving isometries of 3-dimensional hyperbolic space
H3, and as orientation preserving conformal
maps of the open unit ball B3 in R3 to itself. Therefore a Kleinian group can be regarded as a discrete subgroup acting on one of these spaces.
There are some variations of the definition of a Kleinian group: sometimes
Kleinian groups are allowed to be subgroups of PSL(2, C).2 (PSL(2, C) extended by complex conjugations), in other words to have orientation reversing elements, and sometimes they are assumed to be finitely generated, and sometimes they are required to act properly discontinuously on a non-empty open subset of the Riemann sphere. A Kleinian group is said to be of type 1 if the limit set is the whole Riemann sphere, and of type 2 otherwise.
The theory of general Kleinian groups was founded by and , who named them after Felix Klein
. The special case of Schottky group
s had been studied a few year before by Schottky.
, which acts by Möbius transformations on the Riemann sphere
. Classically, a Kleinian group was required to act properly discontinuously on a non-empty open subset of the Riemann sphere, but modern usage allows any discrete subgroup.
When Γ is isomorphic to the fundamental group
of a hyperbolic 3-manifold
, then the quotient space
H3/Γ becomes a Kleinian model of the manifold. Many authors use the terms Kleinian model and Kleinian group interchangeably, letting the one stand for the other.
Discreteness implies points in B3 have finite stabilizers, and discrete orbits under the group G. But the orbit Gp of a point p will typically accumulate on the boundary of the closed ball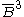
.
The boundary of the closed ball is called the sphere at infinity, and is denoted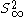 
. The set of accumulation points of Gp in 
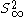is called the limit set of G, and usually denoted 
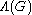. The complement 
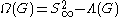is called the domain of discontinuity or the ordinary set or the regular set. Ahlfors' finiteness theorem implies that if the group is finitely generated then 
is a Riemann surface orbifold of finite type.
The unit ball B3 with its conformal structure is the Poincaré model
of hyperbolic 3-space. When we think of it metrically, with metric
it is a model of 3-dimensional hyperbolic space H3. The set of conformal self-maps of B3 becomes the set of isometries (i.e. distance-preserving maps) of H3 under this identification. Such maps restrict to conformal self-maps of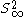
, which are Möbius transformations. There are isomorphisms
The subgroup
s of these groups consisting of orientation-preserving transformations are all isomorphic to the projective matrix group: PSL(2,C) via the usual identification of the unit sphere
with the complex projective line P1(C).
is a Kleinian group of the form PSL(2, Od), where d is a positive square-free integer
.
Examples of degenerate Kleinian groups include finite Kleinian groups (with empty limit set) and infinite cyclic Kleinian groups.
A Kleinian group is called reducible if all elements have a common fixed point on the Riemann sphere. Reducible Kleinian groups are elementary, but some elementary finite Kleinian groups are not reducible.
(a discrete subgroup of SL(2, R)) is a Kleinian group, and conversely any Kleinian group preserving the real line (in its action on the Riemann sphere) is a Fuchsian group. More generally, any Kleinian group preserving a circle or straight line in the Riemann sphere is conjugate to a Fuchsian group.
. When the Jordan curve is a circle or a straight line these are just conjugate to Fuchsian groups under conformal transformations. Finitely generated quasi-Fuchsian groups are conjugate to Fuchsian groups under quasi-conformal transformations. The limit set is contained in the invariant Jordan curve, and it is equal to the Jordan curve the group is said to be of type one, and otherwise it is said to be of type 2.
, and the quotient H3/G is a mirror orbifold with underlying space a ball. It is double covered by a handlebody
; the corresponding index
2 subgroup is a Kleinian group called a Schottky group
.
tessellation
of hyperbolic 3-space. The group of symmetries of the tessellation is a Kleinian group.
The existence of degenerate Kleinian groups was first shown indirectly by , and the first explicit example was found by Jørgensen. gave examples of doubly degenerate groups and space-filling curves associated to pseudo-Anosov map
s.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a Kleinian group is a discrete subgroup of PSL(2, C). The group PSL(2, C) of 2 by 2 complex matrices of determinant 1 modulo its center has several natural representations: as conformal transformations of the Riemann sphere
Riemann sphere
In mathematics, the Riemann sphere , named after the 19th century mathematician Bernhard Riemann, is the sphere obtained from the complex plane by adding a point at infinity...
, and as orientation-preserving isometries of 3-dimensional hyperbolic space
Hyperbolic space
In mathematics, hyperbolic space is a type of non-Euclidean geometry. Whereas spherical geometry has a constant positive curvature, hyperbolic geometry has a negative curvature: every point in hyperbolic space is a saddle point...
H3, and as orientation preserving conformal
Conformal map
In mathematics, a conformal map is a function which preserves angles. In the most common case the function is between domains in the complex plane.More formally, a map,...
maps of the open unit ball B3 in R3 to itself. Therefore a Kleinian group can be regarded as a discrete subgroup acting on one of these spaces.
There are some variations of the definition of a Kleinian group: sometimes
Kleinian groups are allowed to be subgroups of PSL(2, C).2 (PSL(2, C) extended by complex conjugations), in other words to have orientation reversing elements, and sometimes they are assumed to be finitely generated, and sometimes they are required to act properly discontinuously on a non-empty open subset of the Riemann sphere. A Kleinian group is said to be of type 1 if the limit set is the whole Riemann sphere, and of type 2 otherwise.
The theory of general Kleinian groups was founded by and , who named them after Felix Klein
Felix Klein
Christian Felix Klein was a German mathematician, known for his work in group theory, function theory, non-Euclidean geometry, and on the connections between geometry and group theory...
. The special case of Schottky group
Schottky group
In mathematics, a Schottky group is a special sort of Kleinian group, first studied by .-Definition:Fix some point p on the Riemann sphere...
s had been studied a few year before by Schottky.
Definitions
By considering the ball's boundary, a Kleinian group can also be defined as a subgroup Γ of PGL(2,C), the complex projective linear groupProjective linear group
In mathematics, especially in the group theoretic area of algebra, the projective linear group is the induced action of the general linear group of a vector space V on the associated projective space P...
, which acts by Möbius transformations on the Riemann sphere
Riemann sphere
In mathematics, the Riemann sphere , named after the 19th century mathematician Bernhard Riemann, is the sphere obtained from the complex plane by adding a point at infinity...
. Classically, a Kleinian group was required to act properly discontinuously on a non-empty open subset of the Riemann sphere, but modern usage allows any discrete subgroup.
When Γ is isomorphic to the fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
of a hyperbolic 3-manifoldHyperbolic 3-manifold
A hyperbolic 3-manifold is a 3-manifold equipped with a complete Riemannian metric of constant sectional curvature -1. In other words, it is the quotient of three-dimensional hyperbolic space by a subgroup of hyperbolic isometries acting freely and properly discontinuously...
, then the quotient space
Quotient space
In topology and related areas of mathematics, a quotient space is, intuitively speaking, the result of identifying or "gluing together" certain points of a given space. The points to be identified are specified by an equivalence relation...
H3/Γ becomes a Kleinian model of the manifold. Many authors use the terms Kleinian model and Kleinian group interchangeably, letting the one stand for the other.
Discreteness implies points in B3 have finite stabilizers, and discrete orbits under the group G. But the orbit Gp of a point p will typically accumulate on the boundary of the closed ball
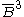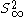.. The set of accumulation points of Gp in 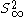is called the limit set of G, and usually denoted 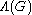. The complement 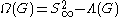is called the domain of discontinuity or the ordinary set or the regular set. Ahlfors' finiteness theorem implies that if the group is finitely generated then is a Riemann surface orbifold of finite type.The unit ball B3 with its conformal structure is the Poincaré model
Poincaré half-plane model
In non-Euclidean geometry, the Poincaré half-plane model is the upper half-plane , together with a metric, the Poincaré metric, that makes it a model of two-dimensional hyperbolic geometry....
of hyperbolic 3-space. When we think of it metrically, with metric
it is a model of 3-dimensional hyperbolic space H3. The set of conformal self-maps of B3 becomes the set of isometries (i.e. distance-preserving maps) of H3 under this identification. Such maps restrict to conformal self-maps of
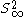, which are Möbius transformations. There are isomorphismsThe subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
s of these groups consisting of orientation-preserving transformations are all isomorphic to the projective matrix group: PSL(2,C) via the usual identification of the unit sphere
Unit sphere
In mathematics, a unit sphere is the set of points of distance 1 from a fixed central point, where a generalized concept of distance may be used; a closed unit ball is the set of points of distance less than or equal to 1 from a fixed central point...
with the complex projective line P1(C).
Finiteness conditions
- A Kleinian group is said to be of finite type if its region of discontinuity has a finite number of components, and the quotient of each component by its stabilizer is a compact Riemann surface with finitely many points removed, and the covering is ramified at finitely many points.
- A Kleinian group is called finitely generated if it has a finite number of generators. The Ahlfors finiteness theoremAhlfors finiteness theoremIn the mathematical theory of Kleinian groups, the Ahlfors finiteness theorem describes the quotient of the domain of discontinuity by a finitely generated Kleinian group...
says that such a group is of finite type. - A Kleinian group Γ has finite covolume if H3/Γ has finite volume. Any Kleinian group of finite covolume is finitely generated.
- A Kleinian group is called geometrically finite is it has a fundamental polyhedron (in hyperbolic 3-space) with finitely many sides. Ahlfors showed that if the limit set is not the whole Riemann sphere then it has measure 0.
- A Kleinian group Γ is called arithmetic if it is commensurable with the group of units of an order of quaternion algebra A ramified at all real places over a number field k with exactly one complex place. Arithmetic Kleinian groups have finite covolume.
- A Kleinian group Γ is called cocompact if H3/Γ is compact, or equivalently SL(2, C)/Γ is compact. Cocompact Kleinian groups have finite covolume.
- A Kleinian group is called topologically tame if it is finitely generated and its hyperbolic manifold is homeomorphic to the interior of a compact manifold with boundary.
- A Kleinian group is called geometrically tame if its ends are either geometrically finite or simply degenerate .
Bianchi groups
A Bianchi groupBianchi group
In mathematics, a Bianchi group is a group of the formwhere d is a positive square-free integer. Here, PSL denotes the projective special linear group and Od is the ring of integers of the imaginary quadratic field Q....
is a Kleinian group of the form PSL(2, Od), where d is a positive square-free integer
Square-free integer
In mathematics, a square-free, or quadratfrei, integer is one divisible by no perfect square, except 1. For example, 10 is square-free but 18 is not, as it is divisible by 9 = 32...
.
Elementary and reducible Kleinian groups
A Kleinian group is called degenerate if its limit set is finite, in which case the limit set has 0, 1, or 2 points.Examples of degenerate Kleinian groups include finite Kleinian groups (with empty limit set) and infinite cyclic Kleinian groups.
A Kleinian group is called reducible if all elements have a common fixed point on the Riemann sphere. Reducible Kleinian groups are elementary, but some elementary finite Kleinian groups are not reducible.
Fuchsian groups
Any Fuchsian groupFuchsian group
In mathematics, a Fuchsian group is a discrete subgroup of PSL. The group PSL can be regarded as a group of isometries of the hyperbolic plane, or conformal transformations of the unit disc, or conformal transformations of the upper half plane, so a Fuchsian group can be regarded as a group acting...
(a discrete subgroup of SL(2, R)) is a Kleinian group, and conversely any Kleinian group preserving the real line (in its action on the Riemann sphere) is a Fuchsian group. More generally, any Kleinian group preserving a circle or straight line in the Riemann sphere is conjugate to a Fuchsian group.
Koebe groups
- A factor of a Kleinian group G is a subgroup H maximal subject to the following properties:
- H has a simply connected invariant component D
- A conjugate of an element h of H by a conformal bijection is parabolic or elliptic if and only if h is.
- Any parabolic element of G fixing a boundary point of D is in H.
- A Kleinian group is called a Koebe group if all its factors are elementary or Fuchsian.
Quasi-Fuchsian groups
A Kleinian group that preserves a Jordan curve is called a quasi-Fuchsian groupQuasi-Fuchsian group
In the mathematical theory of Kleinian groups, a quasi-Fuchsian group is a Kleinian group whose limit set is contained in an invariant Jordan curve. If the limit set is equal to the Jordan curve the quasi-Fuchsian group is said to be of type one, and otherwise it is said to be of type two...
. When the Jordan curve is a circle or a straight line these are just conjugate to Fuchsian groups under conformal transformations. Finitely generated quasi-Fuchsian groups are conjugate to Fuchsian groups under quasi-conformal transformations. The limit set is contained in the invariant Jordan curve, and it is equal to the Jordan curve the group is said to be of type one, and otherwise it is said to be of type 2.
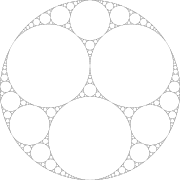
Schottky groups
Let Ci be the boundary circles of a finite collection of disjoint closed disks. The group generated by inversion in each circle has limit set a Cantor setCantor set
In mathematics, the Cantor set is a set of points lying on a single line segment that has a number of remarkable and deep properties. It was discovered in 1875 by Henry John Stephen Smith and introduced by German mathematician Georg Cantor in 1883....
, and the quotient H3/G is a mirror orbifold with underlying space a ball. It is double covered by a handlebody
Handlebody
In the mathematical field of geometric topology, a handlebody is a decomposition of a manifold into standard pieces. Handlebodies play an important role in Morse theory, cobordism theory and the surgery theory of high-dimensional manifolds...
; the corresponding index
Index of a subgroup
In mathematics, specifically group theory, the index of a subgroup H in a group G is the "relative size" of H in G: equivalently, the number of "copies" of H that fill up G. For example, if H has index 2 in G, then intuitively "half" of the elements of G lie in H...
2 subgroup is a Kleinian group called a Schottky group
Schottky group
In mathematics, a Schottky group is a special sort of Kleinian group, first studied by .-Definition:Fix some point p on the Riemann sphere...
.
Crystallographic groups
Let T be a periodicFrequency
Frequency is the number of occurrences of a repeating event per unit time. It is also referred to as temporal frequency.The period is the duration of one cycle in a repeating event, so the period is the reciprocal of the frequency...
tessellation
Tessellation
A tessellation or tiling of the plane is a pattern of plane figures that fills the plane with no overlaps and no gaps. One may also speak of tessellations of parts of the plane or of other surfaces. Generalizations to higher dimensions are also possible. Tessellations frequently appeared in the art...
of hyperbolic 3-space. The group of symmetries of the tessellation is a Kleinian group.
Fundamental groups of hyperbolic 3-manifolds
The fundamental group of any oriented hyperbolic 3-manifold is a Kleinian group. There are many examples of these, such as the complement of a figure 8 knot or the Seifert–Weber space. Conversely if a Kleinian group has no nontrivial torsion elements then it is the fundamental group of a hyperbolic 3-manifold.Degenerate Kleinian groups
A Kleinian group is called degenerate if it is not elementary and its limit set is simply connected. Such groups can be constructed by taking a suitable limit of quasi-Fuchsian groups such that one of the two components of the regular points contracts down to the empty set; these groups are called singly degenerate. If both components of the regular set contract down to the empty set, then the limit set becomes a space-filling curve and the group is called doubly degenerate.The existence of degenerate Kleinian groups was first shown indirectly by , and the first explicit example was found by Jørgensen. gave examples of doubly degenerate groups and space-filling curves associated to pseudo-Anosov map
Pseudo-Anosov map
In mathematics, specifically in topology, a pseudo-Anosov map is a type of a diffeomorphism or homeomorphism of a surface. It is a generalization of a linear Anosov diffeomorphism of the torus...
s.
See also
- Tameness theorem (Marden's conjecture)
- Ahlfors measure conjectureAhlfors measure conjectureIn mathematics, the Ahlfors conjecture, now a theorem, states that the limit set of a finitely-generated Kleinian group is either the whole Riemann sphere, or has measure 0....
- density theorem for Kleinian groupsDensity theorem for Kleinian groupsIn the mathematical theory of Kleinian groups, the density conjecture of Lipman Bers, Dennis Sullivan, and William Thurston, states that every finitely generated Kleinian group is an algebraic limit of geometrically finite Kleinian groups.-History:...
- Ending lamination theoremEnding lamination theoremIn hyperbolic geometry, the ending lamination theorem, originally conjectured by , states that hyperbolic 3-manifolds with finitely generated fundamental groups are determined by their topology together with certain "end invariants", which are geodesic laminations on some surfaces in the boundary...
External links
- A picture of the limit set of a quasi-Fuchsian group from .
- A picture of the limit set of a Kleinian group from . This was one of the first pictures of a limit set. A computer drawing of the same limit set
- Images of limit sets of Kleinian groups on google
- Animations of Kleinian group limit sets
- Images related to Kleinian groups by McMullen
- A program for drawing pictures related to Kleinian groups, by David Wright.