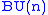Classifying space
Encyclopedia
In mathematics
, specifically in homotopy theory, a classifying space BG of a topological group
G is the quotient of a weakly contractible
space EG (i.e. a topological space for which all its homotopy group
s are trivial) by a free action of G. It has the property that any G principal bundle
over a paracompact manifold is isomorphic to a pullback
of the principal bundle
For a discrete group
G, BG is, roughly speaking, a path-connected
topological space
X such that the fundamental group
of X is isomorphic to G and the higher homotopy groups of X are trivial
, that is, BG is an Eilenberg-Maclane space
, or a K(G,1).
as X. When G is a discrete group
, another way to specify the condition on X is that the universal cover Y of X is contractible. In that case the projection map
becomes a fiber bundle
with structure group G, in fact a principal bundle
for G. The interest in the classifying space concept really arises from the fact that in this case Y has a universal property
with respect to principal G-bundles, in the homotopy category. This is actually more basic than the condition that the higher homotopy groups vanish: the fundamental idea is, given G, to find such a contractible space Y on which G acts freely
. (The weak equivalence
idea of homotopy theory relates the two versions.) In the case of the circle example, what is being said is that we remark that an infinite cyclic group C acts freely on the real line
R, which is contractible. Taking X as the quotient space
circle, we can regard the projection π from R = Y to X as a helix
in geometrical terms, undergoing projection from three dimensions to the plane. What is being claimed is that π has a universal property amongst principal C-bundles; that any principal C-bundle in a definite way 'comes from' π.
(not simply a discrete group), and that group action
s of G are taken to be continuous; in the absence of continuous actions the classifying space concept can be dealt with, in homotopy terms, via the Eilenberg–MacLane space construction. In homotopy theory the definition of a topological space BG, the classifying space for principal G-bundles, is given, together with the space EG which is the total space of the universal bundle
over BG. That is, what is provided is in fact a continuous mapping
Assume that the homotopy category of CW complex
es is the underlying category, from now on. The classifying property required of BG in fact relates to π. We must be able to say that given any principal G-bundle
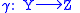
over a space Z, there is a classifying map φ from Z to BG, such that γ is the pullback of a bundle of π along φ. In less abstract terms, the construction of γ by 'twisting' should be reducible via φ to the twisting already expressed by the construction of π.
For this to be a useful concept, there evidently must be some reason to believe such spaces BG exist. In abstract terms (which are not those originally used around 1950 when the idea was first introduced) this is a question of whether the contravariant functor from the homotopy category to the category of sets
, defined by
is a representable functor
. The abstract conditions being known for this (Brown's representability theorem
) the result, as an existence theorem
, is affirmative and not too difficult.
es is essentially the same as computing the cohomology groups of BG, at least within the restrictive terms of homotopy theory, for interesting groups G such as Lie group
s. As was shown by the Bott periodicity theorem
, the homotopy group
s of BG are also of fundamental interest. The early work on classifying spaces introduced constructions (for example, the bar construction), that gave concrete descriptions as a simplicial complex
.
An example of a classifying space is that when G is cyclic of order two; then BG is real projective space
of infinite dimension, corresponding to the observation that EG can be taken as the contractible space resulting from removing the origin in an infinite-dimensional Hilbert space
, with G acting via v going to −v, and allowing for homotopy equivalence in choosing BG. This example shows that classifying spaces may be complicated.
In relation with differential geometry (Chern–Weil theory) and the theory of Grassmannian
s, a much more hands-on approach to the theory is possible for cases such as the unitary group
s that are of greatest interest. The construction of the Thom complex MG showed that the spaces BG were also implicated in cobordism theory, so that they assumed a central place in geometric considerations coming out of algebraic topology
. Since group cohomology
can (in many cases) be defined by the use of classifying spaces, they can also be seen as foundational in much homological algebra
.
Generalizations include those for classifying foliation
s, and the classifying toposes for logical theories of the predicate calculus in intuitionistic logic
that take the place of a 'space of models'.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, specifically in homotopy theory, a classifying space BG of a topological group
Topological group
In mathematics, a topological group is a group G together with a topology on G such that the group's binary operation and the group's inverse function are continuous functions with respect to the topology. A topological group is a mathematical object with both an algebraic structure and a...
G is the quotient of a weakly contractible
Weakly contractible
In mathematics, a topological space is said to be weakly contractible if all of its homotopy groups are trivial.-Property:It follows from Whitehead's Theorem that if a CW-complex is weakly contractible then it is contractible.-Example:...
space EG (i.e. a topological space for which all its homotopy group
Homotopy group
In mathematics, homotopy groups are used in algebraic topology to classify topological spaces. The first and simplest homotopy group is the fundamental group, which records information about loops in a space...
s are trivial) by a free action of G. It has the property that any G principal bundle
Principal bundle
In mathematics, a principal bundle is a mathematical object which formalizes some of the essential features of the Cartesian product X × G of a space X with a group G...
over a paracompact manifold is isomorphic to a pullback
Pullback bundle
In mathematics, a pullback bundle or induced bundle is a useful construction in the theory of fiber bundles. Given a fiber bundle π : E → B and a continuous map f : B′ → B one can define a "pullback" of E by f as a bundle f*E over B′...
of the principal bundle
For a discrete group
Discrete group
In mathematics, a discrete group is a group G equipped with the discrete topology. With this topology G becomes a topological group. A discrete subgroup of a topological group G is a subgroup H whose relative topology is the discrete one...
G, BG is, roughly speaking, a path-connected
Connected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
X such that the fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
of X is isomorphic to G and the higher homotopy groups of X are trivial
Trivial group
In mathematics, a trivial group is a group consisting of a single element. All such groups are isomorphic so one often speaks of the trivial group. The single element of the trivial group is the identity element so it usually denoted as such, 0, 1 or e depending on the context...
, that is, BG is an Eilenberg-Maclane space
Eilenberg-MacLane space
In mathematics, an Eilenberg–MacLane spaceSaunders Mac Lane originally spelt his name "MacLane" , and co-published the papers establishing the notion of Eilenberg–MacLane spaces under this name. In mathematics, an Eilenberg–MacLane spaceSaunders Mac Lane originally spelt his name "MacLane" (without...
, or a K(G,1).
Motivation
An example for G infinite cyclic is the circleCircle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
as X. When G is a discrete group
Discrete group
In mathematics, a discrete group is a group G equipped with the discrete topology. With this topology G becomes a topological group. A discrete subgroup of a topological group G is a subgroup H whose relative topology is the discrete one...
, another way to specify the condition on X is that the universal cover Y of X is contractible. In that case the projection map
becomes a fiber bundle
Fiber bundle
In mathematics, and particularly topology, a fiber bundle is intuitively a space which locally "looks" like a certain product space, but globally may have a different topological structure...
with structure group G, in fact a principal bundle
Principal bundle
In mathematics, a principal bundle is a mathematical object which formalizes some of the essential features of the Cartesian product X × G of a space X with a group G...
for G. The interest in the classifying space concept really arises from the fact that in this case Y has a universal property
Universal property
In various branches of mathematics, a useful construction is often viewed as the “most efficient solution” to a certain problem. The definition of a universal property uses the language of category theory to make this notion precise and to study it abstractly.This article gives a general treatment...
with respect to principal G-bundles, in the homotopy category. This is actually more basic than the condition that the higher homotopy groups vanish: the fundamental idea is, given G, to find such a contractible space Y on which G acts freely
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
. (The weak equivalence
Weak equivalence
-Mathematics:In mathematics, a weak equivalence is a notion from homotopy theory which in some sense identifies objects that have the same basic "shape"...
idea of homotopy theory relates the two versions.) In the case of the circle example, what is being said is that we remark that an infinite cyclic group C acts freely on the real line
Real line
In mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
R, which is contractible. Taking X as the quotient space
Quotient space
In topology and related areas of mathematics, a quotient space is, intuitively speaking, the result of identifying or "gluing together" certain points of a given space. The points to be identified are specified by an equivalence relation...
circle, we can regard the projection π from R = Y to X as a helix
Helix
A helix is a type of smooth space curve, i.e. a curve in three-dimensional space. It has the property that the tangent line at any point makes a constant angle with a fixed line called the axis. Examples of helixes are coil springs and the handrails of spiral staircases. A "filled-in" helix – for...
in geometrical terms, undergoing projection from three dimensions to the plane. What is being claimed is that π has a universal property amongst principal C-bundles; that any principal C-bundle in a definite way 'comes from' π.
Formalism
A more formal statement takes into account that G may be a topological groupTopological group
In mathematics, a topological group is a group G together with a topology on G such that the group's binary operation and the group's inverse function are continuous functions with respect to the topology. A topological group is a mathematical object with both an algebraic structure and a...
(not simply a discrete group), and that group action
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
s of G are taken to be continuous; in the absence of continuous actions the classifying space concept can be dealt with, in homotopy terms, via the Eilenberg–MacLane space construction. In homotopy theory the definition of a topological space BG, the classifying space for principal G-bundles, is given, together with the space EG which is the total space of the universal bundle
Universal bundle
In mathematics, the universal bundle in the theory of fiber bundles with structure group a given topological group G, is a specific bundle over a classifying space BG, such that every bundle with the given structure group G over M is a pullback by means of a continuous map-In the CW complex...
over BG. That is, what is provided is in fact a continuous mapping
Assume that the homotopy category of CW complex
CW complex
In topology, a CW complex is a type of topological space introduced by J. H. C. Whitehead to meet the needs of homotopy theory. This class of spaces is broader and has some better categorical properties than simplicial complexes, but still retains a combinatorial naturethat allows for...
es is the underlying category, from now on. The classifying property required of BG in fact relates to π. We must be able to say that given any principal G-bundle
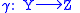
over a space Z, there is a classifying map φ from Z to BG, such that γ is the pullback of a bundle of π along φ. In less abstract terms, the construction of γ by 'twisting' should be reducible via φ to the twisting already expressed by the construction of π.
For this to be a useful concept, there evidently must be some reason to believe such spaces BG exist. In abstract terms (which are not those originally used around 1950 when the idea was first introduced) this is a question of whether the contravariant functor from the homotopy category to the category of sets
Category of sets
In the mathematical field of category theory, the category of sets, denoted as Set, is the category whose objects are sets. The arrows or morphisms between sets A and B are all functions from A to B...
, defined by
- h(Z) = set of isomorphism classes of principal G-bundles on Z
is a representable functor
Representable functor
In mathematics, particularly category theory, a representable functor is a functor of a special form from an arbitrary category into the category of sets. Such functors give representations of an abstract category in terms of known structures In mathematics, particularly category theory, a...
. The abstract conditions being known for this (Brown's representability theorem
Brown's representability theorem
In mathematics, Brown's representability theorem in homotopy theory gives necessary and sufficient conditions on a contravariant functor F on the homotopy category Hot of pointed CW complexes, to the category of sets Set, to be a representable functor...
) the result, as an existence theorem
Existence theorem
In mathematics, an existence theorem is a theorem with a statement beginning 'there exist ..', or more generally 'for all x, y, ... there exist ...'. That is, in more formal terms of symbolic logic, it is a theorem with a statement involving the existential quantifier. Many such theorems will not...
, is affirmative and not too difficult.
Examples
- The circleCircleA circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
is a classifying space for the infinite cyclic group 
. - The n-torusTorusIn geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
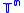is a classifying space for 
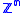, the free abelian groupFree abelian groupIn abstract algebra, a free abelian group is an abelian group that has a "basis" in the sense that every element of the group can be written in one and only one way as a finite linear combination of elements of the basis, with integer coefficients. Hence, free abelian groups over a basis B are...
of rank n. - The wedge of n circles is a classifying space for the free groupFree groupIn mathematics, a group G is called free if there is a subset S of G such that any element of G can be written in one and only one way as a product of finitely many elements of S and their inverses...
of rank n. - A closedClosed manifoldIn mathematics, a closed manifold is a type of topological space, namely a compact manifold without boundary. In contexts where no boundary is possible, any compact manifold is a closed manifold....
(that is compactCompact spaceIn mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
and without boundary) connected surfaceSurfaceIn mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...
S of genusGenus (mathematics)In mathematics, genus has a few different, but closely related, meanings:-Orientable surface:The genus of a connected, orientable surface is an integer representing the maximum number of cuttings along non-intersecting closed simple curves without rendering the resultant manifold disconnected. It...
at least 1 is a classifying space for its fundamental groupFundamental groupIn mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
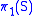. - The infinite-dimensional real projective space
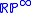is a classifying space for 
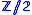. - A closedClosed manifoldIn mathematics, a closed manifold is a type of topological space, namely a compact manifold without boundary. In contexts where no boundary is possible, any compact manifold is a closed manifold....
(that is compactCompact spaceIn mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
and without boundary) connected hyperbolic manifoldHyperbolic manifoldIn mathematics, a hyperbolic n-manifold is a complete Riemannian n-manifold of constant sectional curvature -1.Every complete, connected, simply-connected manifold of constant negative curvature −1 is isometric to the real hyperbolic space Hn. As a result, the universal cover of any closed manifold...
M is a classifying space for its fundamental groupFundamental groupIn mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
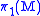. - A finite connected locally CAT(0) cubical complex is a classifying space of its fundamental groupFundamental groupIn mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
.
Applications
This still leaves the question of doing effective calculations with BG; for example, the theory of characteristic classCharacteristic class
In mathematics, a characteristic class is a way of associating to each principal bundle on a topological space X a cohomology class of X. The cohomology class measures the extent to which the bundle is "twisted" — particularly, whether it possesses sections or not...
es is essentially the same as computing the cohomology groups of BG, at least within the restrictive terms of homotopy theory, for interesting groups G such as Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
s. As was shown by the Bott periodicity theorem
Bott periodicity theorem
In mathematics, the Bott periodicity theorem describes a periodicity in the homotopy groups of classical groups, discovered by , which proved to be of foundational significance for much further research, in particular in K-theory of stable complex vector bundles, as well as the stable homotopy...
, the homotopy group
Homotopy group
In mathematics, homotopy groups are used in algebraic topology to classify topological spaces. The first and simplest homotopy group is the fundamental group, which records information about loops in a space...
s of BG are also of fundamental interest. The early work on classifying spaces introduced constructions (for example, the bar construction), that gave concrete descriptions as a simplicial complex
Simplicial complex
In mathematics, a simplicial complex is a topological space of a certain kind, constructed by "gluing together" points, line segments, triangles, and their n-dimensional counterparts...
.
An example of a classifying space is that when G is cyclic of order two; then BG is real projective space
Real projective space
In mathematics, real projective space, or RPn, is the topological space of lines through 0 in Rn+1. It is a compact, smooth manifold of dimension n, and a special case of a Grassmannian.-Construction:...
of infinite dimension, corresponding to the observation that EG can be taken as the contractible space resulting from removing the origin in an infinite-dimensional Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
, with G acting via v going to −v, and allowing for homotopy equivalence in choosing BG. This example shows that classifying spaces may be complicated.
In relation with differential geometry (Chern–Weil theory) and the theory of Grassmannian
Grassmannian
In mathematics, a Grassmannian is a space which parameterizes all linear subspaces of a vector space V of a given dimension. For example, the Grassmannian Gr is the space of lines through the origin in V, so it is the same as the projective space P. The Grassmanians are compact, topological...
s, a much more hands-on approach to the theory is possible for cases such as the unitary group
Unitary group
In mathematics, the unitary group of degree n, denoted U, is the group of n×n unitary matrices, with the group operation that of matrix multiplication. The unitary group is a subgroup of the general linear group GL...
s that are of greatest interest. The construction of the Thom complex MG showed that the spaces BG were also implicated in cobordism theory, so that they assumed a central place in geometric considerations coming out of algebraic topology
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
. Since group cohomology
Group cohomology
In abstract algebra, homological algebra, algebraic topology and algebraic number theory, as well as in applications to group theory proper, group cohomology is a way to study groups using a sequence of functors H n. The study of fixed points of groups acting on modules and quotient modules...
can (in many cases) be defined by the use of classifying spaces, they can also be seen as foundational in much homological algebra
Homological algebra
Homological algebra is the branch of mathematics which studies homology in a general algebraic setting. It is a relatively young discipline, whose origins can be traced to investigations in combinatorial topology and abstract algebra at the end of the 19th century, chiefly by Henri Poincaré and...
.
Generalizations include those for classifying foliation
Foliation
In mathematics, a foliation is a geometric device used to study manifolds, consisting of an integrable subbundle of the tangent bundle. A foliation looks locally like a decomposition of the manifold as a union of parallel submanifolds of smaller dimension....
s, and the classifying toposes for logical theories of the predicate calculus in intuitionistic logic
Intuitionistic logic
Intuitionistic logic, or constructive logic, is a symbolic logic system differing from classical logic in its definition of the meaning of a statement being true. In classical logic, all well-formed statements are assumed to be either true or false, even if we do not have a proof of either...
that take the place of a 'space of models'.
See also
- Classifying space for O(n)Classifying space for O(n)In mathematics, the classifying space for O may be constructed as the Grassmannian of n-planes in an infinite-dimensional real Hilbert space.It is analogous to the classifying space for U....
,
- Classifying space for U(n)Classifying space for U(n)In mathematics, the classifying space for the unitary group U is a space B together with a universal bundle E such that any hermitian bundle on a paracompact space X is the pull-back of E by a map X → B unique up to homotopy.This space with its universal fibration may be constructed as either# the...
,