
Unitary group
Encyclopedia
In mathematics
, the unitary group of degree n, denoted U(n), is the group
of n×n unitary matrices, with the group operation that of matrix multiplication
. The unitary group is a subgroup
of the general linear group
GL(n, C). Hyperorthogonal group is an archaic name for the unitary group, especially over finite fields.
In the simple case n = 1, the group U(1) corresponds to the circle group, consisting of all complex numbers with absolute value 1 under multiplication. All the unitary groups contain copies of this group.
The unitary group U(n) is a real Lie group
of dimension n2. The Lie algebra
of U(n) consists of complex n×n skew-Hermitian matrices
, with the Lie bracket
given by the commutator
.
The general unitary group (also called the group of unitary similitudes) consists of all matrices such that
such that
 is a nonzero multiple of the identity matrix
is a nonzero multiple of the identity matrix
, and is just the product of the unitary group with the group of all positive multiples of the identity matrix.
of a unitary matrix is a complex number with norm 1, the determinant gives a group homomorphism

The kernel of this homomorphism is the set of unitary matrices with determinant 1. This subgroup is called the special unitary group
, denoted SU(n). We then have a short exact sequence of Lie groups:
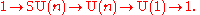
This short exact sequence splits so that U(n) may be written as a semidirect product
of SU(n) by U(1). Here the U(1) subgroup of U(n) consists of matrices of the form diag(eiθ, 1, 1, ..., 1).
The unitary group U(n) is nonabelian
for n > 1. The center of U(n) is the set of scalar matrices λI with λ ∈ U(1). This follows from Schur's lemma
. The center is then isomorphic to U(1). Since the center of U(n) is a 1-dimensional abelian normal subgroup
of U(n), the unitary group is not semisimple
.
.
As a topological space, U(n) is both compact
and connected
. The compactness of U(n) follows from the Heine-Borel theorem and the fact that it is a closed and bounded subset of Mn(C). To show that U(n) is connected, recall that any unitary matrix A can be diagonalized by another unitary matrix S. Any diagonal unitary matrix must have complex numbers of absolute value 1 on the main diagonal. We can therefore write
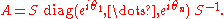
A path
in U(n) from the identity to A is then given by
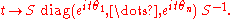
The unitary group is not simply connected; the fundamental group of U(n) is infinite cyclic for all n:
The first unitary group U(1) is topologically a circle
, which is well known to have a fundamental group
isomorphic to Z, and the inclusion map is an isomorphism on
is an isomorphism on  .
.
(It has quotient the Stiefel manifold
.)
The determinant map induces an isomorphism of fundamental groups, with the splitting
induces an isomorphism of fundamental groups, with the splitting  inducing the inverse.
inducing the inverse.
, symplectic
, and complex groups:
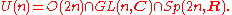
Thus a unitary structure can be seen as an orthogonal structure, a complex structure, and a symplectic structure, which are required to be compatible (meaning that one uses the same J in the complex structure and the symplectic form, and that this J is orthogonal; writing all the groups as matrix groups fixes a J (which is orthogonal) and ensures compatibility).
In fact, it is the intersection of any two of these three; thus a compatible orthogonal and complex structure induce a symplectic structure, and so forth.
At the level of equations, this can be seen as follows:
Any two of these equations implies the third.
At the level of forms, this can be seen by decomposing a Hermitian form into its real and imaginary parts:
the real part is symmetric (orthogonal), and the imaginary part is skew-symmetric (symplectic)—and these are related by the complex structure (which is the compatibility). On an almost Kähler manifold, one can write this decomposition as , where h is the Hermitian form, g is the Riemannian metric, i is the almost complex structure
, where h is the Hermitian form, g is the Riemannian metric, i is the almost complex structure
, and is the almost symplectic structure
is the almost symplectic structure
.
From the point of view of Lie group
s, this can partly be explained as follows:
 is the maximal compact subgroup
is the maximal compact subgroup
of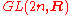 , and
, and 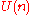 is the maximal compact subgroup of both
is the maximal compact subgroup of both 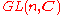 and
and 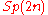 . Thus the intersection of
. Thus the intersection of  or
or 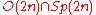 is the maximal compact subgroup of both of these, so
is the maximal compact subgroup of both of these, so  . From this perspective, what is unexpected is the intersection
. From this perspective, what is unexpected is the intersection 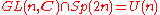 .
.
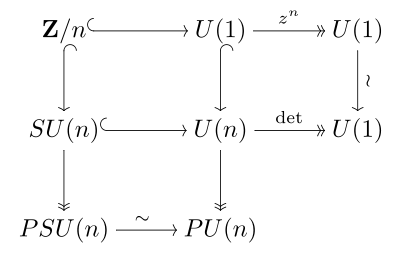
Just as the orthogonal group has the special orthogonal group SO(n) as subgroup and the projective orthogonal group
PO(n) as quotient, and the projective special orthogonal group PSO(n) as subquotient
, the unitary group has associated to it the special unitary group
SU(n), the projective unitary group
PU(n), and the projective special unitary group PSU(n). These are related as by the commutative diagram at right; notably, both projective groups are equal: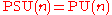 .
.
The above is for the classical unitary group (over the complex numbers) – for unitary groups over finite fields, one similarly obtains special unitary and projective unitary groups, but in general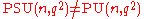 .
.
s, a manifold with a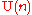 -structure is an almost Hermitian manifold.
-structure is an almost Hermitian manifold.
, the classical unitary group is a real form of the Steinberg group , which is an algebraic group
, which is an algebraic group
that arises from the combination of the diagram automorphism of the general linear group (reversing the Dynkin diagram , which corresponds to transpose inverse) and the field automorphism of the extension
, which corresponds to transpose inverse) and the field automorphism of the extension 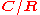 (namely complex conjugation). Both these automorphisms are automorphisms of the algebraic group, have order 2, and commute, and the unitary group is the fixed points of the product automorphism, as an algebraic group.
(namely complex conjugation). Both these automorphisms are automorphisms of the algebraic group, have order 2, and commute, and the unitary group is the fixed points of the product automorphism, as an algebraic group.
The classical unitary group is a real form of this group, corresponding to the standard Hermitian form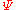 , which is positive definite.
, which is positive definite.
This can be generalized in a number of ways:
Given a Hermitian form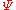 on a complex vector space
on a complex vector space  , the unitary group
, the unitary group 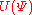 is the group of transforms that preserve the form: the transform
is the group of transforms that preserve the form: the transform  such that
such that 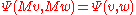 for all
for all  . In terms of matrices, representing the form by a matrix denoted
. In terms of matrices, representing the form by a matrix denoted  , this says that
, this says that 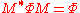 .
.
Just as for symmetric forms over the reals, Hermitian forms are determined by signature, and are all unitarily congruent
to a diagonal form with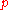 entries of 1 on the diagonal and
entries of 1 on the diagonal and 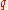 entries of
entries of 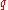 . The non-degenerate assumption is equivalent to
. The non-degenerate assumption is equivalent to 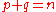 . In a standard basis, this is represented as a quadratic form as:
. In a standard basis, this is represented as a quadratic form as: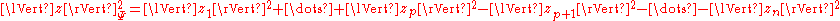
and as a symmetric form as: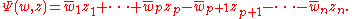
The resulting group is denoted .
.
with elements,
elements, 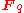 , there is a unique degree 2 extension field,
, there is a unique degree 2 extension field, 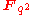 , with order 2 automorphism
, with order 2 automorphism 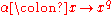 (the
(the  th power of the Frobenius automorphism). This allows one to define a Hermitian form on an
th power of the Frobenius automorphism). This allows one to define a Hermitian form on an 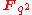 vector space
vector space  , as an
, as an 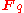 -bilinear map
-bilinear map 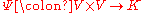 such that
such that 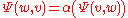 and
and  for
for  .
.
Further, all non-degenerate Hermitian forms on a vector space over a finite field are unitarily congruent to the standard one, represented by the identity matrix, that is, any Hermitian form is unitarily equivalent to
where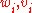 represent the coordinates of
represent the coordinates of 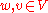 in some particular
in some particular 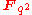 -basis of the
-basis of the  -dimensional space
-dimensional space  .
.
Thus one can define a (unique) unitary group of dimension for the extension
for the extension 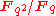 , denoted either as
, denoted either as 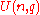 or
or 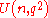 depending on the author. The subgroup of the unitary group consisting of matrices of determinant 1 is called the special unitary group and denoted
depending on the author. The subgroup of the unitary group consisting of matrices of determinant 1 is called the special unitary group and denoted 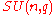 or
or  . For convenience, this article will use the
. For convenience, this article will use the 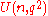 convention. The center of
convention. The center of 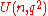 has order
has order  and consists of the scalar matrices which are unitary, that is those matrices
and consists of the scalar matrices which are unitary, that is those matrices 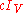 with
with  . The center of the special unitary group has order
. The center of the special unitary group has order 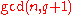 and consists of those unitary scalars which also have order dividing
and consists of those unitary scalars which also have order dividing  . The quotient of the unitary group by its center is called the projective unitary group
. The quotient of the unitary group by its center is called the projective unitary group
,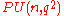 , and the quotient of the special unitary group by its center is the projective special unitary group
, and the quotient of the special unitary group by its center is the projective special unitary group 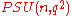 . In most cases (
. In most cases ( and
and  ),
),  is a perfect group
is a perfect group
and is a finite simple group
is a finite simple group
, .
one can define unitary groups with respect to this extension.
First, there is a unique k-automorphism of K which is an involution and fixes exactly
which is an involution and fixes exactly 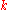 (
( if and only if
if and only if  ). This generalizes complex conjugation and the conjugation of degree 2 finite field extensions, and allows one to define Hermitian forms and unitary groups as above.
). This generalizes complex conjugation and the conjugation of degree 2 finite field extensions, and allows one to define Hermitian forms and unitary groups as above.
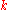 (but not over
(but not over  ): for the standard form
): for the standard form  the equations are given in matrices as
the equations are given in matrices as 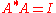 , where
, where  is the conjugate transpose
is the conjugate transpose
. Given a different form, they are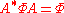 . The unitary group is thus an algebraic group
. The unitary group is thus an algebraic group
, whose points over a -algebra
-algebra  are given by:
are given by: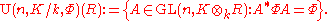
For the field extension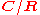 and the standard (positive definite) Hermitian form, these yield an algebraic group with real and complex points given by:
and the standard (positive definite) Hermitian form, these yield an algebraic group with real and complex points given by: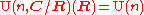
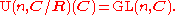

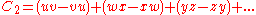
These are easily seen to be the real and imginary parts of the complex form . The two invariants separately are invariants of O(2n) and Sp(2n,R). Combined they make the invariants of U(n) which is a subgroup of both these groups. The variables must be non-commutative in these invariants otherwise the second polynomial is identically zero.
. The two invariants separately are invariants of O(2n) and Sp(2n,R). Combined they make the invariants of U(n) which is a subgroup of both these groups. The variables must be non-commutative in these invariants otherwise the second polynomial is identically zero.
for U(n) is described in the article classifying space for U(n)
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the unitary group of degree n, denoted U(n), is the group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
of n×n unitary matrices, with the group operation that of matrix multiplication
Matrix multiplication
In mathematics, matrix multiplication is a binary operation that takes a pair of matrices, and produces another matrix. If A is an n-by-m matrix and B is an m-by-p matrix, the result AB of their multiplication is an n-by-p matrix defined only if the number of columns m of the left matrix A is the...
. The unitary group is a subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
of the general linear group
General linear group
In mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible...
GL(n, C). Hyperorthogonal group is an archaic name for the unitary group, especially over finite fields.
In the simple case n = 1, the group U(1) corresponds to the circle group, consisting of all complex numbers with absolute value 1 under multiplication. All the unitary groups contain copies of this group.
The unitary group U(n) is a real Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
of dimension n2. The Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
of U(n) consists of complex n×n skew-Hermitian matrices
Skew-Hermitian matrix
In linear algebra, a square matrix with complex entries is said to be skew-Hermitian or antihermitian if its conjugate transpose is equal to its negative. That is, the matrix A is skew-Hermitian if it satisfies the relationA^\dagger = -A,\;...
, with the Lie bracket
Lie bracket
Lie bracket can refer to:*A bilinear binary operation defined on elements of a Lie algebra*Lie bracket of vector fields...
given by the commutator
Commutator
In mathematics, the commutator gives an indication of the extent to which a certain binary operation fails to be commutative. There are different definitions used in group theory and ring theory.-Group theory:...
.
The general unitary group (also called the group of unitary similitudes) consists of all matrices
 such that
such that is a nonzero multiple of the identity matrix
is a nonzero multiple of the identity matrixIdentity matrix
In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
, and is just the product of the unitary group with the group of all positive multiples of the identity matrix.
Properties
Since the determinantDeterminant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
of a unitary matrix is a complex number with norm 1, the determinant gives a group homomorphism
Group homomorphism
In mathematics, given two groups and , a group homomorphism from to is a function h : G → H such that for all u and v in G it holds that h = h \cdot h...

The kernel of this homomorphism is the set of unitary matrices with determinant 1. This subgroup is called the special unitary group
Special unitary group
The special unitary group of degree n, denoted SU, is the group of n×n unitary matrices with determinant 1. The group operation is that of matrix multiplication...
, denoted SU(n). We then have a short exact sequence of Lie groups:
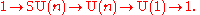
This short exact sequence splits so that U(n) may be written as a semidirect product
Semidirect product
In mathematics, specifically in the area of abstract algebra known as group theory, a semidirect product is a particular way in which a group can be put together from two subgroups, one of which is a normal subgroup. A semidirect product is a generalization of a direct product...
of SU(n) by U(1). Here the U(1) subgroup of U(n) consists of matrices of the form diag(eiθ, 1, 1, ..., 1).
The unitary group U(n) is nonabelian
Nonabelian group
In mathematics, a non-abelian group, also sometimes called a non-commutative group, is a group in which there are at least two elements a and b of G such that a * b ≠ b * a...
for n > 1. The center of U(n) is the set of scalar matrices λI with λ ∈ U(1). This follows from Schur's lemma
Schur's lemma
In mathematics, Schur's lemma is an elementary but extremely useful statement in representation theory of groups and algebras. In the group case it says that if M and N are two finite-dimensional irreducible representations...
. The center is then isomorphic to U(1). Since the center of U(n) is a 1-dimensional abelian normal subgroup
Normal subgroup
In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
of U(n), the unitary group is not semisimple
Semisimple
In mathematics, the term semisimple is used in a number of related ways, within different subjects. The common theme is the idea of a decomposition into 'simple' parts, that fit together in the cleanest way...
.
Topology
The unitary group U(n) is endowed with the relative topology as a subset of Mn(C), the set of all n×n complex matrices, which is itself homeomorphic to a 2n2-dimensional Euclidean spaceEuclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
.
As a topological space, U(n) is both compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
and connected
Connected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
. The compactness of U(n) follows from the Heine-Borel theorem and the fact that it is a closed and bounded subset of Mn(C). To show that U(n) is connected, recall that any unitary matrix A can be diagonalized by another unitary matrix S. Any diagonal unitary matrix must have complex numbers of absolute value 1 on the main diagonal. We can therefore write
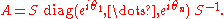
A path
Path (topology)
In mathematics, a path in a topological space X is a continuous map f from the unit interval I = [0,1] to XThe initial point of the path is f and the terminal point is f. One often speaks of a "path from x to y" where x and y are the initial and terminal points of the path...
in U(n) from the identity to A is then given by
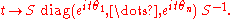
The unitary group is not simply connected; the fundamental group of U(n) is infinite cyclic for all n:

The first unitary group U(1) is topologically a circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
, which is well known to have a fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
isomorphic to Z, and the inclusion map
 is an isomorphism on
is an isomorphism on  .
.(It has quotient the Stiefel manifold
Stiefel manifold
In mathematics, the Stiefel manifold Vk is the set of all orthonormal k-frames in Rn. That is, it is the set of ordered k-tuples of orthonormal vectors in Rn. It is named after Swiss mathematician Eduard Stiefel...
.)
The determinant map
 induces an isomorphism of fundamental groups, with the splitting
induces an isomorphism of fundamental groups, with the splitting  inducing the inverse.
inducing the inverse.2-out-of-3 property
The unitary group is the 3-fold intersection of the orthogonalOrthogonal group
In mathematics, the orthogonal group of degree n over a field F is the group of n × n orthogonal matrices with entries from F, with the group operation of matrix multiplication...
, symplectic
Symplectic group
In mathematics, the name symplectic group can refer to two different, but closely related, types of mathematical groups, denoted Sp and Sp. The latter is sometimes called the compact symplectic group to distinguish it from the former. Many authors prefer slightly different notations, usually...
, and complex groups:
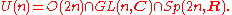
Thus a unitary structure can be seen as an orthogonal structure, a complex structure, and a symplectic structure, which are required to be compatible (meaning that one uses the same J in the complex structure and the symplectic form, and that this J is orthogonal; writing all the groups as matrix groups fixes a J (which is orthogonal) and ensures compatibility).
In fact, it is the intersection of any two of these three; thus a compatible orthogonal and complex structure induce a symplectic structure, and so forth.
At the level of equations, this can be seen as follows:
- Symplectic:
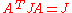
- Complex:
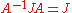
- Orthogonal:
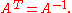
Any two of these equations implies the third.
At the level of forms, this can be seen by decomposing a Hermitian form into its real and imaginary parts:
the real part is symmetric (orthogonal), and the imaginary part is skew-symmetric (symplectic)—and these are related by the complex structure (which is the compatibility). On an almost Kähler manifold, one can write this decomposition as
 , where h is the Hermitian form, g is the Riemannian metric, i is the almost complex structure
, where h is the Hermitian form, g is the Riemannian metric, i is the almost complex structureAlmost complex manifold
In mathematics, an almost complex manifold is a smooth manifold equipped with smooth linear complex structure on each tangent space. The existence of this structure is a necessary, but not sufficient, condition for a manifold to be a complex manifold. That is, every complex manifold is an almost...
, and
 is the almost symplectic structure
is the almost symplectic structureAlmost symplectic manifold
In differential geometry, an almost symplectic structure on a differentiable manifold M is a two-form ω on M which is everywhere non-singular. If, in addition, ω is closed, then it is a symplectic form....
.
From the point of view of Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
s, this can partly be explained as follows:
 is the maximal compact subgroup
is the maximal compact subgroupMaximal compact subgroup
In mathematics, a maximal compact subgroup K of a topological group G is a subgroup K that is a compact space, in the subspace topology, and maximal amongst such subgroups....
of
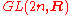 , and
, and 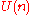 is the maximal compact subgroup of both
is the maximal compact subgroup of both 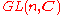 and
and 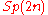 . Thus the intersection of
. Thus the intersection of  or
or 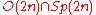 is the maximal compact subgroup of both of these, so
is the maximal compact subgroup of both of these, so  . From this perspective, what is unexpected is the intersection
. From this perspective, what is unexpected is the intersection 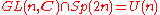 .
.Special unitary and projective unitary groups

Just as the orthogonal group has the special orthogonal group SO(n) as subgroup and the projective orthogonal group
Projective orthogonal group
In projective geometry and linear algebra, the projective orthogonal group PO is the induced action of the orthogonal group of a quadratic space V = A quadratic space is a vector space V together with a quadratic form Q; the Q is dropped from notation when it is clear. on the associated projective...
PO(n) as quotient, and the projective special orthogonal group PSO(n) as subquotient
Subquotient
In the mathematical fields of category theory and abstract algebra, a subquotient is a quotient object of a subobject. Subquotients are particularly important in group theory, where they are also known as sections, and in abelian categories....
, the unitary group has associated to it the special unitary group
Special unitary group
The special unitary group of degree n, denoted SU, is the group of n×n unitary matrices with determinant 1. The group operation is that of matrix multiplication...
SU(n), the projective unitary group
Projective unitary group
In mathematics, the projective unitary group PU is the quotient of the unitary group U by the right multiplication of its center, U, embedded as scalars....
PU(n), and the projective special unitary group PSU(n). These are related as by the commutative diagram at right; notably, both projective groups are equal:
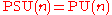 .
.The above is for the classical unitary group (over the complex numbers) – for unitary groups over finite fields, one similarly obtains special unitary and projective unitary groups, but in general
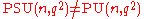 .
.G-structure: almost Hermitian
In the language of G-structureG-structure
In differential geometry, a G-structure on an n-manifold M, for a given structure group G, is a G-subbundle of the tangent frame bundle FM of M....
s, a manifold with a
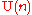 -structure is an almost Hermitian manifold.
-structure is an almost Hermitian manifold.Generalizations
From the point of view of Lie theoryLie theory
Lie theory is an area of mathematics, developed initially by Sophus Lie.Early expressions of Lie theory are found in books composed by Lie with Friedrich Engel and Georg Scheffers from 1888 to 1896....
, the classical unitary group is a real form of the Steinberg group
 , which is an algebraic group
, which is an algebraic groupAlgebraic group
In algebraic geometry, an algebraic group is a group that is an algebraic variety, such that the multiplication and inverse are given by regular functions on the variety...
that arises from the combination of the diagram automorphism of the general linear group (reversing the Dynkin diagram
 , which corresponds to transpose inverse) and the field automorphism of the extension
, which corresponds to transpose inverse) and the field automorphism of the extension 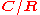 (namely complex conjugation). Both these automorphisms are automorphisms of the algebraic group, have order 2, and commute, and the unitary group is the fixed points of the product automorphism, as an algebraic group.
(namely complex conjugation). Both these automorphisms are automorphisms of the algebraic group, have order 2, and commute, and the unitary group is the fixed points of the product automorphism, as an algebraic group.The classical unitary group is a real form of this group, corresponding to the standard Hermitian form
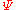 , which is positive definite.
, which is positive definite.This can be generalized in a number of ways:
- generalizing to other Hermitian forms yields indefinite unitary groups
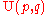 ;
; - the field extension can be replaced by any degree 2 separable algebra, most notably a degree 2 extension of a finite field;
- generalizing to other diagrams yields other groups of Lie type, namely the other Steinberg groups
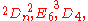 (in addition to
(in addition to  ) and Suzuki-Ree groups
) and Suzuki-Ree groups
-
-
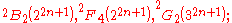
- considering a generalized unitary group as an algebraic group, one can take its points over various algebras.
-
Indefinite forms
Analogous to the indefinite orthogonal groups, one can define an indefinite unitary group, by considering the transforms that preserve a given Hermitian form, not necessarily positive definite (but generally taken to be non-degenerate). Here one is working with a vector space over the complex numbers.Given a Hermitian form
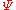 on a complex vector space
on a complex vector space  , the unitary group
, the unitary group 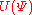 is the group of transforms that preserve the form: the transform
is the group of transforms that preserve the form: the transform  such that
such that 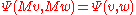 for all
for all  . In terms of matrices, representing the form by a matrix denoted
. In terms of matrices, representing the form by a matrix denoted  , this says that
, this says that 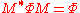 .
.Just as for symmetric forms over the reals, Hermitian forms are determined by signature, and are all unitarily congruent
Matrix congruence
In mathematics, two matrices A and B over a field are called congruent if there exists an invertible matrix P over the same field such thatwhere "T" denotes the matrix transpose...
to a diagonal form with
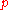 entries of 1 on the diagonal and
entries of 1 on the diagonal and 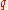 entries of
entries of 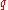 . The non-degenerate assumption is equivalent to
. The non-degenerate assumption is equivalent to 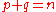 . In a standard basis, this is represented as a quadratic form as:
. In a standard basis, this is represented as a quadratic form as: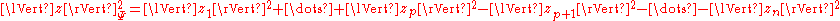
and as a symmetric form as:
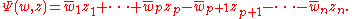
The resulting group is denoted
 .
.Finite fields
Over the finite fieldFinite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
with
 elements,
elements, 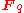 , there is a unique degree 2 extension field,
, there is a unique degree 2 extension field, 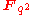 , with order 2 automorphism
, with order 2 automorphism 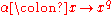 (the
(the  th power of the Frobenius automorphism). This allows one to define a Hermitian form on an
th power of the Frobenius automorphism). This allows one to define a Hermitian form on an 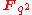 vector space
vector space  , as an
, as an 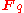 -bilinear map
-bilinear map 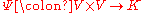 such that
such that 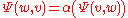 and
and  for
for  .
.Further, all non-degenerate Hermitian forms on a vector space over a finite field are unitarily congruent to the standard one, represented by the identity matrix, that is, any Hermitian form is unitarily equivalent to

where
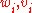 represent the coordinates of
represent the coordinates of 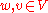 in some particular
in some particular 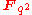 -basis of the
-basis of the  -dimensional space
-dimensional space  .
.Thus one can define a (unique) unitary group of dimension
 for the extension
for the extension 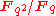 , denoted either as
, denoted either as 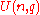 or
or 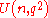 depending on the author. The subgroup of the unitary group consisting of matrices of determinant 1 is called the special unitary group and denoted
depending on the author. The subgroup of the unitary group consisting of matrices of determinant 1 is called the special unitary group and denoted 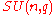 or
or  . For convenience, this article will use the
. For convenience, this article will use the 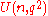 convention. The center of
convention. The center of 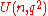 has order
has order  and consists of the scalar matrices which are unitary, that is those matrices
and consists of the scalar matrices which are unitary, that is those matrices 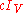 with
with  . The center of the special unitary group has order
. The center of the special unitary group has order 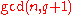 and consists of those unitary scalars which also have order dividing
and consists of those unitary scalars which also have order dividing  . The quotient of the unitary group by its center is called the projective unitary group
. The quotient of the unitary group by its center is called the projective unitary groupProjective unitary group
In mathematics, the projective unitary group PU is the quotient of the unitary group U by the right multiplication of its center, U, embedded as scalars....
,
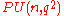 , and the quotient of the special unitary group by its center is the projective special unitary group
, and the quotient of the special unitary group by its center is the projective special unitary group 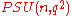 . In most cases (
. In most cases ( and
and  ),
),  is a perfect group
is a perfect groupPerfect group
In mathematics, more specifically in the area of modern algebra known as group theory, a group is said to be perfect if it equals its own commutator subgroup, or equivalently, if the group has no nontrivial abelian quotients...
and
 is a finite simple group
is a finite simple groupSimple group
In mathematics, a simple group is a nontrivial group whose only normal subgroups are the trivial group and the group itself. A group that is not simple can be broken into two smaller groups, a normal subgroup and the quotient group, and the process can be repeated...
, .
Degree-2 separable algebras
More generally, given a field k and a degree-2 separable k-algebra K (which may be a field extension but need not be),one can define unitary groups with respect to this extension.
First, there is a unique k-automorphism of K
 which is an involution and fixes exactly
which is an involution and fixes exactly 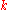 (
( if and only if
if and only if  ). This generalizes complex conjugation and the conjugation of degree 2 finite field extensions, and allows one to define Hermitian forms and unitary groups as above.
). This generalizes complex conjugation and the conjugation of degree 2 finite field extensions, and allows one to define Hermitian forms and unitary groups as above.Algebraic groups
The equations defining a unitary group are polynomial equations over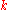 (but not over
(but not over  ): for the standard form
): for the standard form  the equations are given in matrices as
the equations are given in matrices as 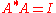 , where
, where  is the conjugate transpose
is the conjugate transposeConjugate transpose
In mathematics, the conjugate transpose, Hermitian transpose, Hermitian conjugate, or adjoint matrix of an m-by-n matrix A with complex entries is the n-by-m matrix A* obtained from A by taking the transpose and then taking the complex conjugate of each entry...
. Given a different form, they are
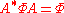 . The unitary group is thus an algebraic group
. The unitary group is thus an algebraic groupAlgebraic group
In algebraic geometry, an algebraic group is a group that is an algebraic variety, such that the multiplication and inverse are given by regular functions on the variety...
, whose points over a
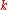 -algebra
-algebra  are given by:
are given by: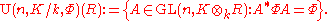
For the field extension
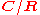 and the standard (positive definite) Hermitian form, these yield an algebraic group with real and complex points given by:
and the standard (positive definite) Hermitian form, these yield an algebraic group with real and complex points given by: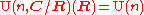
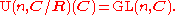
Polynomial invariants
The unitary groups are the automorphisms of two polynomials in real non-commutative variables:
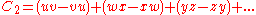
These are easily seen to be the real and imginary parts of the complex form
 . The two invariants separately are invariants of O(2n) and Sp(2n,R). Combined they make the invariants of U(n) which is a subgroup of both these groups. The variables must be non-commutative in these invariants otherwise the second polynomial is identically zero.
. The two invariants separately are invariants of O(2n) and Sp(2n,R). Combined they make the invariants of U(n) which is a subgroup of both these groups. The variables must be non-commutative in these invariants otherwise the second polynomial is identically zero.Classifying space
The classifying spaceClassifying space
In mathematics, specifically in homotopy theory, a classifying space BG of a topological group G is the quotient of a weakly contractible space EG by a free action of G...
for U(n) is described in the article classifying space for U(n)
Classifying space for U(n)
In mathematics, the classifying space for the unitary group U is a space B together with a universal bundle E such that any hermitian bundle on a paracompact space X is the pull-back of E by a map X → B unique up to homotopy.This space with its universal fibration may be constructed as either# the...
.

