P-group
Encyclopedia
In mathematics
, given a prime number
p, a p-group is a periodic group
in which each element has a power of p as its order
: each element is of prime power
order. That is, for each element g of the group, there exists a nonnegative integer n such that g to the power
pn is equal to the identity element
. Such groups are also called p-primary or simply primary.
A finite group
is a p-group if and only if its order
(the number of its elements) is a power of p. The remainder of this article deals with finite p-groups. For an example of an infinite abelian p-group, see Prüfer group
, and for an example of an infinite simple p-group, see Tarski monster group
.
This forms the basis for many inductive methods in p-groups.
For instance, the normalizer N of a proper subgroup H of a finite p-group G properly contains H, because for any counterexample
with H=N, the center Z is contained in N, and so also in H, but then there is a smaller example H/Z whose normalizer in G/Z is N/Z=H/Z, creating an infinite descent. As a corollary, every finite p-group is nilpotent
.
In another direction, every normal subgroup
of a finite p-group intersects the center nontrivially. In particular, every minimal normal subgroup of a finite p-group is of order p and contained in the center. Indeed, the socle
of a finite p-group is the subgroup of the center consisting of the central elements of order p.
If G is a p-group, then so is G/Z, and so it too has a nontrivial center. The preimage in G of the center of G/Z is called the second center and these groups begin the upper central series. Generalizing the earlier comments about the socle, a finite p-group with order pn contains normal subgroups of order pi with 0 ≤ i ≤ n, and any normal subgroup of order pi is contained in the ith center Zi. If a normal subgroup is not contained in Zi, then its intersection with Zi+1 has size at least pi+1.
. Every automorphism of G induces an automorphism on G/Φ(G), where Φ(G) is the Frattini subgroup
of G. The quotient G/Φ(G) is an elementary abelian group
and its automorphism group is a general linear group
, so very well understood. The map from the automorphism group of G into this general linear group has been studied by Burnside
, who showed that the kernel of this map is a p-group.
; for example, the cyclic group
C4 and the Klein group V4 are both 2-groups of order 4, but they are not isomorphic.
Nor need a p-group be abelian
; the dihedral group
Dih4 of order 8 is a non-abelian 2-group. However, every group of order p2 is abelian.To prove that a group of order p2 is abelian, note that it is a p-group so has non-trivial center, so given a non-trivial element of the center g, this either generates the group (so G is cyclic, hence abelian: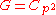
), or it generates a subgroup of order p, so g and some element h not in its orbit generate G, (since the subgroup they generate must have order 
) but they commute since g is central, so the group is abelian, and in fact 
The dihedral groups are both very similar to and very dissimilar from the quaternion group
s and the semidihedral groups. Together the dihedral, semidihedral, and quaternion groups form the 2-groups of maximal class, that is those groups of order 2n+1 and nilpotency class n.
s of cyclic groups of order p are very important examples of p-groups. Denote the cyclic group of order p as W(1), and the wreath product of W(n) with W(1) as W(n+1). Then W(n) is the Sylow p-subgroup of the symmetric group
Sym(pn). Maximal p-subgroups of the general linear group GL(n,Q) are direct products of various W(n). It has order pk where k=(pn−1)/(p−1). It has nilpotency class pn−1, and its lower central series, upper central series, lower exponent-p central series, and upper exponent-p central series are equal. It is generated by its elements of order p, but its exponent is pn. The second such group, W(2), is also a p-group of maximal class, since it has order pp+1 and nilpotency class p, but is not a regular p-group
. Since groups of order pp are always regular groups, it is also a minimal such example.
generated by 1−ζ. Let G be a cyclic group of order p generated by an element z. Form the semidirect product
E(p) of Z[ζ] and G where z acts as multiplication by ζ. The powers Pn are normal subgroups of E(p), and the example groups are E(p,n) = E(p)/Pn. E(p,n) has order pn+1 and nilpotency class n, so is a p-group of maximal class. When p=2, E(2,n) is the dihedral group of order 2n. When p is odd, both W(2) and E(p,p) are irregular groups of maximal class and order pp+1, but are not isomorphic.
s are another fundamental family of examples. Let V be a vector space of dimension n with basis { e1, e2, …, en } and define Vi to be the vector space generated by { ei, ei+1, …, en } for 1 ≤ i ≤ n, and define Vi = 0 when i > n. For each 1 ≤ m ≤ n, the set of invertible linear transformations of V which take each Vi to Vi+m form a subgroup of Aut(V) denoted Um. If V is a vector space over Z/pZ, then U1 is a Sylow p-subgroup of Aut(V) = GL(n, p), and the terms of its lower central series are just the Um. In terms of matrices, Um are those upper triangular matrices with 1s one the diagonal and 0s on the first m−1 superdiagonals. The group U1 has order pn·(n−1)/2, nilpotency class n, and exponent pk where k is the least integer at least as large as the base p logarithm
of n.
.
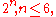Rather than classify the groups by order, Philip Hall
proposed using a notion of isoclinism of groups
which gathered finite p-groups into families based on large quotient and subgroups .
An entirely different method classifies finite p-groups by their coclass, that is, the difference between their composition length
and their nilpotency class
. The so-called coclass conjectures described the set of all finite p-groups of fixed coclass as perturbations of finitely many pro-p group
s. The coclass conjectures were proven in the 1980s using techniques related to Lie algebra
s and powerful p-group
s .
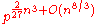, and these are dominated by the classes that are two-step nilpotent . Because of this rapid growth, there is a folklore conjecture asserting that almost all finite group
s are 2-groups: the fraction of isomorphism class
es of 2-groups among isomorphism classes of groups of order at most n is thought to tend to 1 as n tends to infinity. For instance, of the 49 910 529 484 different groups of order at most 2000, 49 487 365 422, or just over 99%, are 2-groups of order 1024 .
. In fact, it contains a p-group of maximal possible order: if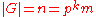
where p does not divide m, then G has a subgroup P of order 
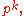called a Sylow p-subgroup. This subgroup need not be unique, but any subgroups of this order are conjugate, and any p-subgroup of G is contained in a Sylow p-subgroup. This and other properties are proved in the Sylow theorems.
. p-groups arise both as subgroups and as quotient groups. As subgroups, for a given prime p one has the Sylow p-subgroups P (largest p-subgroup not unique but all conjugate) and the p-core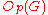
(the unique largest normal p-subgroup), and various others. As quotients, the largest p-group quotient is the quotient of G by the p-residual subgroup 
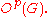These groups are related (for different primes), possess important properties such as the focal subgroup theorem
, and allow one to determine many aspects of the structure of the group.
The large elementary abelian subgroup
s of a finite group exert control over the group that was used in the proof of the Feit–Thompson theorem
. Certain central extensions of elementary abelian groups called extraspecial groups help describe the structure of groups as acting symplectic vector space
s.
Brauer
classified all groups whose Sylow 2-subgroups are the direct product of two cyclic groups of order 4, and Walter, Gorenstein
, Bender, Suzuki
, Glauberman
, and others classified those simple groups whose Sylow 2-subgroups were abelian, dihedral, semidihedral, or quaternion.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, given a prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
p, a p-group is a periodic group
Periodic group
In group theory, a periodic group or a torsion group is a group in which each element has finite order. All finite groups are periodic. The concept of a periodic group should not be confused with that of a cyclic group, although all finite cyclic groups are periodic.The exponent of a periodic group...
in which each element has a power of p as its order
Order (group theory)
In group theory, a branch of mathematics, the term order is used in two closely related senses:* The order of a group is its cardinality, i.e., the number of its elements....
: each element is of prime power
Prime power
In mathematics, a prime power is a positive integer power of a prime number.For example: 5=51, 9=32 and 16=24 are prime powers, while6=2×3, 15=3×5 and 36=62=22×32 are not...
order. That is, for each element g of the group, there exists a nonnegative integer n such that g to the power
Exponentiation
Exponentiation is a mathematical operation, written as an, involving two numbers, the base a and the exponent n...
pn is equal to the identity element
Identity element
In mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
. Such groups are also called p-primary or simply primary.
A finite group
Finite group
In mathematics and abstract algebra, a finite group is a group whose underlying set G has finitely many elements. During the twentieth century, mathematicians investigated certain aspects of the theory of finite groups in great depth, especially the local theory of finite groups, and the theory of...
is a p-group if and only if its order
Order (group theory)
In group theory, a branch of mathematics, the term order is used in two closely related senses:* The order of a group is its cardinality, i.e., the number of its elements....
(the number of its elements) is a power of p. The remainder of this article deals with finite p-groups. For an example of an infinite abelian p-group, see Prüfer group
Prüfer group
In mathematics, specifically in group theory, the Prüfer p-group or the p-quasicyclic group or p∞-group, Z, for a prime number p is the unique p-group in which every element has p pth roots. The group is named after Heinz Prüfer...
, and for an example of an infinite simple p-group, see Tarski monster group
Tarski monster group
In mathematics, a Tarski monster group, named for Alfred Tarski, is an infinite group G, such that every proper subgroup H of G, other than the identity subgroup, is a cyclic group of order a fixed prime number p. A Tarski monster group is necessarily simple. It was shown by A. Yu...
.
Non-trivial center
One of the first standard results using the class equation is that the center of a non-trivial finite p-group cannot be the trivial subgroup (proof).This forms the basis for many inductive methods in p-groups.
For instance, the normalizer N of a proper subgroup H of a finite p-group G properly contains H, because for any counterexample
Counterexample
In logic, and especially in its applications to mathematics and philosophy, a counterexample is an exception to a proposed general rule. For example, consider the proposition "all students are lazy"....
with H=N, the center Z is contained in N, and so also in H, but then there is a smaller example H/Z whose normalizer in G/Z is N/Z=H/Z, creating an infinite descent. As a corollary, every finite p-group is nilpotent
Nilpotent group
In mathematics, more specifically in the field of group theory, a nilpotent group is a group that is "almost abelian". This idea is motivated by the fact that nilpotent groups are solvable, and for finite nilpotent groups, two elements having relatively prime orders must commute...
.
In another direction, every normal subgroup
Normal subgroup
In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
of a finite p-group intersects the center nontrivially. In particular, every minimal normal subgroup of a finite p-group is of order p and contained in the center. Indeed, the socle
Socle (mathematics)
-Socle of a group:In the context of group theory, the socle of a group G, denoted Soc, is the subgroup generated by the minimal non-trivial normal subgroups of G. The socle is a direct product of minimal normal subgroups...
of a finite p-group is the subgroup of the center consisting of the central elements of order p.
If G is a p-group, then so is G/Z, and so it too has a nontrivial center. The preimage in G of the center of G/Z is called the second center and these groups begin the upper central series. Generalizing the earlier comments about the socle, a finite p-group with order pn contains normal subgroups of order pi with 0 ≤ i ≤ n, and any normal subgroup of order pi is contained in the ith center Zi. If a normal subgroup is not contained in Zi, then its intersection with Zi+1 has size at least pi+1.
Automorphisms
The automorphism groups of p-groups are well studied. Just as every finite p-group has a nontrivial center so that the inner automorphism group is a proper quotient of the group, every finite p-group has a nontrivial outer automorphism groupOuter automorphism group
In mathematics, the outer automorphism group of a group Gis the quotient Aut / Inn, where Aut is the automorphism group of G and Inn is the subgroup consisting of inner automorphisms. The outer automorphism group is usually denoted Out...
. Every automorphism of G induces an automorphism on G/Φ(G), where Φ(G) is the Frattini subgroup
Frattini subgroup
In mathematics, the Frattini subgroup Φ of a group G is the intersection of all maximal subgroups of G. For the case that G is the trivial group e, which has no maximal subgroups, it is defined by Φ = e...
of G. The quotient G/Φ(G) is an elementary abelian group
Elementary Abelian group
In group theory, an elementary abelian group is a finite abelian group, where every nontrivial element has order p, where p is a prime; in particular it is a p-group....
and its automorphism group is a general linear group
General linear group
In mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible...
, so very well understood. The map from the automorphism group of G into this general linear group has been studied by Burnside
William Burnside
William Burnside was an English mathematician. He is known mostly as an early contributor to the theory of finite groups....
, who showed that the kernel of this map is a p-group.
Examples
p-groups of the same order are not necessarily isomorphicIsomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
; for example, the cyclic group
Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
C4 and the Klein group V4 are both 2-groups of order 4, but they are not isomorphic.
Nor need a p-group be abelian
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
; the dihedral group
Dihedral group
In mathematics, a dihedral group is the group of symmetries of a regular polygon, including both rotations and reflections. Dihedral groups are among the simplest examples of finite groups, and they play an important role in group theory, geometry, and chemistry.See also: Dihedral symmetry in three...
Dih4 of order 8 is a non-abelian 2-group. However, every group of order p2 is abelian.To prove that a group of order p2 is abelian, note that it is a p-group so has non-trivial center, so given a non-trivial element of the center g, this either generates the group (so G is cyclic, hence abelian:
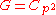), or it generates a subgroup of order p, so g and some element h not in its orbit generate G, (since the subgroup they generate must have order ) but they commute since g is central, so the group is abelian, and in fact The dihedral groups are both very similar to and very dissimilar from the quaternion group
Quaternion group
In group theory, the quaternion group is a non-abelian group of order eight, isomorphic to a certain eight-element subset of the quaternions under multiplication...
s and the semidihedral groups. Together the dihedral, semidihedral, and quaternion groups form the 2-groups of maximal class, that is those groups of order 2n+1 and nilpotency class n.
Iterated wreath products
The iterated wreath productWreath product
In mathematics, the wreath product of group theory is a specialized product of two groups, based on a semidirect product. Wreath products are an important tool in the classification of permutation groups and also provide a way of constructing interesting examples of groups.Given two groups A and H...
s of cyclic groups of order p are very important examples of p-groups. Denote the cyclic group of order p as W(1), and the wreath product of W(n) with W(1) as W(n+1). Then W(n) is the Sylow p-subgroup of the symmetric group
Symmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
Sym(pn). Maximal p-subgroups of the general linear group GL(n,Q) are direct products of various W(n). It has order pk where k=(pn−1)/(p−1). It has nilpotency class pn−1, and its lower central series, upper central series, lower exponent-p central series, and upper exponent-p central series are equal. It is generated by its elements of order p, but its exponent is pn. The second such group, W(2), is also a p-group of maximal class, since it has order pp+1 and nilpotency class p, but is not a regular p-group
Regular p-group
In mathematical finite group theory, the concept of regular p-group captures some of the more important properties of abelian p-groups, but is general enough to include most "small" p-groups...
. Since groups of order pp are always regular groups, it is also a minimal such example.
Generalized dihedral groups
When p=2 and n=2, W(n) is the dihedral group of order 8, so in some sense W(n) provides an analogue for the dihedral group for all primes p when n=2. However, for higher n the analogy becomes strained. There is a different family of examples that more closely mimics the dihedral groups of order 2n, but that requires a bit more setup. Let ζ denote a primitive pth root of unity in the complex numbers, and let Z[ζ] be the ring of cyclotomic integers generated by it, and let P be the prime idealPrime ideal
In algebra , a prime ideal is a subset of a ring which shares many important properties of a prime number in the ring of integers...
generated by 1−ζ. Let G be a cyclic group of order p generated by an element z. Form the semidirect product
Semidirect product
In mathematics, specifically in the area of abstract algebra known as group theory, a semidirect product is a particular way in which a group can be put together from two subgroups, one of which is a normal subgroup. A semidirect product is a generalization of a direct product...
E(p) of Z[ζ] and G where z acts as multiplication by ζ. The powers Pn are normal subgroups of E(p), and the example groups are E(p,n) = E(p)/Pn. E(p,n) has order pn+1 and nilpotency class n, so is a p-group of maximal class. When p=2, E(2,n) is the dihedral group of order 2n. When p is odd, both W(2) and E(p,p) are irregular groups of maximal class and order pp+1, but are not isomorphic.
Unitriangular matrix groups
The Sylow subgroups of general linear groupGeneral linear group
In mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible...
s are another fundamental family of examples. Let V be a vector space of dimension n with basis { e1, e2, …, en } and define Vi to be the vector space generated by { ei, ei+1, …, en } for 1 ≤ i ≤ n, and define Vi = 0 when i > n. For each 1 ≤ m ≤ n, the set of invertible linear transformations of V which take each Vi to Vi+m form a subgroup of Aut(V) denoted Um. If V is a vector space over Z/pZ, then U1 is a Sylow p-subgroup of Aut(V) = GL(n, p), and the terms of its lower central series are just the Um. In terms of matrices, Um are those upper triangular matrices with 1s one the diagonal and 0s on the first m−1 superdiagonals. The group U1 has order pn·(n−1)/2, nilpotency class n, and exponent pk where k is the least integer at least as large as the base p logarithm
Logarithm
The logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
of n.
Classification
The groups of order pn for 0 ≤ n ≤ 4 were classified early in the history of group theory , and modern work has extended these classifications to groups whose order divides p7, though the sheer number of families of such groups grows so quickly that further classifications along these lines are judged difficult for the human mind to comprehend . An example is , which classifies groups of order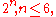.Rather than classify the groups by order, Philip Hall
Philip Hall
Philip Hall FRS , was an English mathematician.His major work was on group theory, notably on finite groups and solvable groups.-Biography:...
proposed using a notion of isoclinism of groups
Isoclinism of groups
In mathematics, specifically group theory, isoclinism is an equivalence relation on groups that is broader than isomorphism, that is, any two groups that are isomorphic are isoclinic, but two isoclinic groups may not be isomorphic. The concept of isoclinism was introduced by to help classify and...
which gathered finite p-groups into families based on large quotient and subgroups .
An entirely different method classifies finite p-groups by their coclass, that is, the difference between their composition length
Composition series
In abstract algebra, a composition series provides a way to break up an algebraic structure, such as a group or a module, into simple pieces. The need for considering composition series in the context of modules arises from the fact that many naturally occurring modules are not semisimple, hence...
and their nilpotency class
Nilpotent group
In mathematics, more specifically in the field of group theory, a nilpotent group is a group that is "almost abelian". This idea is motivated by the fact that nilpotent groups are solvable, and for finite nilpotent groups, two elements having relatively prime orders must commute...
. The so-called coclass conjectures described the set of all finite p-groups of fixed coclass as perturbations of finitely many pro-p group
Pro-p group
In mathematics, a pro-p group is a profinite group G such that for any open normal subgroup N\triangleleft G the quotient group G/N is a p-group...
s. The coclass conjectures were proven in the 1980s using techniques related to Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
s and powerful p-group
Powerful p-group
In mathematics, in the field of group theory, especially in the study of p-groups and pro-p-groups, the concept of powerful p-groups plays an important role. They were introduced in , where a number of applications are given, including results on Schur multipliers...
s .
Among groups
The number of isomorphism classes of groups of order pn grows as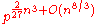, and these are dominated by the classes that are two-step nilpotent . Because of this rapid growth, there is a folklore conjecture asserting that almost all finite groupFinite group
In mathematics and abstract algebra, a finite group is a group whose underlying set G has finitely many elements. During the twentieth century, mathematicians investigated certain aspects of the theory of finite groups in great depth, especially the local theory of finite groups, and the theory of...
s are 2-groups: the fraction of isomorphism class
Isomorphism class
An isomorphism class is a collection of mathematical objects isomorphic to each other.Isomorphism classes are often defined if the exact identity of the elements of the set is considered irrelevant, and the properties of the structure of the mathematical object are studied. Examples of this are...
es of 2-groups among isomorphism classes of groups of order at most n is thought to tend to 1 as n tends to infinity. For instance, of the 49 910 529 484 different groups of order at most 2000, 49 487 365 422, or just over 99%, are 2-groups of order 1024 .
Within a group
Every finite group whose order is divisible by p contains a subgroup which is a non-trivial p-group, namely a cyclic group of order p generated by an element of order p obtained from Cauchy's theoremCauchy's theorem (group theory)
Cauchy's theorem is a theorem in the mathematics of group theory, named after Augustin Louis Cauchy. It states that if G is a finite group and p is a prime number dividing the order of G , then G contains an element of order p...
. In fact, it contains a p-group of maximal possible order: if
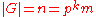where p does not divide m, then G has a subgroup P of order 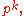called a Sylow p-subgroup. This subgroup need not be unique, but any subgroups of this order are conjugate, and any p-subgroup of G is contained in a Sylow p-subgroup. This and other properties are proved in the Sylow theorems.Application to structure of a group
p-groups are fundamental tools in understanding the structure of groups and in the classification of finite simple groupsClassification of finite simple groups
In mathematics, the classification of the finite simple groups is a theorem stating that every finite simple group belongs to one of four categories described below. These groups can be seen as the basic building blocks of all finite groups, in much the same way as the prime numbers are the basic...
. p-groups arise both as subgroups and as quotient groups. As subgroups, for a given prime p one has the Sylow p-subgroups P (largest p-subgroup not unique but all conjugate) and the p-core
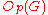(the unique largest normal p-subgroup), and various others. As quotients, the largest p-group quotient is the quotient of G by the p-residual subgroup 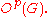These groups are related (for different primes), possess important properties such as the focal subgroup theoremFocal subgroup theorem
In abstract algebra, the focal subgroup theorem describes the fusion of elements in a Sylow subgroup of a finite group. The focal subgroup theorem was introduced in and is the "first major application of the transfer" according to . The focal subgroup theorem relates the ideas of transfer and...
, and allow one to determine many aspects of the structure of the group.
Local control
Much of the structure of a finite group is carried in the structure of its so-called local subgroups, the normalizers of non-identity p-subgroups .The large elementary abelian subgroup
Elementary Abelian group
In group theory, an elementary abelian group is a finite abelian group, where every nontrivial element has order p, where p is a prime; in particular it is a p-group....
s of a finite group exert control over the group that was used in the proof of the Feit–Thompson theorem
Feit–Thompson theorem
In mathematics, the Feit–Thompson theorem, or odd order theorem, states that every finite group of odd order is solvable. It was proved by - History : conjectured that every nonabelian finite simple group has even order...
. Certain central extensions of elementary abelian groups called extraspecial groups help describe the structure of groups as acting symplectic vector space
Symplectic vector space
In mathematics, a symplectic vector space is a vector space V equipped with a bilinear form ω : V × V → R that is...
s.
Brauer
Richard Brauer
Richard Dagobert Brauer was a leading German and American mathematician. He worked mainly in abstract algebra, but made important contributions to number theory...
classified all groups whose Sylow 2-subgroups are the direct product of two cyclic groups of order 4, and Walter, Gorenstein
Daniel Gorenstein
Daniel E. Gorenstein was an American mathematician. He earned his undergraduate and graduate degrees at Harvard University, where he earned his Ph.D. in 1950 under Oscar Zariski, introducing in his dissertation Gorenstein rings...
, Bender, Suzuki
Michio Suzuki
was a Japanese mathematician who studied group theory.-Biography:He was a Professor at the University of Illinois at Urbana-Champaign from 1953 to his death. He also had visiting positions at the University of Chicago , the Institute for Advanced Study , the University of Tokyo , and the...
, Glauberman
George Glauberman
George Glauberman is a mathematician at the University of Chicago who works on finite simple groups. He proved the ZJ theorem and the Z* theorem....
, and others classified those simple groups whose Sylow 2-subgroups were abelian, dihedral, semidihedral, or quaternion.