
List of mathematical functions
Encyclopedia
In mathematics
, several function
s or groups of functions are important enough to deserve their own names. This is a listing of pointers to those articles which explain these functions in more detail. There is a large theory of special functions
which developed out of statistics
and mathematical physics
. A modern, abstract point of view contrasts large function space
s, which are infinite-dimensional and within which most functions are 'anonymous', with special functions picked out by properties such as symmetry
, or relationship to harmonic analysis
and group representation
s.
See also List of types of functions
s are functions that can be expressed as the solution of a polynomial equation with integer coefficients.
s are functions that are not algebraic.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, several function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
s or groups of functions are important enough to deserve their own names. This is a listing of pointers to those articles which explain these functions in more detail. There is a large theory of special functions
Special functions
Special functions are particular mathematical functions which have more or less established names and notations due to their importance in mathematical analysis, functional analysis, physics, or other applications....
which developed out of statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
and mathematical physics
Mathematical physics
Mathematical physics refers to development of mathematical methods for application to problems in physics. The Journal of Mathematical Physics defines this area as: "the application of mathematics to problems in physics and the development of mathematical methods suitable for such applications and...
. A modern, abstract point of view contrasts large function space
Function space
In mathematics, a function space is a set of functions of a given kind from a set X to a set Y. It is called a space because in many applications it is a topological space, a vector space, or both.-Examples:...
s, which are infinite-dimensional and within which most functions are 'anonymous', with special functions picked out by properties such as symmetry
Symmetry
Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...
, or relationship to harmonic analysis
Harmonic analysis
Harmonic analysis is the branch of mathematics that studies the representation of functions or signals as the superposition of basic waves. It investigates and generalizes the notions of Fourier series and Fourier transforms...
and group representation
Group representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
s.
See also List of types of functions
Elementary functions
Elementary functions are functions built from basic operations (e.g. addition, exponentials, logarithms...)Algebraic functions
Algebraic functionAlgebraic function
In mathematics, an algebraic function is informally a function that satisfies a polynomial equation whose coefficients are themselves polynomials with rational coefficients. For example, an algebraic function in one variable x is a solution y for an equationwhere the coefficients ai are polynomial...
s are functions that can be expressed as the solution of a polynomial equation with integer coefficients.
- PolynomialPolynomialIn mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
s: Can be generated by addition and multiplication alone.- Linear functionLinear functionIn mathematics, the term linear function can refer to either of two different but related concepts:* a first-degree polynomial function of one variable;* a map between two vector spaces that preserves vector addition and scalar multiplication....
: First degree polynomial, graph is a straight line. - Quadratic functionQuadratic functionA quadratic function, in mathematics, is a polynomial function of the formf=ax^2+bx+c,\quad a \ne 0.The graph of a quadratic function is a parabola whose axis of symmetry is parallel to the y-axis....
: Second degree polynomial, graph is a parabolaParabolaIn mathematics, the parabola is a conic section, the intersection of a right circular conical surface and a plane parallel to a generating straight line of that surface...
. - Cubic functionCubic functionIn mathematics, a cubic function is a function of the formf=ax^3+bx^2+cx+d,\,where a is nonzero; or in other words, a polynomial of degree three. The derivative of a cubic function is a quadratic function...
: Third degree polynomial. - Quartic functionQuartic functionIn mathematics, a quartic function, or equation of the fourth degree, is a function of the formf=ax^4+bx^3+cx^2+dx+e \,where a is nonzero; or in other words, a polynomial of degree four...
: Fourth degree polynomial. - Quintic functionQuintic equationIn mathematics, a quintic function is a function of the formg=ax^5+bx^4+cx^3+dx^2+ex+f,\,where a, b, c, d, e and f are members of a field, typically the rational numbers, the real numbers or the complex numbers, and a is nonzero...
: Fifth degree polynomial. - Sextic functionSextic equationIn mathematics, a sextic equation is a polynomial equation of degree six. It is of the form:ax^6+bx^5+cx^4+dx^3+ex^2+fx+g=0,\,where a \neq 0....
: Sixth degree polynomial.
- Linear function
- Rational functionRational functionIn mathematics, a rational function is any function which can be written as the ratio of two polynomial functions. Neither the coefficients of the polynomials nor the values taken by the function are necessarily rational.-Definitions:...
s: A ratio of two polynomials. - Nth rootNth rootIn mathematics, the nth root of a number x is a number r which, when raised to the power of n, equals xr^n = x,where n is the degree of the root...
- Square rootSquare rootIn mathematics, a square root of a number x is a number r such that r2 = x, or, in other words, a number r whose square is x...
: Yields a number whose square is the given one .
. - Cube root: Yields a number whose cube is the given one
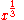 .
.
- Square root
Elementary transcendental functions
Transcendental functionTranscendental function
A transcendental function is a function that does not satisfy a polynomial equation whose coefficients are themselves polynomials, in contrast to an algebraic function, which does satisfy such an equation...
s are functions that are not algebraic.
- Exponential functionExponential functionIn mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
: raises a fixed number to a variable power. - Hyperbolic functionHyperbolic functionIn mathematics, hyperbolic functions are analogs of the ordinary trigonometric, or circular, functions. The basic hyperbolic functions are the hyperbolic sine "sinh" , and the hyperbolic cosine "cosh" , from which are derived the hyperbolic tangent "tanh" and so on.Just as the points form a...
s: formally similar to the trigonometric functions. - LogarithmLogarithmThe logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
s: the inverses of exponential functions; useful to solve equations involving exponentials.- Natural logarithmNatural logarithmThe natural logarithm is the logarithm to the base e, where e is an irrational and transcendental constant approximately equal to 2.718281828...
- Common logarithmCommon logarithmThe common logarithm is the logarithm with base 10. It is also known as the decadic logarithm, named after its base. It is indicated by log10, or sometimes Log with a capital L...
- Binary logarithmBinary logarithmIn mathematics, the binary logarithm is the logarithm to the base 2. It is the inverse function of n ↦ 2n. The binary logarithm of n is the power to which the number 2 must be raised to obtain the value n. This makes the binary logarithm useful for anything involving powers of 2,...
- Indefinite logarithmIndefinite logarithmThe indefinite logarithm of a positive number n is the logarithm without regard to any particular base: it is a function , not a number...
- Natural logarithm
- Power functionsExponentiationExponentiation is a mathematical operation, written as an, involving two numbers, the base a and the exponent n...
: raise a variable number to a fixed power; also known as Allometric functions; note: if the power is a rational number it is not strictly a transcendental function. - Periodic functionPeriodic functionIn mathematics, a periodic function is a function that repeats its values in regular intervals or periods. The most important examples are the trigonometric functions, which repeat over intervals of length 2π radians. Periodic functions are used throughout science to describe oscillations,...
s- Trigonometric functionTrigonometric functionIn mathematics, the trigonometric functions are functions of an angle. They are used to relate the angles of a triangle to the lengths of the sides of a triangle...
s: sine, cosine, tangent, etc.; used in geometryGeometryGeometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
and to describe periodic phenomena. See also Gudermannian function. - Sawtooth waveSawtooth waveThe sawtooth wave is a kind of non-sinusoidal waveform. It is named a sawtooth based on its resemblance to the teeth on the blade of a saw....
- Square waveSquare waveA square wave is a kind of non-sinusoidal waveform, most typically encountered in electronics and signal processing. An ideal square wave alternates regularly and instantaneously between two levels...
- Triangle waveTriangle waveA triangle wave is a non-sinusoidal waveform named for its triangular shape.Like a square wave, the triangle wave contains only odd harmonics...
- Trigonometric function
Basic special functions
- Indicator function: maps x to either 1 or 0, depending on whether or not x belongs to some subset.
- Step functionStep functionIn mathematics, a function on the real numbers is called a step function if it can be written as a finite linear combination of indicator functions of intervals...
: A finite linear combinationLinear combinationIn mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...
of indicator functions of half-open intervals.- Floor functionFloor functionIn mathematics and computer science, the floor and ceiling functions map a real number to the largest previous or the smallest following integer, respectively...
: Largest integer less than or equal to a given number. - Heaviside step functionHeaviside step functionThe Heaviside step function, or the unit step function, usually denoted by H , is a discontinuous function whose value is zero for negative argument and one for positive argument....
: 0 for negative arguments and 1 for positive arguments. The integral of the Dirac delta functionDirac delta functionThe Dirac delta function, or δ function, is a generalized function depending on a real parameter such that it is zero for all values of the parameter except when the parameter is zero, and its integral over the parameter from −∞ to ∞ is equal to one. It was introduced by theoretical...
. - Sign functionSign functionIn mathematics, the sign function is an odd mathematical function that extracts the sign of a real number. To avoid confusion with the sine function, this function is often called the signum function ....
: Returns only the sign of a number, as +1 or −1.
- Floor function
- Absolute valueAbsolute valueIn mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
: distance to the origin (zero point)
Number theoretic functions
- Sigma functionDivisor functionIn mathematics, and specifically in number theory, a divisor function is an arithmetical function related to the divisors of an integer. When referred to as the divisor function, it counts the number of divisors of an integer. It appears in a number of remarkable identities, including relationships...
: SumSUMSUM can refer to:* The State University of Management* Soccer United Marketing* Society for the Establishment of Useful Manufactures* StartUp-Manager* Software User’s Manual,as from DOD-STD-2 167A, and MIL-STD-498...
s of powerExponentiationExponentiation is a mathematical operation, written as an, involving two numbers, the base a and the exponent n...
s of divisorDivisorIn mathematics, a divisor of an integer n, also called a factor of n, is an integer which divides n without leaving a remainder.-Explanation:...
s of a given natural numberNatural numberIn mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
. - Euler's totient functionEuler's totient functionIn number theory, the totient \varphi of a positive integer n is defined to be the number of positive integers less than or equal to n that are coprime to n In number theory, the totient \varphi(n) of a positive integer n is defined to be the number of positive integers less than or equal to n that...
: Number of numbers coprimeCoprimeIn number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...
to (and not bigger than) a given one. - Prime-counting function: Number of primePrime numberA prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
s less than or equal to a given number. - Partition function: Order-independent count of ways to write a given positive integer as a sum of positive integers.
Antiderivatives of elementary functions
- Logarithmic integral functionLogarithmic integral functionIn mathematics, the logarithmic integral function or integral logarithm li is a special function. It occurs in problems of physics and has number theoretic significance, occurring in the prime number theorem as an estimate of the number of prime numbers less than a given value.-Integral...
: Integral of the reciprocal of the logarithm, important in the prime number theoremPrime number theoremIn number theory, the prime number theorem describes the asymptotic distribution of the prime numbers. The prime number theorem gives a general description of how the primes are distributed amongst the positive integers....
. - Exponential integralExponential integralIn mathematics, the exponential integral is a special function defined on the complex plane given the symbol Ei.-Definitions:For real, nonzero values of x, the exponential integral Ei can be defined as...
- Trigonometric integralTrigonometric integralIn mathematics, the trigonometric integrals are a family of integrals which involve trigonometric functions. A number of the basic trigonometric integrals are discussed at the list of integrals of trigonometric functions.-Sine integral:...
: Including Sine Integral and Cosine Integral - Error functionError functionIn mathematics, the error function is a special function of sigmoid shape which occurs in probability, statistics and partial differential equations...
: An integral important for normal random variables.- Fresnel integralFresnel integral250px|thumb|S and C The maximum of C is about 0.977451424. If πt²/2 were used instead of t², then the image would be scaled vertically and horizontally ....
: related to the error function; used in opticsOpticsOptics is the branch of physics which involves the behavior and properties of light, including its interactions with matter and the construction of instruments that use or detect it. Optics usually describes the behavior of visible, ultraviolet, and infrared light...
. - Dawson function: occurs in probabilityProbabilityProbability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
.
- Fresnel integral
Gamma and related functions
- Gamma functionGamma functionIn mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...
: A generalization of the factorialFactorialIn mathematics, the factorial of a non-negative integer n, denoted by n!, is the product of all positive integers less than or equal to n...
function. - Barnes G-functionBarnes G-functionIn mathematics, the Barnes G-function G is a function that is an extension of superfactorials to the complex numbers. It is related to the Gamma function, the K-function and the Glaisher-Kinkelin constant, and was named after mathematician Ernest William Barnes...
- Beta function: Corresponding binomial coefficientBinomial coefficientIn mathematics, binomial coefficients are a family of positive integers that occur as coefficients in the binomial theorem. They are indexed by two nonnegative integers; the binomial coefficient indexed by n and k is usually written \tbinom nk , and it is the coefficient of the x k term in...
analogue. - Digamma function, Polygamma function
- Incomplete beta function
- Incomplete gamma functionIncomplete gamma functionIn mathematics, the gamma function is defined by a definite integral. The incomplete gamma function is defined as an integral function of the same integrand. There are two varieties of the incomplete gamma function: the upper incomplete gamma function is for the case that the lower limit of...
- K-functionK-functionIn mathematics, the K-function, typically denoted K, is a generalization of the hyperfactorial to complex numbers, similar to the generalization of the factorial to the Gamma function.Formally, the K-function is defined as...
- Multivariate gamma functionMultivariate gamma functionIn mathematics, the multivariate Gamma function, Γp, is a generalization of the Gamma function. It is useful in multivariate statistics, appearing in the probability density function of the Wishart and Inverse Wishart distributions....
: A generalization of the Gamma function useful in multivariate statisticsMultivariate statisticsMultivariate statistics is a form of statistics encompassing the simultaneous observation and analysis of more than one statistical variable. The application of multivariate statistics is multivariate analysis...
. - Student's t-distribution
Elliptic and related functions
- Elliptic integralElliptic integralIn integral calculus, elliptic integrals originally arose in connection with the problem of giving the arc length of an ellipse. They were first studied by Giulio Fagnano and Leonhard Euler...
s: Arising from the path length of ellipseEllipseIn geometry, an ellipse is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve. Circles are special cases of ellipses, obtained when the cutting plane is orthogonal to the cone's axis...
s; important in many applications. Related functions are the quarter period and the nome. Alternate notations include:- Carlson symmetric formCarlson symmetric formIn mathematics, the Carlson symmetric forms of elliptic integrals are a small canonical set of elliptic integrals to which all others may be reduced. They are a modern alternative to the Legendre forms...
- Legendre form
- Carlson symmetric form
- Elliptic functionElliptic functionIn complex analysis, an elliptic function is a function defined on the complex plane that is periodic in two directions and at the same time is meromorphic...
s: The inverses of elliptic integrals; used to model double-periodic phenomena. Particular types are Weierstrass's elliptic functionsWeierstrass's elliptic functionsIn mathematics, Weierstrass's elliptic functions are elliptic functions that take a particularly simple form; they are named for Karl Weierstrass...
and Jacobi's elliptic functionsJacobi's elliptic functionsIn mathematics, the Jacobi elliptic functions are a set of basic elliptic functions, and auxiliary theta functions, that have historical importance with also many features that show up important structure, and have direct relevance to some applications...
. - Theta function
- Closely related are the modular formModular formIn mathematics, a modular form is a analytic function on the upper half-plane satisfying a certain kind of functional equation and growth condition. The theory of modular forms therefore belongs to complex analysis but the main importance of the theory has traditionally been in its connections...
s, which include- J-invariantJ-invariantIn mathematics, Klein's j-invariant, regarded as a function of a complex variable τ, is a modular function defined on the upper half-plane of complex numbers.We haveThe modular discriminant \Delta is defined as \Delta=g_2^3-27g_3^2...
- Dedekind eta functionDedekind eta functionThe Dedekind eta function, named after Richard Dedekind, is a function defined on the upper half-plane of complex numbers, where the imaginary part is positive...
- J-invariant
Bessel and related functions
- Airy functionAiry functionIn the physical sciences, the Airy function Ai is a special function named after the British astronomer George Biddell Airy...
- Bessel functionBessel functionIn mathematics, Bessel functions, first defined by the mathematician Daniel Bernoulli and generalized by Friedrich Bessel, are canonical solutions y of Bessel's differential equation:...
s: Defined by a differential equationDifferential equationA differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
; useful in astronomyAstronomyAstronomy is a natural science that deals with the study of celestial objects and phenomena that originate outside the atmosphere of Earth...
, electromagnetismElectromagnetismElectromagnetism is one of the four fundamental interactions in nature. The other three are the strong interaction, the weak interaction and gravitation...
, and mechanicsMechanicsMechanics is the branch of physics concerned with the behavior of physical bodies when subjected to forces or displacements, and the subsequent effects of the bodies on their environment....
. - Bessel–Clifford function
- Legendre functionLegendre functionIn mathematics, the Legendre functions Pλ, Qλ and associated Legendre functions P, Q are generalizations of Legendre polynomials to non-integer degree.-Differential equation:...
: From the theory of spherical harmonicsSpherical harmonicsIn mathematics, spherical harmonics are the angular portion of a set of solutions to Laplace's equation. Represented in a system of spherical coordinates, Laplace's spherical harmonics Y_\ell^m are a specific set of spherical harmonics that forms an orthogonal system, first introduced by Pierre...
. - Scorer's function
- Sinc function
- Hermite polynomialsHermite polynomialsIn mathematics, the Hermite polynomials are a classical orthogonal polynomial sequence that arise in probability, such as the Edgeworth series; in combinatorics, as an example of an Appell sequence, obeying the umbral calculus; in numerical analysis as Gaussian quadrature; and in physics, where...
- Chebyshev polynomialsChebyshev polynomialsIn mathematics the Chebyshev polynomials, named after Pafnuty Chebyshev, are a sequence of orthogonal polynomials which are related to de Moivre's formula and which can be defined recursively. One usually distinguishes between Chebyshev polynomials of the first kind which are denoted Tn and...
Riemann zeta and related functions
- Riemann zeta function: A special case of Dirichlet series.
- Dirichlet eta function: An allied function.
- Hurwitz zeta function
- Legendre chi function
- Lerch transcendent
- Polylogarithm and related functions:
- Incomplete polylogarithmIncomplete polylogarithmIn mathematics, the Incomplete Polylogarithm function is related to the polylogarithm function. It is sometimes known as the incomplete Fermi–Dirac integral or the incomplete Bose–Einstein integral...
- Clausen function
- Complete Fermi–Dirac integral, an alternate form of the polylogarithm.
- Incomplete Fermi–Dirac integral
- Kummer's functionKummer's functionIn mathematics, there are several functions known as Kummer's function. One is known as the confluent hypergeometric function of Kummer. Another one, defined below, is related to the polylogarithm...
- Spence's functionSpence's functionIn mathematics, Spence's function, or dilogarithm, denoted as Li2, is a particular case of the polylogarithm. Lobachevsky's function and Clausen's function are closely related functions...
- Incomplete polylogarithm
- Riesz function
Hypergeometric and related functions
- Hypergeometric functions: Versatile family of power series.
- Confluent hypergeometric functionConfluent hypergeometric functionIn mathematics, a confluent hypergeometric function is a solution of a confluent hypergeometric equation, which is a degenerate form of a hypergeometric differential equation where two of the three regular singularities merge into an irregular singularity...
- Associated Legendre functions
- Meijer G-functionMeijer G-FunctionIn mathematics, the G-function was introduced by as a very general function intended to include most of the known special functions as particular cases. This was not the only attempt of its kind: the generalized hypergeometric function and the MacRobert E-function had the same aim, but Meijer's...
Iterated exponential and related functions
- Hyper operators
- Iterated logarithmIterated logarithmIn computer science, the iterated logarithm of n, written n , is the number of times the logarithm function must be iteratively applied before the result is less than or equal to 1...
- PentationPentationPentation is the operation of repeated tetration, just as tetration is the operation of repeated exponentation and is a hyperoperation. It is non-commutative, and therefore has two inverse functions, which might be named the penta-root and the penta-logarithm...
- Super-logarithmSuper-logarithmIn mathematics, the super-logarithm is one of the two inverse functions of tetration. Just as exponentiation has two inverse functions, roots and logarithms, tetration has two inverse functions, super-roots and super-logarithms...
s - Super-roots
- TetrationTetrationIn mathematics, tetration is an iterated exponential and is the next hyper operator after exponentiation. The word tetration was coined by English mathematician Reuben Louis Goodstein from tetra- and iteration. Tetration is used for the notation of very large numbers...
- Lambert W function: Inverse of f(w) = w exp(w).
Other standard special functions
- Lambda function
- Lamé functionLamé functionIn mathematics, a Lamé function is a solution of Lamé's equation, a second-order ordinary differential equation. It was introduced in the paper . Lamé's equation appears in the method of separation of variables applied to the Laplace equation in elliptic coordinates...
- Mittag-Leffler functionMittag-Leffler functionIn mathematics, the Mittag-Leffler function Eα,β is a special function, a complex function which depends on two complex parameters α and β...
- Painlevé transcendentsPainlevé transcendentsIn mathematics, Painlevé transcendents are solutions to certain nonlinear second-order ordinary differential equations in the complex plane with the Painlevé property , but which are not generally solvable in terms of elementary functions...
- Parabolic cylinder function
- Synchrotron function
Miscellaneous functions
- Ackermann functionAckermann functionIn computability theory, the Ackermann function, named after Wilhelm Ackermann, is one of the simplest and earliest-discovered examples of a total computable function that is not primitive recursive...
: in the theory of computationTheory of computationIn theoretical computer science, the theory of computation is the branch that deals with whether and how efficiently problems can be solved on a model of computation, using an algorithm...
, a computable functionComputable functionComputable functions are the basic objects of study in computability theory. Computable functions are the formalized analogue of the intuitive notion of algorithm. They are used to discuss computability without referring to any concrete model of computation such as Turing machines or register...
that is not primitive recursivePrimitive recursive functionThe primitive recursive functions are defined using primitive recursion and composition as central operations and are a strict subset of the total µ-recursive functions...
. - Dirac delta functionDirac delta functionThe Dirac delta function, or δ function, is a generalized function depending on a real parameter such that it is zero for all values of the parameter except when the parameter is zero, and its integral over the parameter from −∞ to ∞ is equal to one. It was introduced by theoretical...
: everywhere zero except for x = 0; total integral is 1. Not a function but a distributionDistribution (mathematics)In mathematical analysis, distributions are objects that generalize functions. Distributions make it possible to differentiate functions whose derivatives do not exist in the classical sense. In particular, any locally integrable function has a distributional derivative...
, but sometimes informally referred to as a function, particularly by physicists and engineers. - Dirichlet function: is an indicator function that matches 1 to rational numbers and 0 to irrationals. It is nowhere continuousNowhere continuousIn mathematics, a nowhere continuous function, also called an everywhere discontinuous function, is a function that is not continuous at any point of its domain...
. - Kronecker delta function: is a function of two variables, usually integers, which is 1 if they are equal, and 0 otherwise.
- Minkowski's question mark functionMinkowski's question mark functionIn mathematics, the Minkowski question mark function, sometimes called the slippery devil's staircase and denoted by ?, is a function possessing various unusual fractal properties, defined by Hermann Minkowski in 1904...
: Derivatives vanish on the rationals. - Weierstrass functionWeierstrass functionIn mathematics, the Weierstrass function is a pathological example of a real-valued function on the real line. The function has the property that it is continuous everywhere but differentiable nowhere...
: is an example of continuous functionContinuous functionIn mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
that is nowhere differentiable
External links
- Special functions : A programmable special functions calculator.
- Special functions at EqWorld: The World of Mathematical Equations.

