A quadratic function, in mathematics

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, is a polynomial function of the form


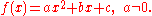
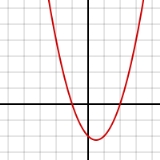
The graph

Graph of a function

In mathematics, the graph of a function f is the collection of all ordered pairs . In particular, if x is a real number, graph means the graphical representation of this collection, in the form of a curve on a Cartesian plane, together with Cartesian axes, etc. Graphing on a Cartesian plane is...

 of a quadratic function is a parabola

Parabola

In mathematics, the parabola is a conic section, the intersection of a right circular conical surface and a plane parallel to a generating straight line of that surface...

 whose axis of symmetry is parallel to the y-axis.

The expression in the definition of a quadratic function is a polynomial of degree

Degree of a polynomial

The degree of a polynomial represents the highest degree of a polynominal's terms , should the polynomial be expressed in canonical form . The degree of an individual term is the sum of the exponents acting on the term's variables...

 2 or second order, or a 2nd degree polynomial, because the highest exponent of x is 2.

If the quadratic function is set equal to zero, then the result is a quadratic equation

Quadratic equation

In mathematics, a quadratic equation is a univariate polynomial equation of the second degree. A general quadratic equation can be written in the formax^2+bx+c=0,\,...

.