
Lamé function
Encyclopedia
In mathematics, a Lamé function (or ellipsoidal harmonic function) is a solution of Lamé's equation, a second-order ordinary differential equation
. It was introduced in the paper . Lamé's equation appears in the method of separation of variables
applied to the Laplace equation in elliptic coordinates
. In some special cases solutions can be expressed in terms of polynomials called Lamé polynomials.
Lamé functions are discussed in detail in
Lamé's equation is
where A and B are constants, and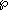 is the Weierstrass elliptic function.
is the Weierstrass elliptic function.
The most important case is when B is of the form n(n + 1) for an integer n, in which case the solutions extend to meromorphic functions defined in the whole complex plane. For other values of B the solutions have branch point
s.
By changing the independent variable, Lamé's equation can also be rewritten in algebraic form as
which after a change of variable becomes a special case of Heun's equation
.
Ordinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
. It was introduced in the paper . Lamé's equation appears in the method of separation of variables
Separation of variables
In mathematics, separation of variables is any of several methods for solving ordinary and partial differential equations, in which algebra allows one to rewrite an equation so that each of two variables occurs on a different side of the equation....
applied to the Laplace equation in elliptic coordinates
Elliptic coordinates
In geometry, the elliptic coordinate system is a two-dimensional orthogonal coordinate system in whichthe coordinate lines are confocal ellipses and hyperbolae...
. In some special cases solutions can be expressed in terms of polynomials called Lamé polynomials.
Lamé functions are discussed in detail in
Lamé's equation is

where A and B are constants, and
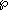 is the Weierstrass elliptic function.
is the Weierstrass elliptic function.The most important case is when B is of the form n(n + 1) for an integer n, in which case the solutions extend to meromorphic functions defined in the whole complex plane. For other values of B the solutions have branch point
Branch point
In the mathematical field of complex analysis, a branch point of a multi-valued function is a point such that the function is discontinuous when going around an arbitrarily small circuit around this point...
s.
By changing the independent variable, Lamé's equation can also be rewritten in algebraic form as

which after a change of variable becomes a special case of Heun's equation
Heun's equation
In mathematics, the local Heun function Hℓ is the solution of Heun's differential equation that is holomorphic and 1 at the singular point z = 0...
.

