
Confluent hypergeometric function
Encyclopedia
In mathematics
, a confluent hypergeometric function is a solution of a confluent hypergeometric equation, which is a degenerate form of a hypergeometric differential equation
where two of the three regular singularities merge into an irregular singularity. (The term "confluent
" refers to the merging of singular points of families of differential equations; "confluere" is Latin for "to flow together".) There are several common standard forms of confluent hypergeometric functions:
The Kummer functions, Whittaker functions, and Coulomb wave functions are essentially the same, and differ from each other only by elementary functions and change of variables.
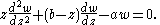 ,
,
with a regular singular point at 0 and an irregular singular point at ∞.
It has two linearly independent solutions M(a,b,z) and U(a,b,z).
Kummer's function (of the first kind) M is a generalized hypergeometric series introduced in , given by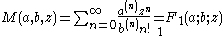
where
is the rising factorial. Another common notation for this solution is Φ(a,b,z). This defines an entire function
of a.b, and z, except for poles at b = 0, −1, − 2, ...
Just as the confluent
differential equation is a limit of the hypergeometric differential equation
as the singular point at 1 is moved towards the singular point at ∞, the confluent hypergeometric function can be given as a limit of the hypergeometric function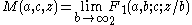
and many of the properties of the confluent hypergeometric function are limiting cases of properties of the hypergeometric function.
Another solution of Kummer's equation is the Tricomi confluent hypergeometric function U(a;b;z) introduced by , and sometimes denoted by Ψ(a;b;.z).
The function U is defined in terms of Kummer's function M by
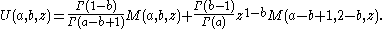
This is undefined for integer b, but can be extended to integer b by continuity.
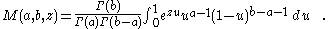
For a with positive real part U can be obtained by the Laplace integral
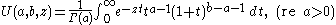
The integral defines a solution in the right half-plane re z > 0.
They can also be represented as Barnes integral
s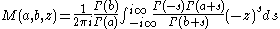
where the contour passes to one side of the poles of Γ(−s) and to the other side of the poles of Γ(a+s).
If z = x is real, then making a change of variables in the integral followed by expanding the binomial series
and integrating it formally term by term gives rise to an asymptotic series expansion, valid as x → ∞: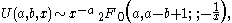
where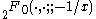 is a generalized hypergeometric series, which converges nowhere but exists as a formal power series
is a generalized hypergeometric series, which converges nowhere but exists as a formal power series
in 1/x.
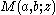 , the four functions
, the four functions 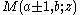 ,
, 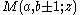 are called contiguous to
are called contiguous to 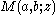 . The function
. The function 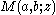 can be written as a linear combination of any two of its contiguous functions, with rational coefficients in terms of
can be written as a linear combination of any two of its contiguous functions, with rational coefficients in terms of  ,
, and
and  . This gives =6 relations, given by identifying any two lines on the right hand side of
. This gives =6 relations, given by identifying any two lines on the right hand side of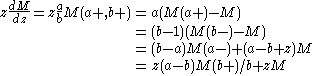
In the notation above,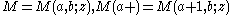 and so on.
and so on.
Repeatedly applying these relations gives a linear relation between any three functions of the form (and their higher derivatives), where
(and their higher derivatives), where  ,
,  are integers.
are integers.
There are similar relations for U.
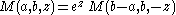
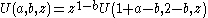 .
.
s hold true: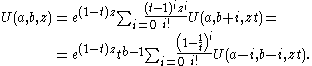
, Kummer's functions have several expansions, for example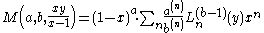
For example, the special case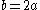 the function reduces to a Bessel function
the function reduces to a Bessel function
:
This identity is sometimes also referred to as Kummer's
second transformation.
Similarly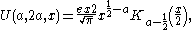
where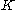 is related to Bessel polynomial for integer
is related to Bessel polynomial for integer  .
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a confluent hypergeometric function is a solution of a confluent hypergeometric equation, which is a degenerate form of a hypergeometric differential equation
Hypergeometric differential equation
In mathematics, the Gaussian or ordinary hypergeometric function 2F1 is a special function represented by the hypergeometric series, that includes many other special functions as specific or limiting cases. It is a solution of a second-order linear ordinary differential equation...
where two of the three regular singularities merge into an irregular singularity. (The term "confluent
Confluence
Confluence, in geography, describes the meeting of two or more bodies of water.Confluence may also refer to:* Confluence , a property of term rewriting systems...
" refers to the merging of singular points of families of differential equations; "confluere" is Latin for "to flow together".) There are several common standard forms of confluent hypergeometric functions:
- Kummer's (confluent hypergeometric) function M(a,b,z), introduced by , is a solution to Kummer's differential equation. There is a different but unrelated Kummer's functionKummer's functionIn mathematics, there are several functions known as Kummer's function. One is known as the confluent hypergeometric function of Kummer. Another one, defined below, is related to the polylogarithm...
bearing the same name. - Tricomi's (confluent hypergeometric) function U(a;b;z) introduced by , sometimes denoted by Ψ(a;b;.z), is another solution to Kummer's equation.
- Whittaker functionWhittaker functionIn mathematics, a Whittaker function is a special solution of Whittaker's equation, a modified form of the confluent hypergeometric equation introduced by to make the formulas involving the solutions more symmetric...
s (for Edmund Taylor Whittaker) are solutions to Whittaker's equation. - Coulomb wave functionCoulomb wave functionIn mathematics, a Coulomb wave function is a solution of the Coulomb wave equation, named after Charles-Augustin de Coulomb. They are used to describe the behavior of charged particles in a Coulomb potential and can be written in terms of confluent hypergeometric functions or Whittaker functions of...
s are solutions to Coulomb wave equation.
The Kummer functions, Whittaker functions, and Coulomb wave functions are essentially the same, and differ from each other only by elementary functions and change of variables.
Kummer's equation
Kummer's equation is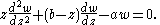 ,
,with a regular singular point at 0 and an irregular singular point at ∞.
It has two linearly independent solutions M(a,b,z) and U(a,b,z).
Kummer's function (of the first kind) M is a generalized hypergeometric series introduced in , given by
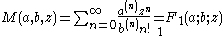
where
is the rising factorial. Another common notation for this solution is Φ(a,b,z). This defines an entire function
Entire function
In complex analysis, an entire function, also called an integral function, is a complex-valued function that is holomorphic over the whole complex plane...
of a.b, and z, except for poles at b = 0, −1, − 2, ...
Just as the confluent
differential equation is a limit of the hypergeometric differential equation
Hypergeometric differential equation
In mathematics, the Gaussian or ordinary hypergeometric function 2F1 is a special function represented by the hypergeometric series, that includes many other special functions as specific or limiting cases. It is a solution of a second-order linear ordinary differential equation...
as the singular point at 1 is moved towards the singular point at ∞, the confluent hypergeometric function can be given as a limit of the hypergeometric function
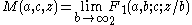
and many of the properties of the confluent hypergeometric function are limiting cases of properties of the hypergeometric function.
Another solution of Kummer's equation is the Tricomi confluent hypergeometric function U(a;b;z) introduced by , and sometimes denoted by Ψ(a;b;.z).
The function U is defined in terms of Kummer's function M by
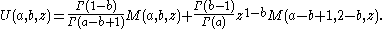
This is undefined for integer b, but can be extended to integer b by continuity.
Integral representations
If Re b > Re a > 0, M(a,b,z) can be represented as an integral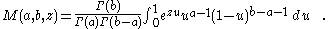
For a with positive real part U can be obtained by the Laplace integral
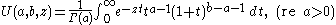
The integral defines a solution in the right half-plane re z > 0.
They can also be represented as Barnes integral
Barnes integral
In mathematics, a Barnes integral or Mellin–Barnes integral is a contour integral involving a product of gamma functions. They were introduced by...
s
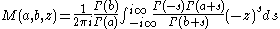
where the contour passes to one side of the poles of Γ(−s) and to the other side of the poles of Γ(a+s).
Asymptotic behavior
The asymptotic behavior of U(a,b,z) as z → ∞ can be deduced from the integral representations.If z = x is real, then making a change of variables in the integral followed by expanding the binomial series
Binomial series
In mathematics, the binomial series is the Taylor series at x = 0 of the function f given by f = α, where is an arbitrary complex number...
and integrating it formally term by term gives rise to an asymptotic series expansion, valid as x → ∞:
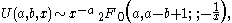
where
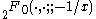 is a generalized hypergeometric series, which converges nowhere but exists as a formal power series
is a generalized hypergeometric series, which converges nowhere but exists as a formal power seriesFormal power series
In mathematics, formal power series are a generalization of polynomials as formal objects, where the number of terms is allowed to be infinite; this implies giving up the possibility to substitute arbitrary values for indeterminates...
in 1/x.
Relations
There are many relations between Kummer functions for various arguments and their derivatives. This section gives a few typical examples.Contiguous relations
Given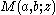 , the four functions
, the four functions 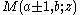 ,
, 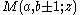 are called contiguous to
are called contiguous to 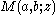 . The function
. The function 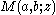 can be written as a linear combination of any two of its contiguous functions, with rational coefficients in terms of
can be written as a linear combination of any two of its contiguous functions, with rational coefficients in terms of  ,
, and
and  . This gives =6 relations, given by identifying any two lines on the right hand side of
. This gives =6 relations, given by identifying any two lines on the right hand side of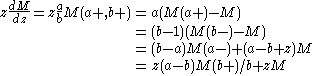
In the notation above,
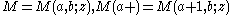 and so on.
and so on.Repeatedly applying these relations gives a linear relation between any three functions of the form
 (and their higher derivatives), where
(and their higher derivatives), where  ,
,  are integers.
are integers.There are similar relations for U.
Kummer's transformation
Kummer's functions are also related by Kummer's transformations: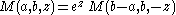
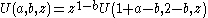 .
.Multiplication theorem
The following multiplication theoremMultiplication theorem
In mathematics, the multiplication theorem is a certain type of identity obeyed by many special functions related to the gamma function. For the explicit case of the gamma function, the identity is a product of values; thus the name...
s hold true:
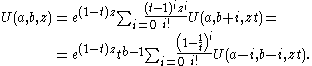
Connection with Laguerre polynomials and similar representations
In terms of Laguerre polynomialsLaguerre polynomials
In mathematics, the Laguerre polynomials, named after Edmond Laguerre ,are the canonical solutions of Laguerre's equation:x\,y + \,y' + n\,y = 0\,which is a second-order linear differential equation....
, Kummer's functions have several expansions, for example
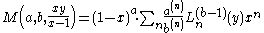
Special cases
Functions that can be expressed as special cases of the confluent hypergeometric function include:- Bateman's function
- Bessel functionBessel functionIn mathematics, Bessel functions, first defined by the mathematician Daniel Bernoulli and generalized by Friedrich Bessel, are canonical solutions y of Bessel's differential equation:...
s and many related functions such as Airy functionAiry functionIn the physical sciences, the Airy function Ai is a special function named after the British astronomer George Biddell Airy...
s, Kelvin functions, Hankel functions.
For example, the special case
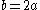 the function reduces to a Bessel function
the function reduces to a Bessel functionBessel function
In mathematics, Bessel functions, first defined by the mathematician Daniel Bernoulli and generalized by Friedrich Bessel, are canonical solutions y of Bessel's differential equation:...
:

This identity is sometimes also referred to as Kummer's
Ernst Kummer
Ernst Eduard Kummer was a German mathematician. Skilled in applied mathematics, Kummer trained German army officers in ballistics; afterwards, he taught for 10 years in a gymnasium, the German equivalent of high school, where he inspired the mathematical career of Leopold Kronecker.-Life:Kummer...
second transformation.
Similarly
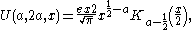
where
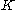 is related to Bessel polynomial for integer
is related to Bessel polynomial for integer  .
.
- The error functionError functionIn mathematics, the error function is a special function of sigmoid shape which occurs in probability, statistics and partial differential equations...
can be expressed as
-
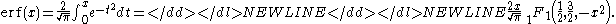
- Coulomb wave functionCoulomb wave functionIn mathematics, a Coulomb wave function is a solution of the Coulomb wave equation, named after Charles-Augustin de Coulomb. They are used to describe the behavior of charged particles in a Coulomb potential and can be written in terms of confluent hypergeometric functions or Whittaker functions of...
- Cunningham functionCunningham functionIn statistics, the Cunningham function or Pearson–Cunningham function ωm,n is a generalisation of a special function introduced by and studied in the form here by...
s - Elementary functions such as sin, cos, exp. For example,
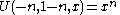
- Exponential integralExponential integralIn mathematics, the exponential integral is a special function defined on the complex plane given the symbol Ei.-Definitions:For real, nonzero values of x, the exponential integral Ei can be defined as...
and related functions such as the sine integral, logarithmic integral - Hermite polynomialsHermite polynomialsIn mathematics, the Hermite polynomials are a classical orthogonal polynomial sequence that arise in probability, such as the Edgeworth series; in combinatorics, as an example of an Appell sequence, obeying the umbral calculus; in numerical analysis as Gaussian quadrature; and in physics, where...
- Incomplete gamma functionIncomplete gamma functionIn mathematics, the gamma function is defined by a definite integral. The incomplete gamma function is defined as an integral function of the same integrand. There are two varieties of the incomplete gamma function: the upper incomplete gamma function is for the case that the lower limit of...
- Laguerre polynomialsLaguerre polynomialsIn mathematics, the Laguerre polynomials, named after Edmond Laguerre ,are the canonical solutions of Laguerre's equation:x\,y + \,y' + n\,y = 0\,which is a second-order linear differential equation....
- Parabolic cylinder function (or Weber function)
- Poisson–Charlier function
- Toronto functions
- Whittaker functionWhittaker functionIn mathematics, a Whittaker function is a special solution of Whittaker's equation, a modified form of the confluent hypergeometric equation introduced by to make the formulas involving the solutions more symmetric...
s Mκ,μ(z), Wκ,μ(z) are solutions of Whittaker's equation that can be expressed in terms of Kummer functions M and U by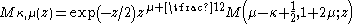
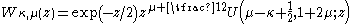
- The general p-th raw moment (p not necessarily an integer) can be expressed as
-
-
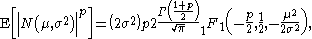
-
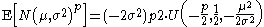 (the function's second branch cut can be chosen by multiplying with
(the function's second branch cut can be chosen by multiplying with 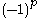 ).
).
-
Application to continued fractions
By applying a limiting argument to Gauss's continued fraction it can be shown that
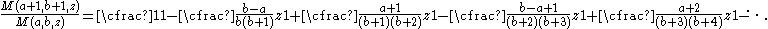
and that this continued fraction converges uniformly to a meromorphic function of z in every bounded domain that does not include a pole.
External links
- Kummer hypergeometric function on the Wolfram Functions site
- Tricomi hypergeometric function on the Wolfram Functions site
- Coulomb wave function


