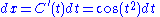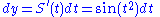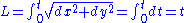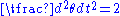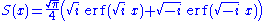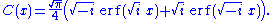Fresnel integral - AbsoluteAstronomy.com

Fresnel integrals, S(x) and C(x), are two transcendental function

Transcendental function

A transcendental function is a function that does not satisfy a polynomial equation whose coefficients are themselves polynomials, in contrast to an algebraic function, which does satisfy such an equation...

s named after Augustin-Jean Fresnel

Augustin-Jean Fresnel

Augustin-Jean Fresnel , was a French engineer who contributed significantly to the establishment of the theory of wave optics. Fresnel studied the behaviour of light both theoretically and experimentally....

that are used in optics

Optics

Optics is the branch of physics which involves the behavior and properties of light, including its interactions with matter and the construction of instruments that use or detect it. Optics usually describes the behavior of visible, ultraviolet, and infrared light...

. They arise in the description of near field

Near field

Near field may refer to:*Near-field , an algebraic structure*Near and far field, parts of an electromagnetic field*Near field communication, a set of short-range wireless technologies, typically requiring a distance of 4 cm or less...

Fresnel diffraction

In optics, the Fresnel diffraction equation for near-field diffraction, is an approximation of Kirchhoff-Fresnel diffraction that can be applied to the propagation of waves in the near field....

phenomena, and are defined through the following integral

Integral

Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...

representations:

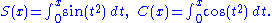
The simultaneous parametric plot

Parametric equation

In mathematics, parametric equation is a method of defining a relation using parameters. A simple kinematic example is when one uses a time parameter to determine the position, velocity, and other information about a body in motion....

of S(x) and C(x) is the Euler spiral

Euler spiral

An Euler spiral is a curve whose curvature changes linearly with its curve length . Euler spirals are also commonly referred to as spiros, clothoids or Cornu spirals....

, also known as the Cornu spiral or clothoid.

Definition

The Fresnel integrals admit the following power series expansions that converge for all x:

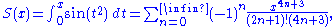
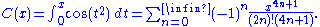
Some authors, including Abramowitz and Stegun

Abramowitz and Stegun

Abramowitz and Stegun is the informal name of a mathematical reference work edited by Milton Abramowitz and Irene Stegun of the U.S. National Bureau of Standards...

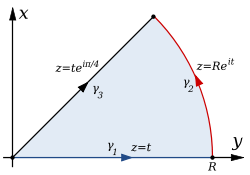
, (eqs 7.3.1 – 7.3.2) use

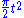for the argument of the integrals defining S(x) and C(x). To get these functions, multiply the above integrals by

and divide the argument x by the same factor.

Euler spiral

The Euler spiral
Spiral
In mathematics, a spiral is a curve which emanates from a central point, getting progressively farther away as it revolves around the point.-Spiral or helix:...

, also known as Cornu spiral or clothoid, is the curve generated by a parametric plot of S(t) against C(t). The Cornu spiral was created by Marie Alfred Cornu

Marie Alfred Cornu

Marie Alfred Cornu was a French physicist. The French generally refer to him as Alfred Cornu.Cornu was born at Orléans and was educated at the École polytechnique and the École des mines...

as a nomogram

Nomogram

A nomogram, nomograph, or abac is a graphical calculating device developed by P.E. Elyasberg, a two-dimensional diagram designed to allow the approximate graphical computation of a function: it uses a coordinate system other than Cartesian coordinates...

for diffraction computations in science and engineering.

From the definitions of Fresnel integrals, the infinitesimals dx and dy are thus:

Thus the length of the spiral measured from the origin can be expressed as:

That is, the parameter is the curve length measured from the origin (0,0) and the Euler spiral has infinite length. The vector also expresses the unit tangent vector

Tangent vector

A tangent vector is a vector that is tangent to a curve or surface at a given point.Tangent vectors are described in the differential geometry of curves in the context of curves in Rn. More generally, tangent vectors are elements of a tangent space of a differentiable manifold....

along the spiral, giving θ = . Since t is the curve length, the curvature,

can be expressed as:

And the rate of change of curvature with respect to the curve length is:

An Euler spiral has the property that its curvature

Curvature

In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...

at any point is proportional to the distance along the spiral, measured from the origin. This property makes it useful as a transition curve

Track transition curve

A track transition curve, or spiral easement, is a mathematically calculated curve on a section of highway, or railroad track, where a straight section changes into a curve. It is designed to prevent sudden changes in centripetal force...

in highway and railway engineering.

If a vehicle follows the spiral at unit speed, the parameter in the above derivatives also represents the time. That is, a vehicle following the spiral at constant speed will have a constant rate of angular acceleration

Angular acceleration

Angular acceleration is the rate of change of angular velocity over time. In SI units, it is measured in radians per second squared , and is usually denoted by the Greek letter alpha .- Mathematical definition :...

.

Sections from Euler spirals are commonly incorporated into the shape of roller-coaster loops to make what are known as "clothoid loops".

Properties

C(x) and S(x) are odd functions of x.
C and S are entire function
Entire function
In complex analysis, an entire function, also called an integral function, is a complex-valued function that is holomorphic over the whole complex plane...

s.
Using the power series expansions above, the Fresnel integrals can be extended to the domain of complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...

s, and they become analytic function
Analytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...

s of a complex variable. The Fresnel integrals can be expressed using the error function
Error function
In mathematics, the error function is a special function of sigmoid shape which occurs in probability, statistics and partial differential equations...

as follows:

The integrals defining C(x) and S(x) cannot be evaluated in the closed form
Closed-form expression
In mathematics, an expression is said to be a closed-form expression if it can be expressed analytically in terms of a bounded number of certain "well-known" functions...

in terms of elementary functions, except in special cases. The limits
Limit of a function
In mathematics, the limit of a function is a fundamental concept in calculus and analysis concerning the behavior of that function near a particular input....

of these functions as x goes to infinity are known:

Evaluation

The limits of C and S as the argument tends to infinity can be found by the methods of complex analysis

Complex analysis

Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...

. This uses the contour integral of the function

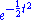
around the boundary of the sector

Circular sector

A circular sector or circle sector, is the portion of a disk enclosed by two radii and an arc, where the smaller area is known as the minor sector and the larger being the major sector. In the diagram, θ is the central angle in radians, r the radius of the circle, and L is the arc length of the...

-shaped region in the complex plane

Complex plane

In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...

formed by the positive x-axis, the half-line y = x, x ≥ 0, and the circle of radius R centered at the origin.

As R goes to infinity, the integral along the circular arc tends to 0, the integral along the real axis tends to the Gaussian integral

Gaussian integral

The Gaussian integral, also known as the Euler-Poisson integral or Poisson integral, is the integral of the Gaussian function e−x2 over the entire real line.It is named after the German mathematician and...

and after routine transformations, the integral along the bisector of the first quadrant can be related to the limit of the Fresnel integrals.

Generalization

The Fresnel integral can be generalized by the function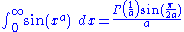

with the left-hand side converging for a>1 and the right-hand side being its analytical extension to the whole plane less where lie the poles of

Definition

Euler spiral

Properties

Evaluation

Generalization

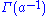See also