Iterated logarithm
Encyclopedia
In computer science
, the iterated logarithm of n, written n (usually read "log star"), is the number of times the logarithm
function must be iteratively applied before the result is less than or equal to 1. The simplest formal definition is the result of this recursive function:
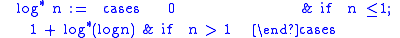
On the positive real numbers, the continuous super-logarithm
(inverse tetration
) is essentially equivalent: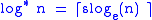
but on the negative real numbers, log-star is 0, whereas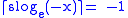
for positive x, so the two functions differ for negative arguments.
In computer science, is often used to indicate the binary iterated logarithm, which iterates the binary logarithm
instead. The iterated logarithm accepts any positive real number
and yields an integer
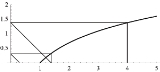
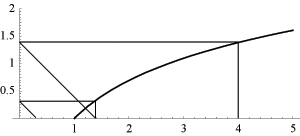
. Graphically, it can be understood as the number of "zig-zags" needed in Figure 1 to reach the interval [0, 1] on the x-axis.
Mathematically, the iterated logarithm is well-defined not only for base 2 and base e, but for any base greater than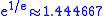
.
The iterated logarithm is closely related to the generalized logarithm function used in symmetric level-index arithmetic
. It is also proportional to the additive persistence of a number
, the number of times one must replace the number by the sum of its digits before reaching its digital root
.
and computational complexity
, appearing in the time and space complexity bounds of some algorithms such as:
The iterated logarithm grows at an extremely slow rate, much slower than the logarithm itself. For all values of n relevant to counting the running times of algorithms implemented in practice (i.e., n ≤ 265536, which is far more than the number of particles in the known universe), the iterated logarithm with base 2 has a value no more than 5.
Higher bases give smaller iterated logarithms. Indeed, the only function commonly used in complexity theory that grows more slowly is the inverse Ackermann function.
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
, the iterated logarithm of n, written n (usually read "log star"), is the number of times the logarithm
Logarithm
The logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
function must be iteratively applied before the result is less than or equal to 1. The simplest formal definition is the result of this recursive function:
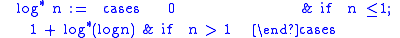
On the positive real numbers, the continuous super-logarithm
Super-logarithm
In mathematics, the super-logarithm is one of the two inverse functions of tetration. Just as exponentiation has two inverse functions, roots and logarithms, tetration has two inverse functions, super-roots and super-logarithms...
(inverse tetration
Tetration
In mathematics, tetration is an iterated exponential and is the next hyper operator after exponentiation. The word tetration was coined by English mathematician Reuben Louis Goodstein from tetra- and iteration. Tetration is used for the notation of very large numbers...
) is essentially equivalent:
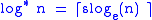
but on the negative real numbers, log-star is 0, whereas
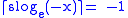for positive x, so the two functions differ for negative arguments.Binary logarithm
In mathematics, the binary logarithm is the logarithm to the base 2. It is the inverse function of n ↦ 2n. The binary logarithm of n is the power to which the number 2 must be raised to obtain the value n. This makes the binary logarithm useful for anything involving powers of 2,...
instead. The iterated logarithm accepts any positive real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
and yields an integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
. Graphically, it can be understood as the number of "zig-zags" needed in Figure 1 to reach the interval [0, 1] on the x-axis.
Mathematically, the iterated logarithm is well-defined not only for base 2 and base e, but for any base greater than
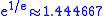.The iterated logarithm is closely related to the generalized logarithm function used in symmetric level-index arithmetic
Symmetric level-index arithmetic
The level-index representation of numbers, and its algorithms for arithmetic operations, were introduced by Clenshaw & Olver. The symmetric form of the LI system and its arithmetic operations were presented by Clenshaw & Turner. Anuta, Lozier, Schabanel and Turner developed the algorithm for...
. It is also proportional to the additive persistence of a number
Persistence of a number
In mathematics, the persistence of a number is a term used to describe the number of times one must apply a given operation to an integer before reaching a fixed point, i.e...
, the number of times one must replace the number by the sum of its digits before reaching its digital root
Digital root
The digital root of a number is the value obtained by an iterative process of summing digits, on each iteration using the result from the previous iteration to compute a digit sum...
.
Analysis of algorithms
The iterated logarithm is useful in analysis of algorithmsAnalysis of algorithms
To analyze an algorithm is to determine the amount of resources necessary to execute it. Most algorithms are designed to work with inputs of arbitrary length...
and computational complexity
Computational Complexity
Computational Complexity may refer to:*Computational complexity theory*Computational Complexity...
, appearing in the time and space complexity bounds of some algorithms such as:
- Finding the Delaunay triangulationDelaunay triangulationIn mathematics and computational geometry, a Delaunay triangulation for a set P of points in a plane is a triangulation DT such that no point in P is inside the circumcircle of any triangle in DT. Delaunay triangulations maximize the minimum angle of all the angles of the triangles in the...
of a set of points knowing the Euclidean minimum spanning treeEuclidean minimum spanning treeThe Euclidean minimum spanning tree or EMST is a minimum spanning tree of a set of n points in the plane , where the weight of the edge between each pair of points is the distance between those two points...
: randomized O(n n) time, Olivier Devillers - Fürer's algorithm for integer multiplication: O(n log n 2 n)
- Finding an approximate maximum (element at least as large as the median): n − 4 to n + 2 parallel operations
- Richard Cole and Uzi VishkinUzi VishkinUzi Vishkin is a computer scientist at the University of Maryland, College Park, where he is Professor of Electrical and Computer Engineering at the University of Maryland Institute for Advanced Computer Studies . Uzi Vishkin is known for his work in the field of parallel computing...
's distributed algorithm for 3-coloring an n-cycle: O( n) synchronous communication rounds.
The iterated logarithm grows at an extremely slow rate, much slower than the logarithm itself. For all values of n relevant to counting the running times of algorithms implemented in practice (i.e., n ≤ 265536, which is far more than the number of particles in the known universe), the iterated logarithm with base 2 has a value no more than 5.
| x | x |
|---|---|
| (−∞, 1] | 0 |
| (1, 2] | 1 |
| (2, 4] | 2 |
| (4, 16] | 3 |
| (16, 65536] | 4 |
| (65536, 265536] | 5 |
Higher bases give smaller iterated logarithms. Indeed, the only function commonly used in complexity theory that grows more slowly is the inverse Ackermann function.