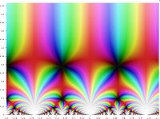
J-invariant
Encyclopedia
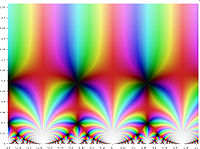
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Klein's
Felix Klein
Christian Felix Klein was a German mathematician, known for his work in group theory, function theory, non-Euclidean geometry, and on the connections between geometry and group theory...
j-invariant, regarded as a function of a complex variable
Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
τ, is a modular function defined on the upper half-plane of complex numbers.
We have
The modular discriminant
 is defined as
is defined as
The numerator and denominator above are in terms of the modular invariant
Modular invariant
In mathematics, a modular invariant may be* A modular invariant of a group acting on a vector space of positive characteristic* The elliptic modular function, giving the modular invariant of an elliptic curve....
s
 and
and  of the Weierstrass elliptic functions
of the Weierstrass elliptic functions
and the modular discriminant.
These have the properties that

 one of weight four, so that its third power is also of weight twelve. The quotient is therefore a modular function of weight zero; this means j has the absolutely invariant property that
one of weight four, so that its third power is also of weight twelve. The quotient is therefore a modular function of weight zero; this means j has the absolutely invariant property thatExpressions in terms of theta functions
We can express it in terms of Jacobi's theta functions, in which form it can very rapidly be computed.
The fundamental region
The two transformations and
and  together generate a group
together generate a groupGroup (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
called the modular group
Modular group
In mathematics, the modular group Γ is a fundamental object of study in number theory, geometry, algebra, and many other areas of advanced mathematics...
, which we may identify with the projective special linear group
 . By a suitable choice of transformation belonging to this group,
. By a suitable choice of transformation belonging to this group, , with ad − bc = 1, we may reduce τ to a value giving the same value for j, and lying in the fundamental region for j, which consists of values for τ satisfying the conditions
, with ad − bc = 1, we may reduce τ to a value giving the same value for j, and lying in the fundamental region for j, which consists of values for τ satisfying the conditionsThe function j(τ) takes on every value in the complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s
 exactly once in this region. In other words, for every
exactly once in this region. In other words, for every , there is a τ in the fundamental region such that c=j(τ). Thus, j has the property of mapping the fundamental region to the entire complex plane, and vice-versa.
, there is a τ in the fundamental region such that c=j(τ). Thus, j has the property of mapping the fundamental region to the entire complex plane, and vice-versa.As a Riemann surface, the fundamental region has genus 0, and every (level one) modular function is a rational function
Rational function
In mathematics, a rational function is any function which can be written as the ratio of two polynomial functions. Neither the coefficients of the polynomials nor the values taken by the function are necessarily rational.-Definitions:...
in j; and, conversely, every rational function in j is a modular function. In other words the field of modular functions is
 .
.The values of j are in a one-to-one relationship with values of τ lying in the fundamental region, and each value for j corresponds to the field of elliptic function
Elliptic function
In complex analysis, an elliptic function is a function defined on the complex plane that is periodic in two directions and at the same time is meromorphic...
s with periods 1 and τ, for the corresponding value of τ; this means that j is in a one-to-one relationship with isomorphism classes of elliptic curve
Elliptic curve
In mathematics, an elliptic curve is a smooth, projective algebraic curve of genus one, on which there is a specified point O. An elliptic curve is in fact an abelian variety — that is, it has a multiplication defined algebraically with respect to which it is a group — and O serves as the identity...
s over the complex numbers.
Class field theory and j
The j-invariant has many remarkable properties. One of these is that if τ is any element of an imaginary quadratic fieldQuadratic field
In algebraic number theory, a quadratic field is an algebraic number field K of degree two over Q. It is easy to show that the map d ↦ Q is a bijection from the set of all square-free integers d ≠ 0, 1 to the set of all quadratic fields...
with positive imaginary part (so that j is defined) then
 is an algebraic integer
is an algebraic integerAlgebraic integer
In number theory, an algebraic integer is a complex number that is a root of some monic polynomial with coefficients in . The set of all algebraic integers is closed under addition and multiplication and therefore is a subring of complex numbers denoted by A...
. The field extension

is abelian, meaning with abelian Galois group
Galois group
In mathematics, more specifically in the area of modern algebra known as Galois theory, the Galois group of a certain type of field extension is a specific group associated with the field extension...
. We have a lattice in the complex plane defined by 1 and τ, and it is easy to see that all of the elements of the
field
 which send lattice points to other lattice points under multiplication form a ring with units, called an order. The other lattices with generators 1 and τ' associated in like manner to the same order define the algebraic conjugates
which send lattice points to other lattice points under multiplication form a ring with units, called an order. The other lattices with generators 1 and τ' associated in like manner to the same order define the algebraic conjugates  of
of  over
over  . The unique maximal order under inclusion of
. The unique maximal order under inclusion of  is the ring of algebraic integers of
is the ring of algebraic integers of  , and values of τ having it as its associated order lead to unramified extensions of
, and values of τ having it as its associated order lead to unramified extensions of  . These classical results are the starting point for the theory of complex multiplication
. These classical results are the starting point for the theory of complex multiplicationComplex multiplication
In mathematics, complex multiplication is the theory of elliptic curves E that have an endomorphism ring larger than the integers; and also the theory in higher dimensions of abelian varieties A having enough endomorphisms in a certain precise sense In mathematics, complex multiplication is the...
.
Transcendence properties
In 1937 Theodor SchneiderTheodor Schneider
Theodor Schneider was a German mathematician, best known for providing proof of what is now known as the Gelfond–Schneider theorem in 1935....
proved the aforementioned result that if
 is a quadratic irrational number in the upper half plane then j(
is a quadratic irrational number in the upper half plane then j( ) is an algebraic integer. In addition he proved that if
) is an algebraic integer. In addition he proved that if  is an algebraic number
is an algebraic numberAlgebraic number
In mathematics, an algebraic number is a number that is a root of a non-zero polynomial in one variable with rational coefficients. Numbers such as π that are not algebraic are said to be transcendental; almost all real numbers are transcendental...
but not imaginary quadratic then j(
 ) is transcendental.
) is transcendental.The j function has numerous other transcendental properties. Kurt Mahler
Kurt Mahler
Kurt Mahler was a mathematician and Fellow of the Royal Society.He was a student at the universities in Frankfurt and Göttingen, graduating with a Ph.D...
conjectured a particular transcendence result that is often referred to as Mahler's conjecture, though it was proved as a corollary of results by Yu. V. Nesternko and Patrice Phillipon in the 1990s. Mahler's conjecture was that the if
 was in the upper half plane then exp(2πi
was in the upper half plane then exp(2πi ) and j(
) and j( ) were never both simultaneously algebraic. Stronger results are now known, for example if exp(2πi
) were never both simultaneously algebraic. Stronger results are now known, for example if exp(2πi ) is algebraic then the following three numbers are algebraically independent, and thus transcendental:
) is algebraic then the following three numbers are algebraically independent, and thus transcendental:
The q-expansion and moonshine
Several remarkable properties of j have to do with its q-expansion (Fourier seriesFourier series
In mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
expansion, written as a Laurent series
Laurent series
In mathematics, the Laurent series of a complex function f is a representation of that function as a power series which includes terms of negative degree. It may be used to express complex functions in cases where...
in terms of
 ), which begins:
), which begins:
Note that j has a simple pole at the cusp, so its q-expansion has no terms below
 .
.All the Fourier coefficients are integers, which results in several almost integers, notably Ramanujan's constant :
 .
.Moonshine
More remarkably, the Fourier coefficients for the positive exponents of q are the dimensions of the graded part of an infinite-dimensional graded algebra representation of the monster groupMonster group
In the mathematical field of group theory, the Monster group M or F1 is a group of finite order:...
called the moonshine module – specifically, the coefficient of
 is the dimension of grade-n part of the moonshine module, the first example being the Griess algebra
is the dimension of grade-n part of the moonshine module, the first example being the Griess algebraGriess algebra
In mathematics, the Griess algebra is a commutative non-associative algebra on a real vector space of dimension 196884 that has the Monster group M as its automorphism group. It is named after mathematician R. L. Griess, who constructed it in 1980 and subsequently used it in 1982 to construct M...
, which has dimension 196,884, corresponding to the term
 This startling observation was the starting point for moonshine theory.
This startling observation was the starting point for moonshine theory.The study of the Moonshine conjecture led J.H. Conway and Simon P. Norton
Simon P. Norton
Simon Phillips Norton is a mathematician in Cambridge, England, who works on finite simple groups. He constructed the Harada–Norton group, and in 1979 together with John Conway proved there is a connection between the Monster group and the j-function in number theory. They dubbed this monstrous...
to look at the genus-zero modular functions. If they are normalized to have the form

then Thompson
John G. Thompson
John Griggs Thompson is a mathematician at the University of Florida noted for his work in the field of finite groups. He was awarded the Fields Medal in 1970, the Wolf Prize in 1992 and the 2008 Abel Prize....
showed that there are only a finite number of such functions (of some finite level), and Cummins
later showed that there are exactly 6486 of them, 616 of which have integral coefficients..
A remarkable property of the q-series for j is the product formula; if p and q are small enough we have
Algebraic definition
So far we have been considering j as a function of a complex variable. However, as an invariant for isomorphism classes of elliptic curves, it can be defined purely algebraically. Let
be a plane elliptic curve over any field. Then we may define



and
the latter expression is the discriminant
Discriminant
In algebra, the discriminant of a polynomial is an expression which gives information about the nature of the polynomial's roots. For example, the discriminant of the quadratic polynomialax^2+bx+c\,is\Delta = \,b^2-4ac....
of the curve.
The j-invariant for the elliptic curve may now be defined as

In the case that the field over which the curve is defined has characteristic different from 2 or 3, this definition can also be written as

Inverse and special values
The inverse of the j-invariant can be expressed in terms of the hypergeometric function (see main article Picard–Fuchs equation). The inversion of the j-invariant was reported by Semjon Adlaj (CCRAS, Moscow, Russia) on May 30, 2011 prior to a talk given at the 14-TH WORKSHOP ON COMPUTER ALGEBRA (Dubna, Russia). The inversion is highly relevant to applications via enabling high precision calculations of elliptic functions periods even as their ratios become unbounded. A related result is the expressability via quadratic radicals of the values of j at the points of the imaginary axis whose magnitudes are powers of 2 (thus permitting compass and straightedge constructions). The latter result is hardly evident since the modular equation
(see main article Picard–Fuchs equation). The inversion of the j-invariant was reported by Semjon Adlaj (CCRAS, Moscow, Russia) on May 30, 2011 prior to a talk given at the 14-TH WORKSHOP ON COMPUTER ALGEBRA (Dubna, Russia). The inversion is highly relevant to applications via enabling high precision calculations of elliptic functions periods even as their ratios become unbounded. A related result is the expressability via quadratic radicals of the values of j at the points of the imaginary axis whose magnitudes are powers of 2 (thus permitting compass and straightedge constructions). The latter result is hardly evident since the modular equationModular equation
In mathematics, a modular equation is an algebraic equation satisfied by moduli, in the sense of moduli problem. That is, given a number of functions on a moduli space, a modular equation is an equation holding between them, or in other words an identity for moduli.The most frequent use of the term...
of level 2 is cubic. For example, the value of j at
 simplifies(!) to:
simplifies(!) to:
The j-invariant vanishes at the "corner" of the fundamental domain
Fundamental domain
In geometry, the fundamental domain of a symmetry group of an object is a part or pattern, as small or irredundant as possible, which determines the whole object based on the symmetry. More rigorously, given a topological space and a group acting on it, the images of a single point under the group...
at
 . Here are seven more special values (only the first four of which are well known):
. Here are seven more special values (only the first four of which are well known):













