
Divisor
Overview
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a divisor of an integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
 , also called a factor of
, also called a factor of  , is an integer which divides
, is an integer which divides  without leaving a remainder
without leaving a remainderRemainder
In arithmetic, the remainder is the amount "left over" after the division of two integers which cannot be expressed with an integer quotient....
.
The name "divisor" comes from the arithmetic
Arithmetic
Arithmetic or arithmetics is the oldest and most elementary branch of mathematics, used by almost everyone, for tasks ranging from simple day-to-day counting to advanced science and business calculations. It involves the study of quantity, especially as the result of combining numbers...
operation of division
Division (mathematics)
right|thumb|200px|20 \div 4=5In mathematics, especially in elementary arithmetic, division is an arithmetic operation.Specifically, if c times b equals a, written:c \times b = a\,...
: if
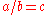 then
then  is the dividend
is the dividendDivision (mathematics)
right|thumb|200px|20 \div 4=5In mathematics, especially in elementary arithmetic, division is an arithmetic operation.Specifically, if c times b equals a, written:c \times b = a\,...
,
 the divisor, and
the divisor, and  the quotient
the quotientQuotient
In mathematics, a quotient is the result of division. For example, when dividing 6 by 3, the quotient is 2, while 6 is called the dividend, and 3 the divisor. The quotient further is expressed as the number of times the divisor divides into the dividend e.g. The quotient of 6 and 2 is also 3.A...
.
In general, for non-zero integers
 and
and  ,
,  divides
divides  , written:
, written: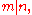
if there exists an integer
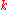 such that
such that  .
.
Unanswered Questions
Discussions

