
List of types of functions
Encyclopedia
Functions can be classified according to the properties they have. These properties describe the functions behaviour under certain conditions. A parabola is a specific type of function.
Relative to set theory
These properties concern the domain
, the codomain
and the range
of functions.
Relative to an operator (c.q. a group
These properties concern how the function is affected by arithmetic
operations on its operand.
The following are special examples of a homomorphism
on a binary operation
:
Relative to negation
:
Relative to a binary operation and an order
:
In general, functions are often defined by specifying the name of a dependent variable, and a way of calculating what it should map to. For this purpose, the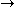 symbol or Church
symbol or Church
's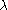
is often used. Also, sometimes mathematicians notate a function's domain
and codomain
by writing e.g. . These notions extend directly to lambda calculus
. These notions extend directly to lambda calculus
and type theory
, respectively.
is a branch of mathematics that formalizes the notion of a special function via arrows or morphisms. A category
is an algebraic object that (abstractly) consists of a class of objects, and for every pair of objects, a set of morphisms. A partial (equiv. dependently typed) binary operation called composition
is provided on morphisms, every object has one special morphism from it to itself called the identity
on that object, and composition and identities are required to obey certain relations.
In a so-called concrete category
, the objects are associated with mathematical structures like sets, magmas, groups
, rings
, topological spaces, vector spaces, metric spaces, partial orders
, differentiable manifolds, uniform spaces, etc., and morphisms between two objects are associated with structure-preserving functions between them. In the examples above, these would be functions
, magma homomorphisms, group homomorphisms, ring homomorphisms, continuous functions, linear transformations (or matrices
), metric maps, monotonic function
s, differentiable functions, and uniformly continuous functions, respectively.
As an algebraic theory, one of the advantages of category theory is to enable one to prove many general results with a minimum of assumptions. Many common notions from mathematics (e.g. surjective, injective, free object
, basis
, finite representation
, isomorphism
) are definable purely in category theoretic terms (cf. monomorphism
, epimorphism
).
Category theory has been suggested as a foundation for mathematics on par with set theory
and type theory
(cf. topos
).
Allegory theory
provides a generalization comparable to category theory for relations
instead of functions.
Relative to set theorySet theorySet theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
These properties concern the domainDomain (mathematics)
In mathematics, the domain of definition or simply the domain of a function is the set of "input" or argument values for which the function is defined...
, the codomain
Codomain
In mathematics, the codomain or target set of a function is the set into which all of the output of the function is constrained to fall. It is the set in the notation...
and the range
Range (mathematics)
In mathematics, the range of a function refers to either the codomain or the image of the function, depending upon usage. This ambiguity is illustrated by the function f that maps real numbers to real numbers with f = x^2. Some books say that range of this function is its codomain, the set of all...
of functions.
- Injective functionInjective functionIn mathematics, an injective function is a function that preserves distinctness: it never maps distinct elements of its domain to the same element of its codomain. In other words, every element of the function's codomain is mapped to by at most one element of its domain...
: has a distinct value for each distinct argument. Also called an injection or, sometimes, one-to-one function. - Surjective functionSurjective functionIn mathematics, a function f from a set X to a set Y is surjective , or a surjection, if every element y in Y has a corresponding element x in X so that f = y...
: has a preimage for every element of the codomainCodomainIn mathematics, the codomain or target set of a function is the set into which all of the output of the function is constrained to fall. It is the set in the notation...
, i.e. the codomain equals the range. Also called a surjection or onto function. - Bijective function: is both an injectionInjective functionIn mathematics, an injective function is a function that preserves distinctness: it never maps distinct elements of its domain to the same element of its codomain. In other words, every element of the function's codomain is mapped to by at most one element of its domain...
and a surjection, and thus invertibleInverse functionIn mathematics, an inverse function is a function that undoes another function: If an input x into the function ƒ produces an output y, then putting y into the inverse function g produces the output x, and vice versa. i.e., ƒ=y, and g=x...
.
- Identity functionIdentity functionIn mathematics, an identity function, also called identity map or identity transformation, is a function that always returns the same value that was used as its argument...
: maps any given element to itself. - Constant functionConstant functionIn mathematics, a constant function is a function whose values do not vary and thus are constant. For example the function f = 4 is constant since f maps any value to 4...
: has a fixed value regardless of arguments. - Empty functionEmpty functionIn mathematics, an empty function is a function whose domain is the empty set. For each set A, there is exactly one such empty functionf_A: \varnothing \rightarrow A....
: whose domain equals the empty setEmpty setIn mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
.
Relative to an operator (c.q. a groupGroup theoryIn mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
or other structureMathematical structureIn mathematics, a structure on a set, or more generally a type, consists of additional mathematical objects that in some manner attach to the set, making it easier to visualize or work with, or endowing the collection with meaning or significance....
)
These properties concern how the function is affected by arithmeticArithmetic
Arithmetic or arithmetics is the oldest and most elementary branch of mathematics, used by almost everyone, for tasks ranging from simple day-to-day counting to advanced science and business calculations. It involves the study of quantity, especially as the result of combining numbers...
operations on its operand.
The following are special examples of a homomorphism
Homomorphism
In abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
on a binary operation
Binary operation
In mathematics, a binary operation is a calculation involving two operands, in other words, an operation whose arity is two. Examples include the familiar arithmetic operations of addition, subtraction, multiplication and division....
:
- Additive functionAdditive functionIn mathematics the term additive function has two different definitions, depending on the specific field of application.In algebra an additive function is a function that preserves the addition operation:for any two elements x and y in the domain. For example, any linear map is additive...
: preserves the addition operation: f(x+y) = f(x)+f(y). - Multiplicative functionMultiplicative functionIn number theory, a multiplicative function is an arithmetic function f of the positive integer n with the property that f = 1 and whenevera and b are coprime, then...
: preserves the multiplication operation: f(xy) = f(x)f(y).
Relative to negation
Negation
In logic and mathematics, negation, also called logical complement, is an operation on propositions, truth values, or semantic values more generally. Intuitively, the negation of a proposition is true when that proposition is false, and vice versa. In classical logic negation is normally identified...
:
- Even function: is symmetric with respect to the Y-axis. Formally, for each x: f(x) = f(−x).
- Odd function: is symmetric with respect to the originOrigin (mathematics)In mathematics, the origin of a Euclidean space is a special point, usually denoted by the letter O, used as a fixed point of reference for the geometry of the surrounding space. In a Cartesian coordinate system, the origin is the point where the axes of the system intersect...
. Formally, for each x: f(−x) = −f(x).
Relative to a binary operation and an order
Order theory
Order theory is a branch of mathematics which investigates our intuitive notion of order using binary relations. It provides a formal framework for describing statements such as "this is less than that" or "this precedes that". This article introduces the field and gives some basic definitions...
:
- Subadditive functionSubadditive functionIn mathematics, subadditivity is a property of a function that states, roughly, that evaluating the function for the sum of two elements of the domain always returns something less than or equal to the sum of the function's values at each element. There are numerous examples of subadditive...
: for which the value of f(x+y) is less than or equal to f(x)+f(y). - Superadditive function: for which the value of f(x+y) is greater than or equal to f(x)+f(y).
Relative to a topology
- Continuous functionContinuous functionIn mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
: in which preimages of open setOpen setThe concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
s are open. - Nowhere continuousNowhere continuousIn mathematics, a nowhere continuous function, also called an everywhere discontinuous function, is a function that is not continuous at any point of its domain...
function: is not continuous at any point of its domain (e.g. Dirichlet function). - HomeomorphismHomeomorphismIn the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
: is an injective functionInjective functionIn mathematics, an injective function is a function that preserves distinctness: it never maps distinct elements of its domain to the same element of its codomain. In other words, every element of the function's codomain is mapped to by at most one element of its domain...
that is also continuousContinuous functionIn mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
, whose inverseInverse functionIn mathematics, an inverse function is a function that undoes another function: If an input x into the function ƒ produces an output y, then putting y into the inverse function g produces the output x, and vice versa. i.e., ƒ=y, and g=x...
is continuous.
Relative to an ordering
- Monotonic functionMonotonic functionIn mathematics, a monotonic function is a function that preserves the given order. This concept first arose in calculus, and was later generalized to the more abstract setting of order theory....
: does not reverse ordering of any pair. - Strict Monotonic functionMonotonic functionIn mathematics, a monotonic function is a function that preserves the given order. This concept first arose in calculus, and was later generalized to the more abstract setting of order theory....
: preserves the given order.
Relative to the real/complex numbers
- Analytic functionAnalytic functionIn mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
: Can be defined locally by a convergent power series. - Arithmetic functionArithmetic functionIn number theory, an arithmetic function is a real or complex valued function ƒ defined on the set of natural numbers In number theory, an arithmetic (or arithmetical) function is a real or complex valued function ƒ(n) defined on the set of natural numbers In number theory, an arithmetic (or...
: A function from the positive integers into the complex numberComplex numberA complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s. - Differentiable functionDifferentiable functionIn calculus , a differentiable function is a function whose derivative exists at each point in its domain. The graph of a differentiable function must have a non-vertical tangent line at each point in its domain...
: Has a derivativeDerivativeIn calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
. - Smooth functionSmooth functionIn mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
: Has derivatives of all orders. - Holomorphic functionHolomorphic functionIn mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
: ComplexComplex numberA complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
valued function of a complex variable which is differentiable at every point in its domain. - Meromorphic functionMeromorphic functionIn complex analysis, a meromorphic function on an open subset D of the complex plane is a function that is holomorphic on all D except a set of isolated points, which are poles for the function...
: ComplexComplex numberA complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
valued function that is holomorphic everywhere, apart from at isolated points where there are poles. - Entire functionEntire functionIn complex analysis, an entire function, also called an integral function, is a complex-valued function that is holomorphic over the whole complex plane...
: A holomorphic functionHolomorphic functionIn mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
whose domain is the entire complex planeComplex numberA complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
.
Ways of defining functions/Relation to Type Theory
- Composite function: is formed by the composition of two functions f and g, by mapping x to f(g(x)).
- Inverse functionInverse functionIn mathematics, an inverse function is a function that undoes another function: If an input x into the function ƒ produces an output y, then putting y into the inverse function g produces the output x, and vice versa. i.e., ƒ=y, and g=x...
: is declared by "doing the reverse" of a given function (e.g. arcsine is the inverse of sineSineIn mathematics, the sine function is a function of an angle. In a right triangle, sine gives the ratio of the length of the side opposite to an angle to the length of the hypotenuse.Sine is usually listed first amongst the trigonometric functions....
). - Piecewise function: is defined by different expressions at different intervals.
In general, functions are often defined by specifying the name of a dependent variable, and a way of calculating what it should map to. For this purpose, the
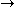 symbol or Church
symbol or ChurchAlonzo Church
Alonzo Church was an American mathematician and logician who made major contributions to mathematical logic and the foundations of theoretical computer science. He is best known for the lambda calculus, Church–Turing thesis, Frege–Church ontology, and the Church–Rosser theorem.-Life:Alonzo Church...
's
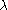
Lambda calculus
In mathematical logic and computer science, lambda calculus, also written as λ-calculus, is a formal system for function definition, function application and recursion. The portion of lambda calculus relevant to computation is now called the untyped lambda calculus...
is often used. Also, sometimes mathematicians notate a function's domain
Domain
-General:*Territory , a non-sovereign geographic area which has come under the authority of another government*Public domain, a body of works and knowledge without proprietary interest...
and codomain
Codomain
In mathematics, the codomain or target set of a function is the set into which all of the output of the function is constrained to fall. It is the set in the notation...
by writing e.g.
 . These notions extend directly to lambda calculus
. These notions extend directly to lambda calculusLambda calculus
In mathematical logic and computer science, lambda calculus, also written as λ-calculus, is a formal system for function definition, function application and recursion. The portion of lambda calculus relevant to computation is now called the untyped lambda calculus...
and type theory
Type theory
In mathematics, logic and computer science, type theory is any of several formal systems that can serve as alternatives to naive set theory, or the study of such formalisms in general...
, respectively.
Relation to Category Theory
Category TheoryCategory theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
is a branch of mathematics that formalizes the notion of a special function via arrows or morphisms. A category
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
is an algebraic object that (abstractly) consists of a class of objects, and for every pair of objects, a set of morphisms. A partial (equiv. dependently typed) binary operation called composition
Composition
Composition may refer to:* Composition , in which one assumes that a whole has a property solely because its various parts have that property* Compounding is also known as composition in linguistic literature* in computer science...
is provided on morphisms, every object has one special morphism from it to itself called the identity
Identity (mathematics)
In mathematics, the term identity has several different important meanings:*An identity is a relation which is tautologically true. This means that whatever the number or value may be, the answer stays the same. For example, algebraically, this occurs if an equation is satisfied for all values of...
on that object, and composition and identities are required to obey certain relations.
In a so-called concrete category
Concrete category
In mathematics, a concrete category is a category that is equipped with a faithful functor to the category of sets. This functor makes it possible to think of the objects of the category as sets with additional structure, and of its morphisms as structure-preserving functions...
, the objects are associated with mathematical structures like sets, magmas, groups
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
, rings
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
, topological spaces, vector spaces, metric spaces, partial orders
Order theory
Order theory is a branch of mathematics which investigates our intuitive notion of order using binary relations. It provides a formal framework for describing statements such as "this is less than that" or "this precedes that". This article introduces the field and gives some basic definitions...
, differentiable manifolds, uniform spaces, etc., and morphisms between two objects are associated with structure-preserving functions between them. In the examples above, these would be functions
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
, magma homomorphisms, group homomorphisms, ring homomorphisms, continuous functions, linear transformations (or matrices
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
), metric maps, monotonic function
Monotonic function
In mathematics, a monotonic function is a function that preserves the given order. This concept first arose in calculus, and was later generalized to the more abstract setting of order theory....
s, differentiable functions, and uniformly continuous functions, respectively.
As an algebraic theory, one of the advantages of category theory is to enable one to prove many general results with a minimum of assumptions. Many common notions from mathematics (e.g. surjective, injective, free object
Free object
In mathematics, the idea of a free object is one of the basic concepts of abstract algebra. It is a part of universal algebra, in the sense that it relates to all types of algebraic structure . It also has a formulation in terms of category theory, although this is in yet more abstract terms....
, basis
Basis
Basis may refer to* Cost basis, in income tax law, the original cost of property adjusted for factors such as depreciation.* Basis of futures, the value differential between a future and the spot price...
, finite representation
Representation
Representation can refer to:* Representation , one's ability to influence the political process* Representative democracy* Representation, a type of diplomatic mission...
, isomorphism
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
) are definable purely in category theoretic terms (cf. monomorphism
Monomorphism
In the context of abstract algebra or universal algebra, a monomorphism is an injective homomorphism. A monomorphism from X to Y is often denoted with the notation X \hookrightarrow Y....
, epimorphism
Epimorphism
In category theory, an epimorphism is a morphism f : X → Y which is right-cancellative in the sense that, for all morphisms ,...
).
Category theory has been suggested as a foundation for mathematics on par with set theory
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
and type theory
Type theory
In mathematics, logic and computer science, type theory is any of several formal systems that can serve as alternatives to naive set theory, or the study of such formalisms in general...
(cf. topos
Topos
In mathematics, a topos is a type of category that behaves like the category of sheaves of sets on a topological space...
).
Allegory theory
Allegory (category theory)
In mathematical category theory, an allegory is a category that has some of the structure of the category of sets and binary relations between them. Allegories can be used as an abstraction of categories of relations, and in this sense the theory of allegories is a generalization of relation...
provides a generalization comparable to category theory for relations
Relation (mathematics)
In set theory and logic, a relation is a property that assigns truth values to k-tuples of individuals. Typically, the property describes a possible connection between the components of a k-tuple...
instead of functions.

