Transcendental function
Encyclopedia
A transcendental function is a function
that does not satisfy a polynomial
equation whose coefficient
s are themselves polynomials, in contrast to an algebraic function
, which does satisfy such an equation. In other words, a transcendental function is a function that "transcends" algebra
in the sense that it cannot be expressed in terms of a finite sequence of the algebraic operations of addition, multiplication, and root extraction.
Examples of transcendental functions include the exponential function
, the logarithm
, and the trigonometric function
s.
Formally, an analytic function
ƒ(z) of the real or complex variables z1,…,zn is transcendental if the n + 1 functions z1,…,zn, ƒ(z) are algebraically independent
. That is, ƒ is transcendental
over the field C(z1,…,zn).
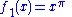
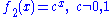
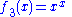
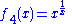
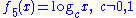
Note that in particular for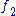
if we set c equal to 
, the base of the natural logarithm
, then we get that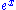
is a transcendental function. Similarly, if we set c equal to 
in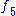 
, then we get that 
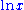, the natural logarithm
, is a transcendental function.
and the exponential function
are examples of transcendental functions. Transcendental function is a term often used to describe the trigonometric function
s (sine
, cosine, tangent, their reciprocals cotangent, secant, and cosecant, the now little-used versine, haversine
, and coversine]], their analogs the hyperbolic functions and so forth).
A function that is not transcendental is said to be algebraic. Examples of algebraic functions are rational functions and the square root
function.
The operation of taking the indefinite integral of an algebraic function is a source of transcendental functions. For example, the logarithm function arose from the reciprocal function
in an effort to find the area of a hyperbolic sector. Thus the hyperbolic angle
and the hyperbolic function
s sinh, cosh, and tanh are all transcendental.
Differential algebra
examines how integration frequently creates functions that are algebraically independent of some class, such as when one takes polynomials with trigonometric functions as variables.
, transcendental functions are notable because they make sense only when their argument is dimensionless (possibly after algebraic reduction). Because of this, transcendental functions can be an easy-to-spot source of dimensional errors. For example, log(10 m) is a nonsensical expression, unlike log(5 meters / 3 meters) or log(3) meters . One could attempt to apply a logarithm
ic identity to get log(10) + log(m), which highlights the problem: applying a non-algebraic operation to a dimension creates meaningless results.
then ƒ(α) will also be an algebraic number. The converse is not true: there are entire transcendental functions ƒ(z) such that ƒ(α) is an algebraic number for any algebraic α. In many instances, however, the set of algebraic numbers α where ƒ(α) is algebraic is fairly small. For example, if ƒ is the exponential function, ƒ(z) = ez, then the only algebraic number α where ƒ(α) is also algebraic is α = 0, where ƒ(α) = 1. For a given transcendental function this set of algebraic numbers giving algebraic results is called the exceptional set of the function, that is the set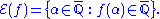
If this set can be calculated then it can often lead to results in transcendence theory
. For example, Lindemann
proved in 1882 that the exceptional set of the exponential function is just {0}. In particular exp(1) = e is transcendental. Also, since exp(iπ) = −1 is algebraic we know that iπ cannot be algebraic. Since i is algebraic this implies that π is a transcendental number
.
In general, finding the exceptional set of a function is a difficult problem, but it has been calculated for some functions:
While calculating the exceptional set for a given function is not easy, it is known that given any subset of the algebraic numbers, say A, there is a transcendental function ƒ whose exceptional set is A. Since, as mentioned above, this includes taking A to be the whole set of algebraic numbers, there is no way to determine if a function is transcendental just by looking at its values at algebraic numbers. In fact, Alex Wilkie
showed that the situation is even worse: he constructed a transcendental function ƒ from R to R that is analytic everywhere but whose transcendence cannot be detected by any first-order
method.
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
that does not satisfy a polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
equation whose coefficient
Coefficient
In mathematics, a coefficient is a multiplicative factor in some term of an expression ; it is usually a number, but in any case does not involve any variables of the expression...
s are themselves polynomials, in contrast to an algebraic function
Algebraic function
In mathematics, an algebraic function is informally a function that satisfies a polynomial equation whose coefficients are themselves polynomials with rational coefficients. For example, an algebraic function in one variable x is a solution y for an equationwhere the coefficients ai are polynomial...
, which does satisfy such an equation. In other words, a transcendental function is a function that "transcends" algebra
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
in the sense that it cannot be expressed in terms of a finite sequence of the algebraic operations of addition, multiplication, and root extraction.
Examples of transcendental functions include the exponential function
Exponential function
In mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
, the logarithm
Logarithm
The logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
, and the trigonometric function
Trigonometric function
In mathematics, the trigonometric functions are functions of an angle. They are used to relate the angles of a triangle to the lengths of the sides of a triangle...
s.
Formally, an analytic function
Analytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
ƒ(z) of the real or complex variables z1,…,zn is transcendental if the n + 1 functions z1,…,zn, ƒ(z) are algebraically independent
Algebraic independence
In abstract algebra, a subset S of a field L is algebraically independent over a subfield K if the elements of S do not satisfy any non-trivial polynomial equation with coefficients in K...
. That is, ƒ is transcendental
Algebraic element
In mathematics, if L is a field extension of K, then an element a of L is called an algebraic element over K, or just algebraic over K, if there exists some non-zero polynomial g with coefficients in K such that g=0...
over the field C(z1,…,zn).
Some examples
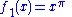
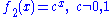
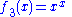
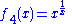
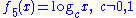
All of the following functions are transcendental.Note that in particular for
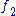if we set c equal to , the base of the natural logarithmExponential function
In mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
, then we get that
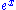is a transcendental function. Similarly, if we set c equal to in 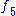, then we get that 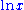, the natural logarithmNatural logarithm
The natural logarithm is the logarithm to the base e, where e is an irrational and transcendental constant approximately equal to 2.718281828...
, is a transcendental function.
Algebraic and transcendental functions
The logarithmLogarithm
The logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
and the exponential function
Exponential function
In mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
are examples of transcendental functions. Transcendental function is a term often used to describe the trigonometric function
Trigonometric function
In mathematics, the trigonometric functions are functions of an angle. They are used to relate the angles of a triangle to the lengths of the sides of a triangle...
s (sine
Sine
In mathematics, the sine function is a function of an angle. In a right triangle, sine gives the ratio of the length of the side opposite to an angle to the length of the hypotenuse.Sine is usually listed first amongst the trigonometric functions....
, cosine, tangent, their reciprocals cotangent, secant, and cosecant, the now little-used versine, haversine
Versine
The versine or versed sine, versin, is a trigonometric function equal to and 2sin2. It appeared in some of the earliest trigonometric tables and was once widespread, but it is now little-used...
, and coversine]], their analogs the hyperbolic functions and so forth).
A function that is not transcendental is said to be algebraic. Examples of algebraic functions are rational functions and the square root
Square root
In mathematics, a square root of a number x is a number r such that r2 = x, or, in other words, a number r whose square is x...
function.
The operation of taking the indefinite integral of an algebraic function is a source of transcendental functions. For example, the logarithm function arose from the reciprocal function
Multiplicative inverse
In mathematics, a multiplicative inverse or reciprocal for a number x, denoted by 1/x or x−1, is a number which when multiplied by x yields the multiplicative identity, 1. The multiplicative inverse of a fraction a/b is b/a. For the multiplicative inverse of a real number, divide 1 by the...
in an effort to find the area of a hyperbolic sector. Thus the hyperbolic angle
Hyperbolic angle
In mathematics, a hyperbolic angle is a geometric figure that divides a hyperbola. The science of hyperbolic angle parallels the relation of an ordinary angle to a circle...
and the hyperbolic function
Hyperbolic function
In mathematics, hyperbolic functions are analogs of the ordinary trigonometric, or circular, functions. The basic hyperbolic functions are the hyperbolic sine "sinh" , and the hyperbolic cosine "cosh" , from which are derived the hyperbolic tangent "tanh" and so on.Just as the points form a...
s sinh, cosh, and tanh are all transcendental.
Differential algebra
Differential algebra
In mathematics, differential rings, differential fields, and differential algebras are rings, fields, and algebras equipped with a derivation, which is a unary function that is linear and satisfies the Leibniz product law...
examines how integration frequently creates functions that are algebraically independent of some class, such as when one takes polynomials with trigonometric functions as variables.
Dimensional analysis
In dimensional analysisDimensional analysis
In physics and all science, dimensional analysis is a tool to find or check relations among physical quantities by using their dimensions. The dimension of a physical quantity is the combination of the basic physical dimensions which describe it; for example, speed has the dimension length per...
, transcendental functions are notable because they make sense only when their argument is dimensionless (possibly after algebraic reduction). Because of this, transcendental functions can be an easy-to-spot source of dimensional errors. For example, log(10 m) is a nonsensical expression, unlike log(5 meters / 3 meters) or log(3) meters . One could attempt to apply a logarithm
Logarithm
The logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
ic identity to get log(10) + log(m), which highlights the problem: applying a non-algebraic operation to a dimension creates meaningless results.
Exceptional set
If ƒ(z) is an algebraic function and α is an algebraic numberAlgebraic number
In mathematics, an algebraic number is a number that is a root of a non-zero polynomial in one variable with rational coefficients. Numbers such as π that are not algebraic are said to be transcendental; almost all real numbers are transcendental...
then ƒ(α) will also be an algebraic number. The converse is not true: there are entire transcendental functions ƒ(z) such that ƒ(α) is an algebraic number for any algebraic α. In many instances, however, the set of algebraic numbers α where ƒ(α) is algebraic is fairly small. For example, if ƒ is the exponential function, ƒ(z) = ez, then the only algebraic number α where ƒ(α) is also algebraic is α = 0, where ƒ(α) = 1. For a given transcendental function this set of algebraic numbers giving algebraic results is called the exceptional set of the function, that is the set
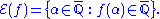
If this set can be calculated then it can often lead to results in transcendence theory
Transcendence theory
Transcendence theory is a branch of number theory that investigates transcendental numbers, in both qualitative and quantitative ways.-Transcendence:...
. For example, Lindemann
Ferdinand von Lindemann
Carl Louis Ferdinand von Lindemann was a German mathematician, noted for his proof, published in 1882, that π is a transcendental number, i.e., it is not a root of any polynomial with rational coefficients....
proved in 1882 that the exceptional set of the exponential function is just {0}. In particular exp(1) = e is transcendental. Also, since exp(iπ) = −1 is algebraic we know that iπ cannot be algebraic. Since i is algebraic this implies that π is a transcendental number
Transcendental number
In mathematics, a transcendental number is a number that is not algebraic—that is, it is not a root of a non-constant polynomial equation with rational coefficients. The most prominent examples of transcendental numbers are π and e...
.
In general, finding the exceptional set of a function is a difficult problem, but it has been calculated for some functions:
,
,
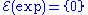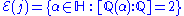- Here j is Klein's j-invariantJ-invariantIn mathematics, Klein's j-invariant, regarded as a function of a complex variable τ, is a modular function defined on the upper half-plane of complex numbers.We haveThe modular discriminant \Delta is defined as \Delta=g_2^3-27g_3^2...
, H is the upper half-plane, and [Q(α):Q] is the degreeDegree of a field extensionIn mathematics, more specifically field theory, the degree of a field extension is a rough measure of the "size" of the extension. The concept plays an important role in many parts of mathematics, including algebra and number theory — indeed in any area where fields appear prominently.-...
of the number fieldAlgebraic number fieldIn mathematics, an algebraic number field F is a finite field extension of the field of rational numbers Q...
Q(α). This result is due to Theodor SchneiderTheodor SchneiderTheodor Schneider was a German mathematician, best known for providing proof of what is now known as the Gelfond–Schneider theorem in 1935....
.
- Here j is Klein's j-invariant
,
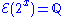- This result is a corollary of the Gelfond–Schneider theorem which says that if α is algebraic and not 0 or 1, and if β is algebraic and irrational then αβ is transcendental. Thus the function 2x could be replaced by cx for any algebraic c not equal to 0 or 1. Indeed, we have:
- A consequence of Schanuel's conjectureSchanuel's conjectureIn mathematics, specifically transcendence theory, Schanuel's conjecture is a conjecture made by Stephen Schanuel in the 1960s concerning the transcendence degree of certain field extensions of the rational numbers.-Statement:The conjecture is as follows:...
in transcendental number theoryTranscendence theoryTranscendence theory is a branch of number theory that investigates transcendental numbers, in both qualitative and quantitative ways.-Transcendence:...
would be that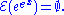
- A function with empty exceptional set that doesn't require one to assume this conjecture is the function ƒ(x) = exp(1 + πx).
While calculating the exceptional set for a given function is not easy, it is known that given any subset of the algebraic numbers, say A, there is a transcendental function ƒ whose exceptional set is A. Since, as mentioned above, this includes taking A to be the whole set of algebraic numbers, there is no way to determine if a function is transcendental just by looking at its values at algebraic numbers. In fact, Alex Wilkie
Alex Wilkie
Alex Wilkie FRS is a British mathematician known for his contributions to Model theory and logic. Previously Reader in Mathematical Logic at the University of Oxford, he was appointed to the Fielden Chair of Pure Mathematics at the University of Manchester in 2007.Wilkie attended Aylesbury...
showed that the situation is even worse: he constructed a transcendental function ƒ from R to R that is analytic everywhere but whose transcendence cannot be detected by any first-order
First-order logic
First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
method.
See also
- Algebraic functionAlgebraic functionIn mathematics, an algebraic function is informally a function that satisfies a polynomial equation whose coefficients are themselves polynomials with rational coefficients. For example, an algebraic function in one variable x is a solution y for an equationwhere the coefficients ai are polynomial...
- Analytic functionAnalytic functionIn mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
- Complex function
- Generalized functions
- Special function