Riesz function
Encyclopedia
In mathematics
, the Riesz function is an entire function
defined by Marcel Riesz
in connection with the Riemann hypothesis
, by means of the power series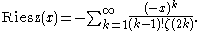
If we set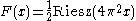
we may define it in terms of the coefficients of the Laurent series development of the hyperbolic (or equivalently, the ordinary) cotangent around zero. If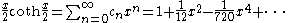
then F may be defined as
The values of ζ(2k) approach one for increasing k, and comparing the series for the Riesz function with that for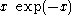
shows that it defines an entire function. Alternatively, F may be defined as
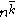denotes the rising factorial power in the notation of D. E. Knuth and the number Bn are the Bernoulli number
. The series is one of alternating terms and the function quickly tends to minus infinity for increasingly negative values of x. Positive values of x are more interesting and delicate.
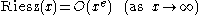
for any exponent e larger than 1/2, where this is big O notation
; taking values both positive and negative. Riesz showed that the Riemann hypothesis is equivalent to the claim that the above is true for any e larger than 1/4. In the same paper, he added a slightly pessimistic note too: «Je ne sais pas encore decider si cette condition facilitera la vérification de l'hypothèse».
. If we take
we see that if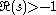
then
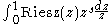
converges, whereas from the growth condition we have that if
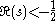then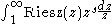
converges. Putting this together, we see the Mellin transform of the Riesz function is defined on the strip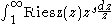
.
On this strip, we have
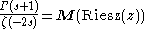
From the inverse Mellin transform, we now get an expression for the Riesz function, as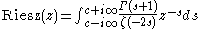
where c is between minus one and minus one-half. If the Riemann hypothesis is true, we can move the line of integration to any value less than minus one-fourth, and hence we get the equivalence between the fourth-root rate of growth for the Riesz function and the Riemann hypothesis.
G. H. Hardy
gave the integral representation of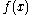
using Borel resummation as
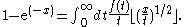
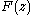for 
. However, this would require evaluating a polynomial of degree 1000 either using rational arithmetic with the coefficients of large numerator or denominator, or using floating point computations of over 100 digits. An alternative is to use the inverse Mellin transform defined above and numerically integrate. Neither approach is computationally easy.
Another approach is to use acceleration of convergence. We have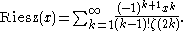
Since ζ(2k) approaches one as k grows larger, the terms of this series approach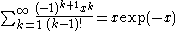
. Indeed, Riesz noted that: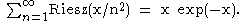 
Using Kummer's method for accelerating convergence gives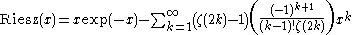
with an improved rate of convergence.
Continuing this process leads to a new series for the Riesz function with much better convergence properties: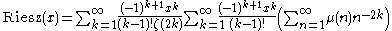
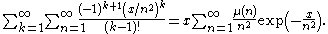
Here μ is the Möbius mu function, and the rearrangement of terms is justified by absolute convergence. We may now apply Kummer's method again, and write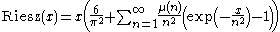
the terms of which eventually decrease as the inverse fourth power of n.
The above series are absolutely convergent everywhere, and hence may be differentiated term by term, leading to the following expression for the derivative of the Riesz function: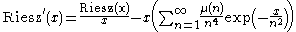
which may be rearranged as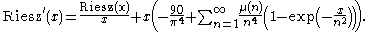
Marek Wolf in
assuming the Riemann Hypthesis has shown that for large x: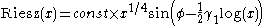
where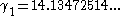
is the imaginary part
of the first nontrivial zero of the zeta function,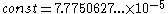
and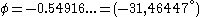 
. It agrees with the general theorems
about zeros of the Riesz function proved in 1964 by Herbert Wilf.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Riesz function is an entire function
Entire function
In complex analysis, an entire function, also called an integral function, is a complex-valued function that is holomorphic over the whole complex plane...
defined by Marcel Riesz
Marcel Riesz
Marcel Riesz was a Hungarian mathematician who was born in Győr, Hungary . He moved to Sweden in 1908 and spent the rest of his life there, dying in Lund, where he was a professor from 1926 at Lund University...
in connection with the Riemann hypothesis
Riemann hypothesis
In mathematics, the Riemann hypothesis, proposed by , is a conjecture about the location of the zeros of the Riemann zeta function which states that all non-trivial zeros have real part 1/2...
, by means of the power series
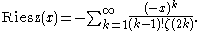
If we set
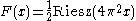we may define it in terms of the coefficients of the Laurent series development of the hyperbolic (or equivalently, the ordinary) cotangent around zero. If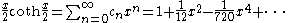then F may be defined as
The values of ζ(2k) approach one for increasing k, and comparing the series for the Riesz function with that for
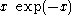shows that it defines an entire function. Alternatively, F may be defined as 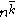denotes the rising factorial power in the notation of D. E. Knuth and the number Bn are the Bernoulli numberBernoulli number
In mathematics, the Bernoulli numbers Bn are a sequence of rational numbers with deep connections to number theory. They are closely related to the values of the Riemann zeta function at negative integers....
. The series is one of alternating terms and the function quickly tends to minus infinity for increasingly negative values of x. Positive values of x are more interesting and delicate.
Riesz criterion
It can be shown that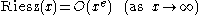for any exponent e larger than 1/2, where this is big O notation
Big O notation
In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
; taking values both positive and negative. Riesz showed that the Riemann hypothesis is equivalent to the claim that the above is true for any e larger than 1/4. In the same paper, he added a slightly pessimistic note too: «Je ne sais pas encore decider si cette condition facilitera la vérification de l'hypothèse».
Mellin transform of the Riesz function
The Riesz function is related to the Riemann zeta function via its Mellin transformMellin transform
In mathematics, the Mellin transform is an integral transform that may be regarded as the multiplicative version of the two-sided Laplace transform...
. If we take
we see that if
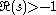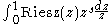
thenconverges, whereas from the growth condition we have that if
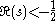then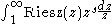converges. Putting this together, we see the Mellin transform of the Riesz function is defined on the strip
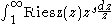.On this strip, we have
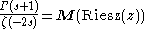
From the inverse Mellin transform, we now get an expression for the Riesz function, as
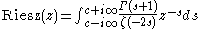
where c is between minus one and minus one-half. If the Riemann hypothesis is true, we can move the line of integration to any value less than minus one-fourth, and hence we get the equivalence between the fourth-root rate of growth for the Riesz function and the Riemann hypothesis.
G. H. Hardy
G. H. Hardy
Godfrey Harold “G. H.” Hardy FRS was a prominent English mathematician, known for his achievements in number theory and mathematical analysis....
gave the integral representation of
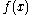using Borel resummation as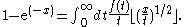Calculation of the Riesz function
The Maclaurin series coefficients of F increase in absolute value until they reach their maximum at the 40th term of -1.753. By the 109th term they have dropped below one in absolute value. Taking the first 1000 terms suffices to give a very accurate value for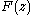 for . However, this would require evaluating a polynomial of degree 1000 either using rational arithmetic with the coefficients of large numerator or denominator, or using floating point computations of over 100 digits. An alternative is to use the inverse Mellin transform defined above and numerically integrate. Neither approach is computationally easy.Another approach is to use acceleration of convergence. We have
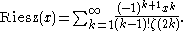
Since ζ(2k) approaches one as k grows larger, the terms of this series approach
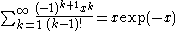. Indeed, Riesz noted that: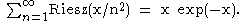 Using Kummer's method for accelerating convergence gives
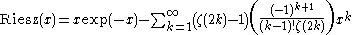
with an improved rate of convergence.
Continuing this process leads to a new series for the Riesz function with much better convergence properties:
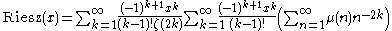
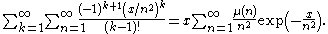
Here μ is the Möbius mu function, and the rearrangement of terms is justified by absolute convergence. We may now apply Kummer's method again, and write
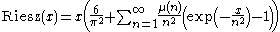
the terms of which eventually decrease as the inverse fourth power of n.
The above series are absolutely convergent everywhere, and hence may be differentiated term by term, leading to the following expression for the derivative of the Riesz function:
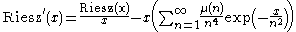
which may be rearranged as
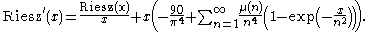
Marek Wolf in
assuming the Riemann Hypthesis has shown that for large x:
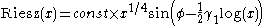
where
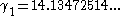is the imaginary partof the first nontrivial zero of the zeta function,
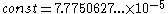and 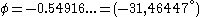. It agrees with the general theoremsabout zeros of the Riesz function proved in 1964 by Herbert Wilf.