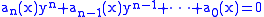
Algebraic function
Encyclopedia
In mathematics
, an algebraic function is informally a function
that satisfies a polynomial
equation whose coefficient
s are themselves polynomials with rational coefficients. For example, an algebraic function in one variable x is a solution y for an equation
where the coefficients ai(x) are polynomial functions of x with rational coefficients. A function which is not algebraic is called a transcendental function
.
In more precise terms, an algebraic function may not be a function at all, at least not in the conventional sense. Consider for example the equation of a circle
:
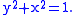
This determines y, except only up to
an overall sign:
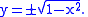
However, both branches are thought of as belonging to the "function" determined by the polynomial equation. Thus an algebraic function is most naturally considered as a multiple valued function.
An algebraic function in n variables is similarly defined as a function y which solves a polynomial equation in n + 1 variables:
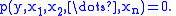
It is normally assumed that p should be an irreducible polynomial
. The existence of an algebraic function is then guaranteed by the implicit function theorem
.
Formally, an algebraic function in n variables over the field
K is an element of the algebraic closure
of the field of rational function
s K(x1,...,xn). In order to understand algebraic functions as functions, it becomes necessary to introduce ideas relating to Riemann surface
s or more generally algebraic varieties, and sheaf theory
.
, multiplication
, division
, and taking an nth root
. Of course, this is something of an oversimplification; because of casus irreducibilis
(and more generally the fundamental theorem of Galois theory
), algebraic functions need not be expressible by radicals.
First, note that any polynomial is an algebraic function, since polynomials are simply the solutions for y of the equation
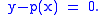
More generally, any rational function is algebraic, being the solution of

Moreover, the nth root of any polynomial is an algebraic function, solving the equation

Surprisingly, the inverse function
of an algebraic function is an algebraic function. For supposing that y is a solution of
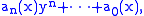
for each value of x, then x is also a solution of this equation for each value of y. Indeed, interchanging the roles of x and y and gathering terms,
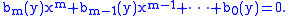
Writing x as a function of y gives the inverse function, also an algebraic function.
However, not every function has an inverse. For example, y = x2 fails the horizontal line test
: it fails to be one-to-one. The inverse is the algebraic "function" . In this sense, algebraic functions are often not true functions at all, but instead are multiple valued functions.
. In this sense, algebraic functions are often not true functions at all, but instead are multiple valued functions.
Another way to understand this, which will become important later in the article, is that an algebraic function is the graph of an algebraic curve
.
, the complex numbers are an algebraically closed field
. Hence any polynomial relation
is guaranteed to have at least one solution (and in general a number of solutions not exceeding the degree of p in x) for y at each point x, provided we allow y to assume complex as well as real values. Thus, problems to do with the domain
of an algebraic function can safely be minimized.
 Furthermore, even if one is ultimately interested in real algebraic functions, there may be no adequate means to express the function in a simple manner without resorting to complex numbers (see casus irreducibilis
Furthermore, even if one is ultimately interested in real algebraic functions, there may be no adequate means to express the function in a simple manner without resorting to complex numbers (see casus irreducibilis
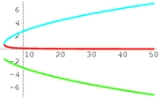
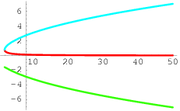
). For example, consider the algebraic function determined by the equation
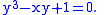
Using the cubic formula, one solution is (the red curve in the accompanying image)
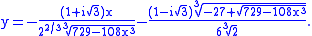
There is no way to express this function in terms of real numbers only, even though the resulting function is real-valued on the domain of the graph shown.
On a more significant theoretical level, using complex numbers allow one to use the powerful techniques of complex analysis
to discuss algebraic functions. In particular, the argument principle
can be used to show that any algebraic function is in fact an analytic function
, at least in the multiple-valued sense.
Formally, let p(x, y) be a complex polynomial in the complex variables x and y. Suppose that
x0 ∈ C is such that the polynomial p(x0,y) of y has n distinct zeros. We shall show that the algebraic function is analytic in a neighborhood of x0. Choose a system of n non-overlapping discs Δi containing each of these zeros. Then by the argument principle
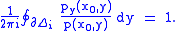
By continuity, this also holds for all x in a neighborhood of x0. In particular, p(x,y) has only one root in Δi, given by the residue theorem
:
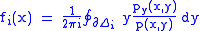
which is an analytic function.
vanishes. Hence there are only finitely many such points c1, ..., cm.
A close analysis of the properties of the function elements fi near the critical points can be used to show that the monodromy cover
is ramified
over the critical points (and possibly the point at infinity
). Thus the entire function
associated to the fi has at worst algebraic poles and ordinary algebraic branchings over the critical points.
Note that, away from the critical points, we have
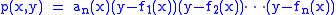
since the fi are by definition the distinct zeros of p. The monodromy group acts by permuting the factors, and thus forms the monodromy representation of the Galois group
of p. (The monodromy action on the universal covering space is related but different notion in the theory of Riemann surfaces.)
. The first discussion of algebraic functions appears to have been in Edward Waring
's 1794 An Essay on the Principles of Human Knowledge in which he writes:
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, an algebraic function is informally a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
that satisfies a polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
equation whose coefficient
Coefficient
In mathematics, a coefficient is a multiplicative factor in some term of an expression ; it is usually a number, but in any case does not involve any variables of the expression...
s are themselves polynomials with rational coefficients. For example, an algebraic function in one variable x is a solution y for an equation
where the coefficients ai(x) are polynomial functions of x with rational coefficients. A function which is not algebraic is called a transcendental function
Transcendental function
A transcendental function is a function that does not satisfy a polynomial equation whose coefficients are themselves polynomials, in contrast to an algebraic function, which does satisfy such an equation...
.
In more precise terms, an algebraic function may not be a function at all, at least not in the conventional sense. Consider for example the equation of a circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
:
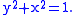
This determines y, except only up to
Up to
In mathematics, the phrase "up to x" means "disregarding a possible difference in x".For instance, when calculating an indefinite integral, one could say that the solution is f "up to addition by a constant," meaning it differs from f, if at all, only by some constant.It indicates that...
an overall sign:
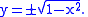
However, both branches are thought of as belonging to the "function" determined by the polynomial equation. Thus an algebraic function is most naturally considered as a multiple valued function.
An algebraic function in n variables is similarly defined as a function y which solves a polynomial equation in n + 1 variables:
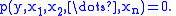
It is normally assumed that p should be an irreducible polynomial
Irreducible polynomial
In mathematics, the adjective irreducible means that an object cannot be expressed as the product of two or more non-trivial factors in a given set. See also factorization....
. The existence of an algebraic function is then guaranteed by the implicit function theorem
Implicit function theorem
In multivariable calculus, the implicit function theorem is a tool which allows relations to be converted to functions. It does this by representing the relation as the graph of a function. There may not be a single function whose graph is the entire relation, but there may be such a function on...
.
Formally, an algebraic function in n variables over the field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
K is an element of the algebraic closure
Algebraic closure
In mathematics, particularly abstract algebra, an algebraic closure of a field K is an algebraic extension of K that is algebraically closed. It is one of many closures in mathematics....
of the field of rational function
Rational function
In mathematics, a rational function is any function which can be written as the ratio of two polynomial functions. Neither the coefficients of the polynomials nor the values taken by the function are necessarily rational.-Definitions:...
s K(x1,...,xn). In order to understand algebraic functions as functions, it becomes necessary to introduce ideas relating to Riemann surface
Riemann surface
In mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...
s or more generally algebraic varieties, and sheaf theory
Sheaf (mathematics)
In mathematics, a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of...
.
Introduction and overview
The informal definition of an algebraic function provides a number of clues about the properties of algebraic functions. To gain an intuitive understanding, it may be helpful to regard algebraic functions as functions which can be formed by the usual algebraic operations: additionAddition
Addition is a mathematical operation that represents combining collections of objects together into a larger collection. It is signified by the plus sign . For example, in the picture on the right, there are 3 + 2 apples—meaning three apples and two other apples—which is the same as five apples....
, multiplication
Multiplication
Multiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
, division
Division (mathematics)
right|thumb|200px|20 \div 4=5In mathematics, especially in elementary arithmetic, division is an arithmetic operation.Specifically, if c times b equals a, written:c \times b = a\,...
, and taking an nth root
Nth root
In mathematics, the nth root of a number x is a number r which, when raised to the power of n, equals xr^n = x,where n is the degree of the root...
. Of course, this is something of an oversimplification; because of casus irreducibilis
Casus irreducibilis
In algebra, casus irreducibilis is one of the cases that may arise in attempting to solve a cubic equation with integer coefficients with roots that are expressed with radicals...
(and more generally the fundamental theorem of Galois theory
Fundamental theorem of Galois theory
In mathematics, the fundamental theorem of Galois theory is a result that describes the structure of certain types of field extensions.In its most basic form, the theorem asserts that given a field extension E /F which is finite and Galois, there is a one-to-one correspondence between its...
), algebraic functions need not be expressible by radicals.
First, note that any polynomial is an algebraic function, since polynomials are simply the solutions for y of the equation
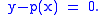
More generally, any rational function is algebraic, being the solution of

Moreover, the nth root of any polynomial is an algebraic function, solving the equation

Surprisingly, the inverse function
Inverse function
In mathematics, an inverse function is a function that undoes another function: If an input x into the function ƒ produces an output y, then putting y into the inverse function g produces the output x, and vice versa. i.e., ƒ=y, and g=x...
of an algebraic function is an algebraic function. For supposing that y is a solution of
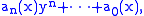
for each value of x, then x is also a solution of this equation for each value of y. Indeed, interchanging the roles of x and y and gathering terms,
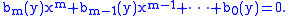
Writing x as a function of y gives the inverse function, also an algebraic function.
However, not every function has an inverse. For example, y = x2 fails the horizontal line test
Horizontal line test
In mathematics, the horizontal line test is a test used to determine if a function is injective and/or surjective.The lines used for the test are parallel to the x axis....
: it fails to be one-to-one. The inverse is the algebraic "function"
 . In this sense, algebraic functions are often not true functions at all, but instead are multiple valued functions.
. In this sense, algebraic functions are often not true functions at all, but instead are multiple valued functions.Another way to understand this, which will become important later in the article, is that an algebraic function is the graph of an algebraic curve
Algebraic curve
In algebraic geometry, an algebraic curve is an algebraic variety of dimension one. The theory of these curves in general was quite fully developed in the nineteenth century, after many particular examples had been considered, starting with circles and other conic sections.- Plane algebraic curves...
.
The role of complex numbers
From an algebraic perspective, complex numbers enter quite naturally into the study of algebraic functions. First of all, by the fundamental theorem of algebraFundamental theorem of algebra
The fundamental theorem of algebra states that every non-constant single-variable polynomial with complex coefficients has at least one complex root...
, the complex numbers are an algebraically closed field
Algebraically closed field
In mathematics, a field F is said to be algebraically closed if every polynomial with one variable of degree at least 1, with coefficients in F, has a root in F.-Examples:...
. Hence any polynomial relation
- p(y, x) = 0
is guaranteed to have at least one solution (and in general a number of solutions not exceeding the degree of p in x) for y at each point x, provided we allow y to assume complex as well as real values. Thus, problems to do with the domain
Domain (mathematics)
In mathematics, the domain of definition or simply the domain of a function is the set of "input" or argument values for which the function is defined...
of an algebraic function can safely be minimized.

Casus irreducibilis
In algebra, casus irreducibilis is one of the cases that may arise in attempting to solve a cubic equation with integer coefficients with roots that are expressed with radicals...
). For example, consider the algebraic function determined by the equation
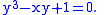
Using the cubic formula, one solution is (the red curve in the accompanying image)
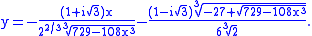
There is no way to express this function in terms of real numbers only, even though the resulting function is real-valued on the domain of the graph shown.
On a more significant theoretical level, using complex numbers allow one to use the powerful techniques of complex analysis
Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
to discuss algebraic functions. In particular, the argument principle
Argument principle
In complex analysis, the argument principle determines the difference between the number of zeros and poles of a meromorphic function by computing a contour integral of the function's logarithmic derivative....
can be used to show that any algebraic function is in fact an analytic function
Analytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
, at least in the multiple-valued sense.
Formally, let p(x, y) be a complex polynomial in the complex variables x and y. Suppose that
x0 ∈ C is such that the polynomial p(x0,y) of y has n distinct zeros. We shall show that the algebraic function is analytic in a neighborhood of x0. Choose a system of n non-overlapping discs Δi containing each of these zeros. Then by the argument principle
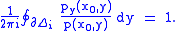
By continuity, this also holds for all x in a neighborhood of x0. In particular, p(x,y) has only one root in Δi, given by the residue theorem
Residue theorem
The residue theorem, sometimes called Cauchy's Residue Theorem, in complex analysis is a powerful tool to evaluate line integrals of analytic functions over closed curves and can often be used to compute real integrals as well. It generalizes the Cauchy integral theorem and Cauchy's integral formula...
:
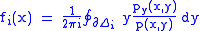
which is an analytic function.
Monodromy
Note that the foregoing proof of analyticity derived an expression for a system of n different function elements fi(x), provided that x is not a critical point of p(x, y). A critical point is a point where the number of distinct zeros is smaller than the degree of p, and this occurs only where the highest degree term of p vanishes, and where the discriminantDiscriminant
In algebra, the discriminant of a polynomial is an expression which gives information about the nature of the polynomial's roots. For example, the discriminant of the quadratic polynomialax^2+bx+c\,is\Delta = \,b^2-4ac....
vanishes. Hence there are only finitely many such points c1, ..., cm.
A close analysis of the properties of the function elements fi near the critical points can be used to show that the monodromy cover
Monodromy theorem
In complex analysis, the monodromy theorem is an important result about analytic continuation of a complex-analytic function to a larger set. The idea is that one can extend a complex-analytic function along curves starting in the original domain of the function and ending in the larger set...
is ramified
Ramification
In mathematics, ramification is a geometric term used for 'branching out', in the way that the square root function, for complex numbers, can be seen to have two branches differing in sign...
over the critical points (and possibly the point at infinity
Riemann sphere
In mathematics, the Riemann sphere , named after the 19th century mathematician Bernhard Riemann, is the sphere obtained from the complex plane by adding a point at infinity...
). Thus the entire function
Entire function
In complex analysis, an entire function, also called an integral function, is a complex-valued function that is holomorphic over the whole complex plane...
associated to the fi has at worst algebraic poles and ordinary algebraic branchings over the critical points.
Note that, away from the critical points, we have
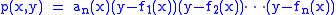
since the fi are by definition the distinct zeros of p. The monodromy group acts by permuting the factors, and thus forms the monodromy representation of the Galois group
Galois group
In mathematics, more specifically in the area of modern algebra known as Galois theory, the Galois group of a certain type of field extension is a specific group associated with the field extension...
of p. (The monodromy action on the universal covering space is related but different notion in the theory of Riemann surfaces.)
History
The ideas surrounding algebraic functions go back at least as far as René DescartesRené Descartes
René Descartes ; was a French philosopher and writer who spent most of his adult life in the Dutch Republic. He has been dubbed the 'Father of Modern Philosophy', and much subsequent Western philosophy is a response to his writings, which are studied closely to this day...
. The first discussion of algebraic functions appears to have been in Edward Waring
Edward Waring
Edward Waring was an English mathematician who was born in Old Heath , Shropshire, England and died in Pontesbury, Shropshire, England. He entered Magdalene College, Cambridge as a sizar and became Senior wrangler in 1757. He was elected a Fellow of Magdalene and in 1760 Lucasian Professor of...
's 1794 An Essay on the Principles of Human Knowledge in which he writes:
- let a quantity denoting the ordinate, be an algebraic function of the abscissa x, by the common methods of division and extraction of roots, reduce it into an infinite series ascending or descending according to the dimensions of x, and then find the integral of each of the resulting terms.