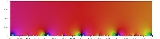
The Dedekind eta function, named after Richard Dedekind

Richard Dedekind

Julius Wilhelm Richard Dedekind was a German mathematician who did important work in abstract algebra , algebraic number theory and the foundations of the real numbers.-Life:...

, is a function defined on the upper half-plane of complex number

Complex number

A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...

s, where the imaginary part is positive. For any such complex number , we define , and define the eta function by


(The notation is now standard in number theory

Number theory

Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...

, though many older books use q for the nome ).
The presence of 24

24 (number)

24 is the natural number following 23 and preceding 25.The SI prefix for 1024 is yotta , and for 10−24 yocto...

 can be understood by connection with other occurrences, as in the modular discriminant and the Leech lattice

Leech lattice

In mathematics, the Leech lattice is an even unimodular lattice Λ24 in 24-dimensional Euclidean space E24 found by .-History:Many of the cross-sections of the Leech lattice, including the Coxeter–Todd lattice and Barnes–Wall lattice, in 12 and 16 dimensions, were found much earlier than...

.

The eta function is holomorphic on the upper half-plane but cannot be continued analytically beyond it.

The eta function satisfies the functional equation

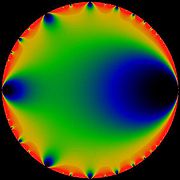
Functional equation

In mathematics, a functional equation is any equation that specifies a function in implicit form.Often, the equation relates the value of a function at some point with its values at other points. For instance, properties of functions can be determined by considering the types of functional...

s



More generally, suppose are integers with , so that


is a transformation belonging to the modular group

Modular group

In mathematics, the modular group Γ is a fundamental object of study in number theory, geometry, algebra, and many other areas of advanced mathematics...

. We may assume that either , or and . Then


where


Here is the Dedekind sum

Dedekind sum

In mathematics, Dedekind sums, named after Richard Dedekind, are certain sums of products of a sawtooth function, and are given by a function D of three integer variables. Dedekind introduced them to express the functional equation of the Dedekind eta function. They have subsequently been much...

Because of these functional equations the eta function is a modular form

Modular form

In mathematics, a modular form is a analytic function on the upper half-plane satisfying a certain kind of functional equation and growth condition. The theory of modular forms therefore belongs to complex analysis but the main importance of the theory has traditionally been in its connections...

 of weight 1/2 and level 1 for a certain character of order 24 of the metaplectic double cover

Metaplectic group

In mathematics, the metaplectic group Mp2n is a double cover of the symplectic group Sp2n. It can be defined over either real or p-adic numbers...

 of the modular group, and can be used to define other modular forms. In particular the modular discriminant of Weierstrass can be defined as


and is a modular form of weight 12. (Some authors omit the factor of (2π)¹², so that the series expansion has integral coefficients).

The Jacobi triple product implies that the eta is (up to a factor) a Jacobi theta function for special values of the arguments:


where is the Dirichlet character

Dirichlet character

In number theory, Dirichlet characters are certain arithmetic functions which arise from completely multiplicative characters on the units of \mathbb Z / k \mathbb Z...

 modulo 12 with ,
.

The Euler function


related to by , has a power series
by the Euler identity:


Because the eta function is easy to compute numerically from either power series, it is often helpful in computation to express other functions in terms of it when possible, and products and quotients of eta functions, called eta quotients, can be used to express a great variety of modular forms.

The picture on this page shows the modulus of the Euler function: the additional factor of between this and eta makes almost no visual difference whatsoever (it only introduces a tiny pinprick at the origin). Thus, this picture can be taken as a picture of eta as a function of q.

See also

• Chowla–Selberg formula
• q-series
• Weierstrass's elliptic functions
  Weierstrass's elliptic functions
  In mathematics, Weierstrass's elliptic functions are elliptic functions that take a particularly simple form; they are named for Karl Weierstrass...
  
  
• partition function (number theory)
• Kronecker limit formula
  Kronecker limit formula
  In mathematics, the classical Kronecker limit formula describes the constant term at s = 1 of a real analytic Eisenstein series in terms of the Dedekind eta function. There are many generalizations of it to more complicated Eisenstein series...
  
  
• superstring theory
  Superstring theory
  Superstring theory is an attempt to explain all of the particles and fundamental forces of nature in one theory by modelling them as vibrations of tiny supersymmetric strings...