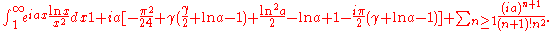Trigonometric integral
Encyclopedia
In mathematics
, the trigonometric integrals are a family of integral
s which involve trigonometric function
s. A number of the basic trigonometric integrals are discussed at the list of integrals of trigonometric functions.
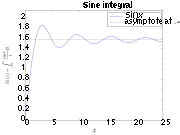The different sine
integral definitions are:
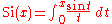
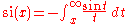
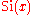is the primitive of 
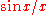which is zero for 
; 
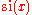is the primitive of 
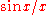which is zero for 
.
Note that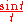
is the sinc function and also the zeroth spherical Bessel function.
When
, this is known as the Dirichlet integral
.
In signal processing
, the oscillations of the Sine integral cause overshoot
and ringing artifacts
when using the sinc filter
, and frequency domain
ringing if using a truncated sinc filter as a low-pass filter
.
The Gibbs phenomenon
is a related phenomenon: thinking of sinc as a low-pass filter
, it corresponds to truncating the Fourier series
, which causes the Gibbs phenomenon.
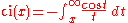
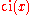is the primitive of 
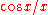which is zero for 
. We have:
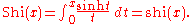
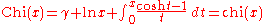
where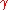
is the Euler–Mascheroni constant
.
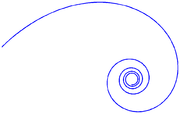The spiral
formed by parametric plot of si,ci is known as Nielsen's spiral. It is also referred to as the Euler spiral
, the Cornu spiral, a clothoid, or as a linear-curvature polynomial spiral. The spiral is also closely related to the Fresnel integral
s. This spiral has applications in vision processing, road and track construction and other areas.
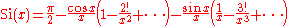
These series are divergent , although can be used for estimates and even precise evaluation at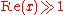
.
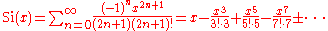
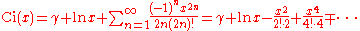
These series are convergent at any complex
, although for 
the series will converge slowly initially, requiring many terms for high precision.
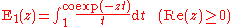is called exponential integral
. It is closely related with Si and Ci:
As each involved function is analytic except the cut at negative values of the argument,
the area of validity of the relation should be extended to
.
(Out of this range, additional terms which are integer factors of
appear in the expression).
Cases of imaginary argument of the generalized integro-exponential function are
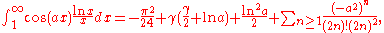
which is the real part of
Similarly
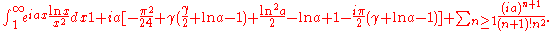
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the trigonometric integrals are a family of integral
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
s which involve trigonometric function
Trigonometric function
In mathematics, the trigonometric functions are functions of an angle. They are used to relate the angles of a triangle to the lengths of the sides of a triangle...
s. A number of the basic trigonometric integrals are discussed at the list of integrals of trigonometric functions.
Sine integral
Sine
In mathematics, the sine function is a function of an angle. In a right triangle, sine gives the ratio of the length of the side opposite to an angle to the length of the hypotenuse.Sine is usually listed first amongst the trigonometric functions....
integral definitions are:
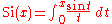
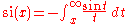
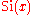is the primitive of 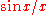which is zero for ; 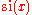is the primitive of 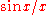which is zero for .Note that
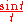is the sinc function and also the zeroth spherical Bessel function.When
, this is known as the Dirichlet integralDirichlet integral
In mathematics, there are several integrals known as the Dirichlet integral, after the German mathematician Peter Gustav Lejeune Dirichlet.One of those isThis can be derived from attempts to evaluate a double improper integral two different ways...
.
In signal processing
Signal processing
Signal processing is an area of systems engineering, electrical engineering and applied mathematics that deals with operations on or analysis of signals, in either discrete or continuous time...
, the oscillations of the Sine integral cause overshoot
Overshoot (signal)
In signal processing, control theory, electronics, and mathematics, overshoot is when a signal or function exceeds its target. It arises especially in the step response of bandlimited systems such as low-pass filters...
and ringing artifacts
Ringing artifacts
In signal processing, particularly digital image processing, ringing artifacts are artifacts that appear as spurious signals near sharp transitions in a signal. Visually, they appear as bands or "ghosts" near edges; audibly, they appear as "echos" near transients, particularly sounds from...
when using the sinc filter
Sinc filter
In signal processing, a sinc filter is an idealized filter that removes all frequency components above a given bandwidth, leaves the low frequencies alone, and has linear phase...
, and frequency domain
Frequency domain
In electronics, control systems engineering, and statistics, frequency domain is a term used to describe the domain for analysis of mathematical functions or signals with respect to frequency, rather than time....
ringing if using a truncated sinc filter as a low-pass filter
Low-pass filter
A low-pass filter is an electronic filter that passes low-frequency signals but attenuates signals with frequencies higher than the cutoff frequency. The actual amount of attenuation for each frequency varies from filter to filter. It is sometimes called a high-cut filter, or treble cut filter...
.
The Gibbs phenomenon
Gibbs phenomenon
In mathematics, the Gibbs phenomenon, named after the American physicist J. Willard Gibbs, is the peculiar manner in which the Fourier series of a piecewise continuously differentiable periodic function behaves at a jump discontinuity: the nth partial sum of the Fourier series has large...
is a related phenomenon: thinking of sinc as a low-pass filter
Low-pass filter
A low-pass filter is an electronic filter that passes low-frequency signals but attenuates signals with frequencies higher than the cutoff frequency. The actual amount of attenuation for each frequency varies from filter to filter. It is sometimes called a high-cut filter, or treble cut filter...
, it corresponds to truncating the Fourier series
Fourier series
In mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
, which causes the Gibbs phenomenon.
Cosine integral
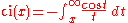
The different cosine integral definitions are: 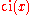is the primitive of 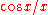which is zero for . We have:Hyperbolic sine integral
The hyperbolic sine integral: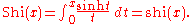Hyperbolic cosine integral
The hyperbolic cosine integral: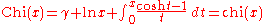where
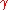is the Euler–Mascheroni constantEuler–Mascheroni constant
The Euler–Mascheroni constant is a mathematical constant recurring in analysis and number theory, usually denoted by the lowercase Greek letter ....
.
Nielsen's spiral
Spiral
In mathematics, a spiral is a curve which emanates from a central point, getting progressively farther away as it revolves around the point.-Spiral or helix:...
formed by parametric plot of si,ci is known as Nielsen's spiral. It is also referred to as the Euler spiral
Euler spiral
An Euler spiral is a curve whose curvature changes linearly with its curve length . Euler spirals are also commonly referred to as spiros, clothoids or Cornu spirals....
, the Cornu spiral, a clothoid, or as a linear-curvature polynomial spiral. The spiral is also closely related to the Fresnel integral
Fresnel integral
250px|thumb|S and C The maximum of C is about 0.977451424. If πt²/2 were used instead of t², then the image would be scaled vertically and horizontally ....
s. This spiral has applications in vision processing, road and track construction and other areas.
Expansion
Various expansions can be used for evaluation of Trigonometric integrals, depending on the range of the argument.Asymptotic series (for large argument)
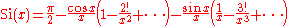
These series are divergent , although can be used for estimates and even precise evaluation at
.Convergent series
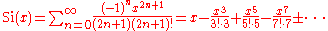
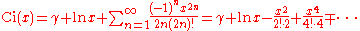
These series are convergent at any complex
, although for the series will converge slowly initially, requiring many terms for high precision.Relation with the exponential integral of imaginary argument
Function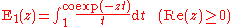 is called exponential integralExponential integral
In mathematics, the exponential integral is a special function defined on the complex plane given the symbol Ei.-Definitions:For real, nonzero values of x, the exponential integral Ei can be defined as...
. It is closely related with Si and Ci:
As each involved function is analytic except the cut at negative values of the argument,
the area of validity of the relation should be extended to
.(Out of this range, additional terms which are integer factors of
appear in the expression).Cases of imaginary argument of the generalized integro-exponential function are
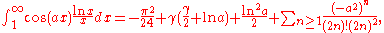
which is the real part of
Similarly