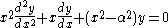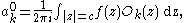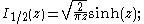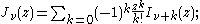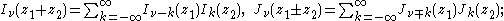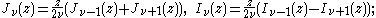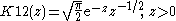
Bessel function
Encyclopedia
In mathematics, Bessel functions, first defined by the mathematician Daniel Bernoulli
and generalized by Friedrich Bessel
, are canonical solutions y(x) of Bessel's differential equation
:
for an arbitrary real or complex number α (the order of the Bessel function); the most common and important cases are for α an integer
or half-integer
.
Although α and −α produce the same differential equation, it is conventional to define different Bessel functions for these two orders (e.g., so that the Bessel functions are mostly smooth functions of α). Bessel functions are also known as cylinder functions or cylindrical harmonics because they are found in the solution to Laplace's equation
in cylindrical coordinates.
and the Helmholtz equation
in cylindrical or spherical coordinates. Bessel functions are therefore especially important for many problems of wave propagation
and static potentials. In solving problems in cylindrical coordinate systems, one obtains Bessel functions of integer order (α = n); in spherical problems, one obtains half-integer orders (α = n + ½). For example:
Bessel functions also have useful properties for other problems, such as signal processing (e.g., see FM synthesis, Kaiser window, or Bessel filter
).
expansion around x = 0:
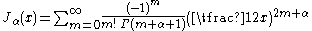
where Γ(z) is the gamma function
, a generalization of the factorial
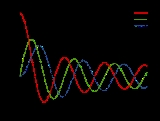
function to non-integer values. The graphs of Bessel functions look roughly like oscillating sine or cosine functions that decay proportionally to 1/√x (see also their asymptotic forms below), although their roots are not generally periodic, except asymptotically for large x. (The Taylor series indicates that −J1(x) is the derivative of J0(x), much like −sin x is the derivative of cos x; more generally, the derivative of Jn(x) can be expressed in terms of Jn±1(x) by the identities below.)
.svg.png) For non-integer α, the functions Jα(x) and J−α(x) are linearly independent, and are therefore the two solutions of the differential equation. On the other hand, for integer order α, the following relationship is valid (note that the Gamma function becomes infinite for negative integer arguments):
For non-integer α, the functions Jα(x) and J−α(x) are linearly independent, and are therefore the two solutions of the differential equation. On the other hand, for integer order α, the following relationship is valid (note that the Gamma function becomes infinite for negative integer arguments):
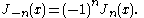
This means that the two solutions are no longer linearly independent. In this case, the second linearly independent solution is then found to be the Bessel function of the second kind, as discussed below.
 , is possible using an integral representation:
, is possible using an integral representation:
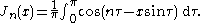
Another integral representation is:
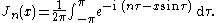
This was the approach that Bessel used, and from this definition he derived several properties of the function. The definition may be extended to non-integer orders by (for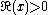 )
)
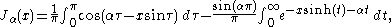
or for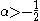 by
by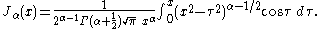
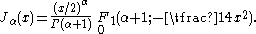
This expression is related to the development of Bessel functions in terms of the Bessel–Clifford function.
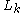 and arbitrarily chosen parameter
and arbitrarily chosen parameter  , the Bessel function can be expressed as
, the Bessel function can be expressed as
.svg.png) Yα(x) is sometimes also called the Neumann function, and is occasionally denoted instead by Nα(x). For non-integer α, it is related to Jα(x) by:
Yα(x) is sometimes also called the Neumann function, and is occasionally denoted instead by Nα(x). For non-integer α, it is related to Jα(x) by:
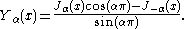
In the case of integer order n, the function is defined by taking the limit as a non-integer α tends to 'n':
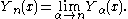
There is also a corresponding integral formula (for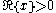 ),
),

Yα(x) is necessary as the second linearly independent solution of the Bessel's equation when α is an integer. But Yα(x) has more meaning than that. It can be considered as a 'natural' partner of Jα(x). See also the subsection on Hankel functions below.
When α is an integer, moreover, as was similarly the case for the functions of the first kind, the following relationship is valid:
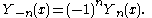
Both Jα(x) and Yα(x) are holomorphic function
s of x on the complex plane
cut along the negative real axis. When α is an integer, the Bessel functions J are entire function
s of x. If x is held fixed, then the Bessel functions are entire functions of α.
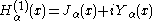

where i is the imaginary unit
. These linear combinations are also known as Bessel functions of the third kind; they are two linearly independent solutions of Bessel's differential equation. They are named after Hermann Hankel
.
The importance of Hankel functions of the first and second kind lies
more in theoretical development rather than in application. These forms of linear combination satisfy numerous simple-looking properties, like asymptotic formulae or integral representations. Here, 'simple' means an appearance of the factor of the form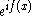 . The Bessel function of the second kind then can be thought to naturally appear as the imaginary part of the Hankel functions.
. The Bessel function of the second kind then can be thought to naturally appear as the imaginary part of the Hankel functions.
The Hankel functions are used to express outward- and inward-propagating cylindrical wave solutions of the cylindrical wave equation, respectively (or vice versa, depending on the sign convention
for the frequency
).
Using the previous relationships they can be expressed as:
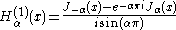
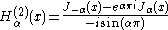
if α is an integer, the limit has to be calculated. The following relationships are valid, whether α is an integer or not:
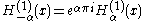
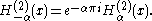
The Hankel functions admit the following integral representations for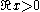 :
:
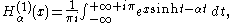
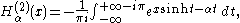
where the integration limits indicate integration along a contour
that can be chosen as follows: from −∞ to 0 along the negative real axis, from 0 to ±iπ along the imaginary axis, and from ±iπ to +∞±iπ along a contour parallel to the real axis.
arguments x, and an important special case is that of a purely imaginary argument. In this case, the solutions to the Bessel equation are called the modified Bessel functions (or occasionally the hyperbolic Bessel functions) of the first and second kind, and are defined by any of these equivalent alternatives:

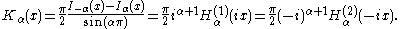
These are chosen to be real-valued for real and positive arguments x. The series expansion for Iα(x) is thus similar to that for Jα(x), but without the alternating (−1)m factor.
Iα(x) and Kα(x) are the two linearly independent solutions to the modified Bessel's equation:
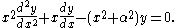
Unlike the ordinary Bessel functions, which are oscillating as functions of a real argument, Iα and Kα are exponentially growing
and decaying functions, respectively. Like the ordinary Bessel function Jα, the function Iα goes to zero at x = 0 for α > 0 and is finite at x = 0 for α = 0. Analogously, Kα diverges at x = 0.
Two integral formulas for the modified Bessel functions are (for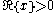 ):
):
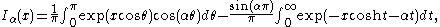
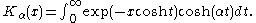
Modified Bessel functions and
and 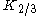 can be represented in terms of rapidly converged integrals
can be represented in terms of rapidly converged integrals
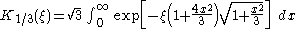

The modified Bessel function of the second kind has also been called by the now-rare names:
.svg.png)
.svg.png) When solving the Helmholtz equation
When solving the Helmholtz equation
in spherical coordinates by separation of variables, the radial equation has the form:
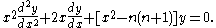
The two linearly independent solutions to this equation are called the spherical Bessel functions jn and yn, and are related to the ordinary Bessel functions Jn and Yn by:
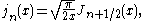
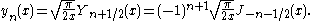
 is also denoted
is also denoted 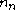 or η
or η
n; some authors call these functions the spherical Neumann functions.
The spherical Bessel functions can also be written as (Rayleigh's Formulas):
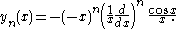
The first spherical Bessel function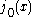 is also known as the (unnormalized) sinc function. The first few spherical Bessel functions are:
is also known as the (unnormalized) sinc function. The first few spherical Bessel functions are: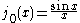
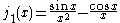
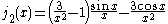
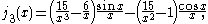
and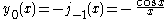
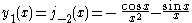
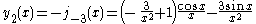
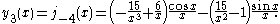
The general identities are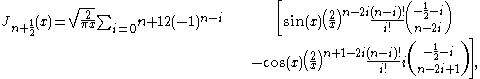
(the upper limit of summation is understood to be the largest integer less than or equal to (n+1)/2); a closed form employing Laguerre's polynomial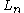 (cf. Bessel's polynomial) and other representations are provided by
(cf. Bessel's polynomial) and other representations are provided by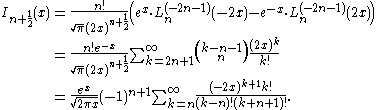
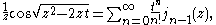
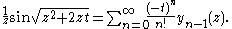
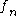 is any of
is any of 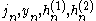 for
for 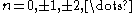
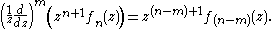
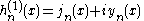
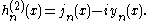
In fact, there are simple closed-form expressions for the Bessel functions of half-integer
order in terms of the standard trigonometric function
s, and therefore for the spherical Bessel functions. In particular, for non-negative integers n:
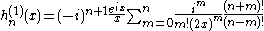
and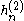 is the complex-conjugate of this (for real
is the complex-conjugate of this (for real  ). It follows, for example, that
). It follows, for example, that 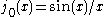 and
and 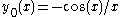 , and so on.
, and so on.
The spherical Hankel functions appear in problems involving spherical wave propagation, for example in the multipole expansion of the electromagnetic field.
–Bessel functions only slightly differ from spherical Bessel functions:
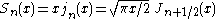
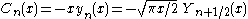
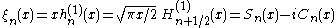
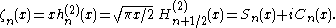
They satisfy the differential equation:
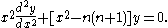
This differential equation, and the Riccati–Bessel solutions, arises in the problem of scattering of electromagnetic waves by a sphere, known as Mie scattering after the first published solution by Mie (1908). See e.g., Du (2004) for recent developments and references.
Following Debye
(1909), the notation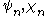 is sometimes used instead of
is sometimes used instead of
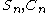 .
.
forms for non-negative α. For small arguments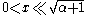 , one obtains:
, one obtains:
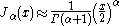
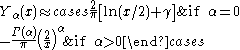
where is the Euler–Mascheroni constant
is the Euler–Mascheroni constant
(0.5772...) and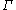 denotes the gamma function
denotes the gamma function
. For large arguments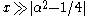 , they become:
, they become:
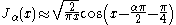

(For α=1/2 these formulas are exact; see the spherical Bessel functions above.) Asymptotic forms for the other types of Bessel function follow straightforwardly from the above relations. For example, for large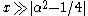 , the modified Bessel functions become:
, the modified Bessel functions become:
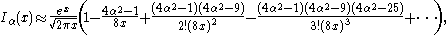
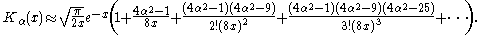
Similarly, the last expressions are exact when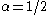 .
.
For small arguments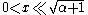 , they become:
, they become:
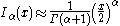
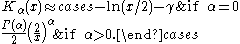
for a generating function:
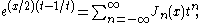
an approach used by P. A. Hansen in 1843. (This can be generalized to non-integer order by contour integration
or other methods.) Another important relation for integer orders is the Jacobi–Anger expansion:
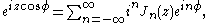
and
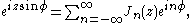
which is used to expand a plane wave
as a sum of cylindrical waves, or to find the Fourier series
of a tone-modulated FM
signal.
More generally, a series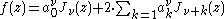
is called Neumann expansion of ƒ. The coefficients for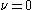 have the explicit form
have the explicit form
where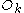 is Neumann's polynomial
is Neumann's polynomial
.
Selected functions admit the special representation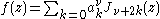
with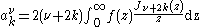
due to the orthogonality relation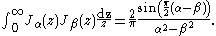
More generally, if ƒ has a branch-point near the origin of such a nature that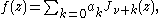 then
then
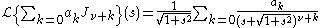
or
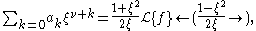
where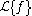 is ƒ
is ƒ' s Laplace transform.
Another way to define the Bessel functions is the Poisson representation formula and the Mehler-Sonine formula:
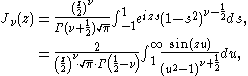
where ν > −1/2 and z is a complex number. This formula is useful especially when working with Fourier transforms.
The functions Jα, Yα, Hα(1), and Hα(2) all satisfy the recurrence relation
s:
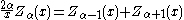

where Z denotes J, Y, H(1), or H(2). (These two identities are often combined, e.g. added or subtracted, to yield various other relations.) In this way, for example, one can compute Bessel functions of higher orders (or higher derivatives) given the values at lower orders (or lower derivatives). In particular, it follows that:
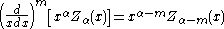
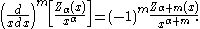
Modified Bessel functions follow similar relations :

and
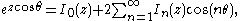
The recurrence relation reads
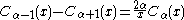
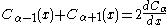
where Cα denotes Iα or eαπiKα. These recurrence relations are useful for discrete diffusion problems.
Because Bessel's equation becomes Hermitian
(self-adjoint) if it is divided by x, the solutions must satisfy an orthogonality relationship for appropriate boundary conditions. In particular, it follows that:
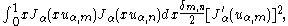
where α > −1, δm,n is the Kronecker delta, and uα,m is the m-th zero of Jα(x). This orthogonality relation can then be used to extract the coefficients in the Fourier–Bessel series, where a function is expanded in the basis of the functions Jα(x uα,m) for fixed α and varying m.
An analogous relationship for the spherical Bessel functions follows immediately:
Another orthogonality relation is the closure equation:
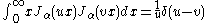
for α > −1/2 and where δ is the Dirac delta function
. This property is used to construct an arbitrary function from a series of Bessel functions by means of the Hankel transform
. For the spherical Bessel functions the orthogonality relation is:
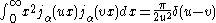
for α > −1.
Another important property of Bessel's equations, which follows from Abel's identity
, involves the Wronskian
of the solutions:
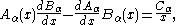
where Aα and Bα are any two solutions of Bessel's equation, and Cα is a constant independent of x (which depends on α and on the particular Bessel functions considered). For example, if Aα = Jα and Bα = Yα, then Cα is 2/π. This also holds for the modified Bessel functions; for example, if Aα = Iα and Bα = Kα, then Cα is −1.
(There are a large number of other known integrals and identities that are not reproduced here, but which can be found in the references.)
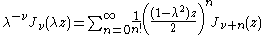
where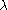 and
and  may be taken as arbitrary complex numbers. A similar form may be given for
may be taken as arbitrary complex numbers. A similar form may be given for  and etc.
and etc.
Daniel Bernoulli
Daniel Bernoulli was a Dutch-Swiss mathematician and was one of the many prominent mathematicians in the Bernoulli family. He is particularly remembered for his applications of mathematics to mechanics, especially fluid mechanics, and for his pioneering work in probability and statistics...
and generalized by Friedrich Bessel
Friedrich Bessel
-References:* John Frederick William Herschel, A brief notice of the life, researches, and discoveries of Friedrich Wilhelm Bessel, London: Barclay, 1847 -External links:...
, are canonical solutions y(x) of Bessel's differential equation
Differential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
:
for an arbitrary real or complex number α (the order of the Bessel function); the most common and important cases are for α an integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
or half-integer
Half-integer
In mathematics, a half-integer is a number of the formn + 1/2,where n is an integer. For example,are all half-integers. Note that a half of an integer is not always a half-integer: half of an even integer is an integer but not a half-integer...
.
Although α and −α produce the same differential equation, it is conventional to define different Bessel functions for these two orders (e.g., so that the Bessel functions are mostly smooth functions of α). Bessel functions are also known as cylinder functions or cylindrical harmonics because they are found in the solution to Laplace's equation
Laplace's equation
In mathematics, Laplace's equation is a second-order partial differential equation named after Pierre-Simon Laplace who first studied its properties. This is often written as:where ∆ = ∇² is the Laplace operator and \varphi is a scalar function...
in cylindrical coordinates.
Applications of Bessel function
Bessel's equation arises when finding separable solutions to Laplace's equationLaplace's equation
In mathematics, Laplace's equation is a second-order partial differential equation named after Pierre-Simon Laplace who first studied its properties. This is often written as:where ∆ = ∇² is the Laplace operator and \varphi is a scalar function...
and the Helmholtz equation
Helmholtz equation
The Helmholtz equation, named for Hermann von Helmholtz, is the elliptic partial differential equation\nabla^2 A + k^2 A = 0where ∇2 is the Laplacian, k is the wavenumber, and A is the amplitude.-Motivation and uses:...
in cylindrical or spherical coordinates. Bessel functions are therefore especially important for many problems of wave propagation
Wave propagation
Wave propagation is any of the ways in which waves travel.With respect to the direction of the oscillation relative to the propagation direction, we can distinguish between longitudinal wave and transverse waves....
and static potentials. In solving problems in cylindrical coordinate systems, one obtains Bessel functions of integer order (α = n); in spherical problems, one obtains half-integer orders (α = n + ½). For example:
- Electromagnetic wavesElectromagnetic radiationElectromagnetic radiation is a form of energy that exhibits wave-like behavior as it travels through space...
in a cylindrical waveguideWaveguideA waveguide is a structure which guides waves, such as electromagnetic waves or sound waves. There are different types of waveguides for each type of wave... - Heat conduction in a cylindrical object
- Modes of vibration of a thin circular (or annular) artificial membraneAcoustic membraneAn acoustic membrane is a thin layer that vibrates and are used in acoustics to produce or transfer sound, such as a drum, microphone, or loudspeaker....
(such as a drumDrumThe drum is a member of the percussion group of musical instruments, which is technically classified as the membranophones. Drums consist of at least one membrane, called a drumhead or drum skin, that is stretched over a shell and struck, either directly with the player's hands, or with a...
or other membranophoneMembranophoneA membranophone is any musical instrument which produces sound primarily by way of a vibrating stretched membrane. It is one of the four main divisions of instruments in the original Hornbostel-Sachs scheme of musical instrument classification....
) - Diffusion problems on a lattice
- Solutions to the radial Schrödinger equationSchrödinger equationThe Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
(in spherical and cylindrical coordinates) for a free particle - Solving for patterns of acoustical radiation
Bessel functions also have useful properties for other problems, such as signal processing (e.g., see FM synthesis, Kaiser window, or Bessel filter
Bessel filter
In electronics and signal processing, a Bessel filter is a type of linear filter with a maximally flat group delay . Bessel filters are often used in audio crossover systems...
).
Definitions
Since this is a second-order differential equation, there must be two linearly independent solutions. Depending upon the circumstances, however, various formulations of these solutions are convenient, and the different variations are described below.Bessel functions of the first kind : Jα
Bessel functions of the first kind, denoted as Jα(x), are solutions of Bessel's differential equation that are finite at the origin (x = 0) for integer α, and diverge as x approaches zero for negative non-integer α. The solution type (e.g., integer or non-integer) and normalization of Jα(x) are defined by its properties below. It is possible to define the function by its Taylor seriesTaylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
expansion around x = 0:
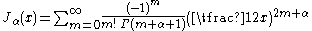
where Γ(z) is the gamma function
Gamma function
In mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...
, a generalization of the factorial
Factorial
In mathematics, the factorial of a non-negative integer n, denoted by n!, is the product of all positive integers less than or equal to n...
function to non-integer values. The graphs of Bessel functions look roughly like oscillating sine or cosine functions that decay proportionally to 1/√x (see also their asymptotic forms below), although their roots are not generally periodic, except asymptotically for large x. (The Taylor series indicates that −J1(x) is the derivative of J0(x), much like −sin x is the derivative of cos x; more generally, the derivative of Jn(x) can be expressed in terms of Jn±1(x) by the identities below.)
.svg.png)
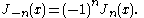
This means that the two solutions are no longer linearly independent. In this case, the second linearly independent solution is then found to be the Bessel function of the second kind, as discussed below.
Bessel's integrals
Another definition of the Bessel function, for integer values of , is possible using an integral representation:
, is possible using an integral representation: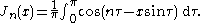
Another integral representation is:
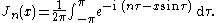
This was the approach that Bessel used, and from this definition he derived several properties of the function. The definition may be extended to non-integer orders by (for
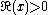 )
)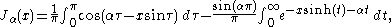
or for
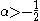 by
by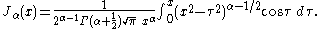
Relation to hypergeometric series
The Bessel functions can be expressed in terms of the generalized hypergeometric series as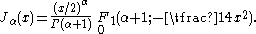
This expression is related to the development of Bessel functions in terms of the Bessel–Clifford function.
Relation to Laguerre polynomials
In terms of the Laguerre polynomialsLaguerre polynomials
In mathematics, the Laguerre polynomials, named after Edmond Laguerre ,are the canonical solutions of Laguerre's equation:x\,y + \,y' + n\,y = 0\,which is a second-order linear differential equation....
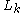 and arbitrarily chosen parameter
and arbitrarily chosen parameter  , the Bessel function can be expressed as
, the Bessel function can be expressed as
Bessel functions of the second kind : Yα
The Bessel functions of the second kind, denoted by Yα(x), are solutions of the Bessel differential equation. They have a singularity at the origin (x = 0)..svg.png)
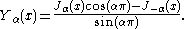
In the case of integer order n, the function is defined by taking the limit as a non-integer α tends to 'n':
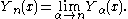
There is also a corresponding integral formula (for
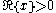 ),
),
Yα(x) is necessary as the second linearly independent solution of the Bessel's equation when α is an integer. But Yα(x) has more meaning than that. It can be considered as a 'natural' partner of Jα(x). See also the subsection on Hankel functions below.
When α is an integer, moreover, as was similarly the case for the functions of the first kind, the following relationship is valid:
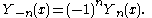
Both Jα(x) and Yα(x) are holomorphic function
Holomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
s of x on the complex plane
Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
cut along the negative real axis. When α is an integer, the Bessel functions J are entire function
Entire function
In complex analysis, an entire function, also called an integral function, is a complex-valued function that is holomorphic over the whole complex plane...
s of x. If x is held fixed, then the Bessel functions are entire functions of α.
Hankel functions: Hα(1), Hα(2)
Another important formulation of the two linearly independent solutions to Bessel's equation are the Hankel functions Hα(1)(x) and Hα(2)(x), defined by: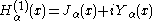

where i is the imaginary unit
Imaginary unit
In mathematics, the imaginary unit allows the real number system ℝ to be extended to the complex number system ℂ, which in turn provides at least one root for every polynomial . The imaginary unit is denoted by , , or the Greek...
. These linear combinations are also known as Bessel functions of the third kind; they are two linearly independent solutions of Bessel's differential equation. They are named after Hermann Hankel
Hermann Hankel
Hermann Hankel was a German mathematician who was born in Halle, Germany and died in Schramberg , Imperial Germany....
.
The importance of Hankel functions of the first and second kind lies
more in theoretical development rather than in application. These forms of linear combination satisfy numerous simple-looking properties, like asymptotic formulae or integral representations. Here, 'simple' means an appearance of the factor of the form
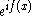 . The Bessel function of the second kind then can be thought to naturally appear as the imaginary part of the Hankel functions.
. The Bessel function of the second kind then can be thought to naturally appear as the imaginary part of the Hankel functions.The Hankel functions are used to express outward- and inward-propagating cylindrical wave solutions of the cylindrical wave equation, respectively (or vice versa, depending on the sign convention
Sign convention
In physics, a sign convention is a choice of the physical significance of signs for a set of quantities, in a case where the choice of sign is arbitrary. "Arbitrary" here means that the same physical system can be correctly described using different choices for the signs, as long as one set of...
for the frequency
Frequency
Frequency is the number of occurrences of a repeating event per unit time. It is also referred to as temporal frequency.The period is the duration of one cycle in a repeating event, so the period is the reciprocal of the frequency...
).
Using the previous relationships they can be expressed as:
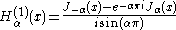
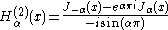
if α is an integer, the limit has to be calculated. The following relationships are valid, whether α is an integer or not:
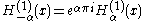
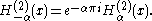
The Hankel functions admit the following integral representations for
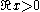 :
: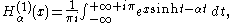
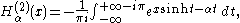
where the integration limits indicate integration along a contour
Methods of contour integration
In the mathematical field of complex analysis, contour integration is a method of evaluating certain integrals along paths in the complex plane.Contour integration is closely related to the calculus of residues, a methodology of complex analysis....
that can be chosen as follows: from −∞ to 0 along the negative real axis, from 0 to ±iπ along the imaginary axis, and from ±iπ to +∞±iπ along a contour parallel to the real axis.
Modified Bessel functions : Iα, Kα
The Bessel functions are valid even for complexComplex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
arguments x, and an important special case is that of a purely imaginary argument. In this case, the solutions to the Bessel equation are called the modified Bessel functions (or occasionally the hyperbolic Bessel functions) of the first and second kind, and are defined by any of these equivalent alternatives:

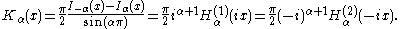
These are chosen to be real-valued for real and positive arguments x. The series expansion for Iα(x) is thus similar to that for Jα(x), but without the alternating (−1)m factor.
Iα(x) and Kα(x) are the two linearly independent solutions to the modified Bessel's equation:
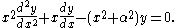
Unlike the ordinary Bessel functions, which are oscillating as functions of a real argument, Iα and Kα are exponentially growing
Exponential growth
Exponential growth occurs when the growth rate of a mathematical function is proportional to the function's current value...
and decaying functions, respectively. Like the ordinary Bessel function Jα, the function Iα goes to zero at x = 0 for α > 0 and is finite at x = 0 for α = 0. Analogously, Kα diverges at x = 0.
.svg.png) |
.svg.png) |
Two integral formulas for the modified Bessel functions are (for
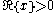 ):
):
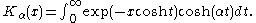
Modified Bessel functions
 and
and 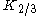 can be represented in terms of rapidly converged integrals
can be represented in terms of rapidly converged integrals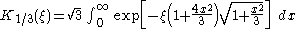

The modified Bessel function of the second kind has also been called by the now-rare names:
- Basset function
- Modified Bessel function of the third kind
- Modified Hankel function
- MacDonald function
Spherical Bessel functions: jn, yn
.svg.png)
.svg.png)
Helmholtz equation
The Helmholtz equation, named for Hermann von Helmholtz, is the elliptic partial differential equation\nabla^2 A + k^2 A = 0where ∇2 is the Laplacian, k is the wavenumber, and A is the amplitude.-Motivation and uses:...
in spherical coordinates by separation of variables, the radial equation has the form:
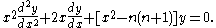
The two linearly independent solutions to this equation are called the spherical Bessel functions jn and yn, and are related to the ordinary Bessel functions Jn and Yn by:
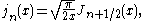
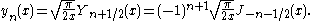
 is also denoted
is also denoted 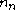 or η
or ηEta (letter)
Eta ) is the seventh letter of the Greek alphabet. Originally denoting a consonant /h/, its sound value in the classical Attic dialect of Ancient Greek was a long vowel , raised to in medieval Greek, a process known as itacism.In the system of Greek numerals it has a value of 8...
n; some authors call these functions the spherical Neumann functions.
The spherical Bessel functions can also be written as (Rayleigh's Formulas):

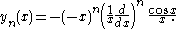
The first spherical Bessel function
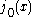 is also known as the (unnormalized) sinc function. The first few spherical Bessel functions are:
is also known as the (unnormalized) sinc function. The first few spherical Bessel functions are: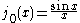
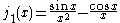
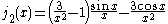
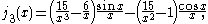
and
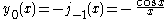
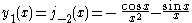
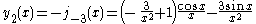
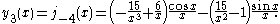
The general identities are
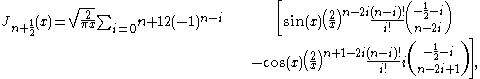
(the upper limit of summation is understood to be the largest integer less than or equal to (n+1)/2); a closed form employing Laguerre's polynomial
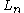 (cf. Bessel's polynomial) and other representations are provided by
(cf. Bessel's polynomial) and other representations are provided by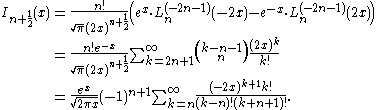
Generating function
The spherical Bessel functions have the generating functions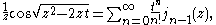
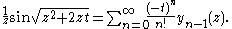
Differential relations
In the following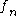 is any of
is any of 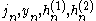 for
for 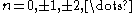
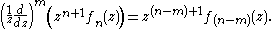
Spherical Hankel functions: hn
There are also spherical analogues of the Hankel functions: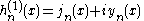
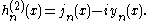
In fact, there are simple closed-form expressions for the Bessel functions of half-integer
Half-integer
In mathematics, a half-integer is a number of the formn + 1/2,where n is an integer. For example,are all half-integers. Note that a half of an integer is not always a half-integer: half of an even integer is an integer but not a half-integer...
order in terms of the standard trigonometric function
Trigonometric function
In mathematics, the trigonometric functions are functions of an angle. They are used to relate the angles of a triangle to the lengths of the sides of a triangle...
s, and therefore for the spherical Bessel functions. In particular, for non-negative integers n:
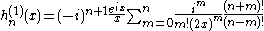
and
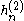 is the complex-conjugate of this (for real
is the complex-conjugate of this (for real  ). It follows, for example, that
). It follows, for example, that 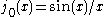 and
and 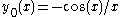 , and so on.
, and so on.The spherical Hankel functions appear in problems involving spherical wave propagation, for example in the multipole expansion of the electromagnetic field.
Riccati–Bessel functions: Sn, Cn, ξn, ζn
RiccatiJacopo Riccati
Jacopo Francesco Riccati was an Italian mathematician, born in Venice. He is now remembered for the Riccati equation. He died in Treviso in 1754.-Education:...
–Bessel functions only slightly differ from spherical Bessel functions:
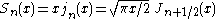
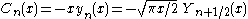
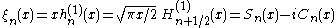
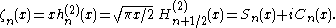
They satisfy the differential equation:
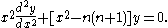
This differential equation, and the Riccati–Bessel solutions, arises in the problem of scattering of electromagnetic waves by a sphere, known as Mie scattering after the first published solution by Mie (1908). See e.g., Du (2004) for recent developments and references.
Following Debye
Peter Debye
Peter Joseph William Debye FRS was a Dutch physicist and physical chemist, and Nobel laureate in Chemistry.-Early life:...
(1909), the notation
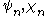 is sometimes used instead of
is sometimes used instead of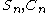 .
.Asymptotic forms
The Bessel functions have the following asymptoticAsymptotic analysis
In mathematical analysis, asymptotic analysis is a method of describing limiting behavior. The methodology has applications across science. Examples are...
forms for non-negative α. For small arguments
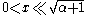 , one obtains:
, one obtains: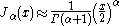
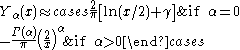
where
 is the Euler–Mascheroni constant
is the Euler–Mascheroni constantEuler–Mascheroni constant
The Euler–Mascheroni constant is a mathematical constant recurring in analysis and number theory, usually denoted by the lowercase Greek letter ....
(0.5772...) and
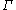 denotes the gamma function
denotes the gamma functionGamma function
In mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...
. For large arguments
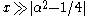 , they become:
, they become: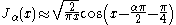

(For α=1/2 these formulas are exact; see the spherical Bessel functions above.) Asymptotic forms for the other types of Bessel function follow straightforwardly from the above relations. For example, for large
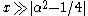 , the modified Bessel functions become:
, the modified Bessel functions become: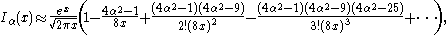
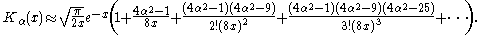
Similarly, the last expressions are exact when
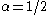 .
.For small arguments
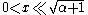 , they become:
, they become: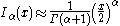
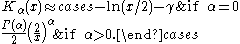
Properties
For integer order α = n, Jn is often defined via a Laurent seriesLaurent series
In mathematics, the Laurent series of a complex function f is a representation of that function as a power series which includes terms of negative degree. It may be used to express complex functions in cases where...
for a generating function:
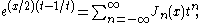
an approach used by P. A. Hansen in 1843. (This can be generalized to non-integer order by contour integration
Methods of contour integration
In the mathematical field of complex analysis, contour integration is a method of evaluating certain integrals along paths in the complex plane.Contour integration is closely related to the calculus of residues, a methodology of complex analysis....
or other methods.) Another important relation for integer orders is the Jacobi–Anger expansion:
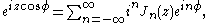
and
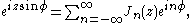
which is used to expand a plane wave
Plane wave
In the physics of wave propagation, a plane wave is a constant-frequency wave whose wavefronts are infinite parallel planes of constant peak-to-peak amplitude normal to the phase velocity vector....
as a sum of cylindrical waves, or to find the Fourier series
Fourier series
In mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
of a tone-modulated FM
Frequency modulation
In telecommunications and signal processing, frequency modulation conveys information over a carrier wave by varying its instantaneous frequency. This contrasts with amplitude modulation, in which the amplitude of the carrier is varied while its frequency remains constant...
signal.
More generally, a series
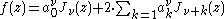
is called Neumann expansion of ƒ. The coefficients for
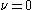 have the explicit form
have the explicit formwhere
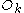 is Neumann's polynomial
is Neumann's polynomialNeumann polynomial
In mathematics, a Neumanns polynomial, introduced by Carl Neumann for the special case \alpha=0, is a polynomial in 1/z used to expand functions in term of Bessel functions....
.
Selected functions admit the special representation
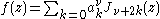
with
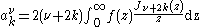
due to the orthogonality relation
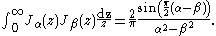
More generally, if ƒ has a branch-point near the origin of such a nature that
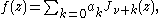 then
then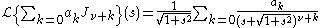
or
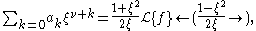
where
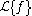 is ƒ
is ƒAnother way to define the Bessel functions is the Poisson representation formula and the Mehler-Sonine formula:
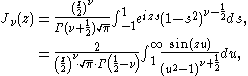
where ν > −1/2 and z is a complex number. This formula is useful especially when working with Fourier transforms.
The functions Jα, Yα, Hα(1), and Hα(2) all satisfy the recurrence relation
Recurrence relation
In mathematics, a recurrence relation is an equation that recursively defines a sequence, once one or more initial terms are given: each further term of the sequence is defined as a function of the preceding terms....
s:
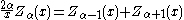

where Z denotes J, Y, H(1), or H(2). (These two identities are often combined, e.g. added or subtracted, to yield various other relations.) In this way, for example, one can compute Bessel functions of higher orders (or higher derivatives) given the values at lower orders (or lower derivatives). In particular, it follows that:
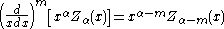
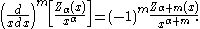
Modified Bessel functions follow similar relations :

and
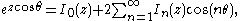
The recurrence relation reads
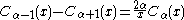
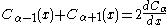
where Cα denotes Iα or eαπiKα. These recurrence relations are useful for discrete diffusion problems.
Because Bessel's equation becomes Hermitian
Hermitian
A number of mathematical entities are named Hermitian, after the mathematician Charles Hermite:*Hermitian adjoint*Hermitian connection, the unique connection on a Hermitian manifold that satisfies specific conditions...
(self-adjoint) if it is divided by x, the solutions must satisfy an orthogonality relationship for appropriate boundary conditions. In particular, it follows that:
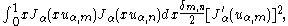
where α > −1, δm,n is the Kronecker delta, and uα,m is the m-th zero of Jα(x). This orthogonality relation can then be used to extract the coefficients in the Fourier–Bessel series, where a function is expanded in the basis of the functions Jα(x uα,m) for fixed α and varying m.
An analogous relationship for the spherical Bessel functions follows immediately:

Another orthogonality relation is the closure equation:
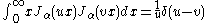
for α > −1/2 and where δ is the Dirac delta function
Dirac delta function
The Dirac delta function, or δ function, is a generalized function depending on a real parameter such that it is zero for all values of the parameter except when the parameter is zero, and its integral over the parameter from −∞ to ∞ is equal to one. It was introduced by theoretical...
. This property is used to construct an arbitrary function from a series of Bessel functions by means of the Hankel transform
Hankel transform
In mathematics, the Hankel transform expresses any given function f as the weighted sum of an infinite number of Bessel functions of the first kind Jν. The Bessel functions in the sum are all of the same order ν, but differ in a scaling factor k along the r-axis...
. For the spherical Bessel functions the orthogonality relation is:
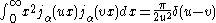
for α > −1.
Another important property of Bessel's equations, which follows from Abel's identity
Abel's identity
In mathematics, Abel's identity is an equation that expresses the Wronskian of two homogeneous solutions of a second-order linear ordinary differential equation in terms of a coefficient of the original differential equation.The relation can be generalised to nth-order linear ordinary differential...
, involves the Wronskian
Wronskian
In mathematics, the Wronskian is a determinant introduced by and named by . It is used in the study of differential equations, where it can sometimes be used to show that a set of solutions is linearly independent.-Definition:...
of the solutions:
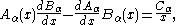
where Aα and Bα are any two solutions of Bessel's equation, and Cα is a constant independent of x (which depends on α and on the particular Bessel functions considered). For example, if Aα = Jα and Bα = Yα, then Cα is 2/π. This also holds for the modified Bessel functions; for example, if Aα = Iα and Bα = Kα, then Cα is −1.
(There are a large number of other known integrals and identities that are not reproduced here, but which can be found in the references.)
Multiplication theorem
The Bessel functions obey a multiplication theoremMultiplication theorem
In mathematics, the multiplication theorem is a certain type of identity obeyed by many special functions related to the gamma function. For the explicit case of the gamma function, the identity is a product of values; thus the name...
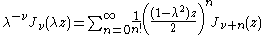
where
 and
and  may be taken as arbitrary complex numbers. A similar form may be given for
may be taken as arbitrary complex numbers. A similar form may be given for  and etc.
and etc.Bourget's hypothesis
Bessel himself originally proved that for non-negative integers n, the equation Jn(x) = 0 has an infinite number of solutions in x. When the functions Jn(x) are plotted on the same graph, though, none of the zeros seem to coincide for different values of n except for the zero at x = 0. This phenomenon is known as Bourget's hypothesis after the nineteenth century French mathematician who studied Bessel functions. Specifically it states that for any integers n ≥ 0 and m ≥ 1, the functions Jn(x) and Jn+m(x) have no common zeros other than the one at x = 0. The theorem was proved by Siegel in 1929.Selected identities
See also
- Bessel–Clifford function
- Bessel polynomialsBessel polynomialsIn mathematics, the Bessel polynomials are an orthogonal sequence of polynomials. There are a number of different but closely related definitions...
- PropagatorPropagatorIn quantum mechanics and quantum field theory, the propagator gives the probability amplitude for a particle to travel from one place to another in a given time, or to travel with a certain energy and momentum. Propagators are used to represent the contribution of virtual particles on the internal...
- Fourier–Bessel series
- Hahn–Exton q-Bessel functionHahn–Exton q-Bessel functionIn mathematics, the Hahn–Exton q-Bessel function or the third Jackson q-Bessel function is a q-analog of the Bessel function, introduced by in a special case and by in general....
- Jackson q-Bessel functionJackson q-Bessel functionIn mathematics, a Jackson q-Bessel function is one of the three q-analogs of the Bessel function introduced by...
- Struve function
- Kelvin functionsKelvin functionsIn applied mathematics, the Kelvin functions Berν and Beiν are the real and imaginary parts, respectively, ofJ_\nu,\,where x is real, and J_\nu\, is the νth order Bessel function of the first kind...
- Lommel functions
- Lommel polynomial
- Neumann polynomialNeumann polynomialIn mathematics, a Neumanns polynomial, introduced by Carl Neumann for the special case \alpha=0, is a polynomial in 1/z used to expand functions in term of Bessel functions....
- Vibrations of a circular drumVibrations of a circular drumThe vibrations of an idealized circular drum, essentially an elastic membrane of uniform thickness attached to a rigid circular frame, are solutions of the wave equation with zero boundary conditions....
- Wright generalized Bessel function
External links
- Wolfram function pages on Bessel J and Y functions, and modified Bessel I and K functions. Pages include formulas, function evaluators, and plotting calculators.
- Wolfram Mathworld – Bessel functions of the first kind