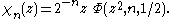Legendre chi function
Encyclopedia
In mathematics
, the Legendre chi function is a special function whose Taylor series
is also a Dirichlet series, given by

As such, it resembles the Dirichlet series for the polylogarithm, and, indeed, is trivially expressible in terms of the polylogarithm as
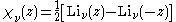
The Legendre chi function appears as the discrete fourier transform
, with respect to the order ν, of the Hurwitz zeta function, and also of the Euler polynomials, with the explicit relationships given in those articles.
The Legendre chi function is a special case of the Lerch transcendent, and is given by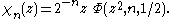
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Legendre chi function is a special function whose Taylor series
Taylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
is also a Dirichlet series, given by

As such, it resembles the Dirichlet series for the polylogarithm, and, indeed, is trivially expressible in terms of the polylogarithm as
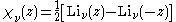
The Legendre chi function appears as the discrete fourier transform
Discrete Fourier transform
In mathematics, the discrete Fourier transform is a specific kind of discrete transform, used in Fourier analysis. It transforms one function into another, which is called the frequency domain representation, or simply the DFT, of the original function...
, with respect to the order ν, of the Hurwitz zeta function, and also of the Euler polynomials, with the explicit relationships given in those articles.
The Legendre chi function is a special case of the Lerch transcendent, and is given by