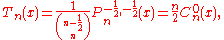Chebyshev polynomials
Encyclopedia
In mathematics
the Chebyshev polynomials, named after Pafnuty Chebyshev
, are a sequence
of orthogonal polynomials
which are related to de Moivre's formula
and which can be defined recursive
ly. One usually distinguishes between Chebyshev polynomials of the first kind which are denoted Tn and Chebyshev polynomials of the second kind which are denoted Un. The letter T is used because of the alternative transliteration
s of the name Chebyshev as Tchebycheff (French) or Tschebyschow (German).
The Chebyshev polynomials Tn or Un are polynomials of degree n and the sequence
of Chebyshev polynomials of either kind composes a polynomial sequence
.
Chebyshev polynomials are important in approximation theory
because the roots of the Chebyshev polynomials of the first kind, which are also called Chebyshev nodes
, are used as nodes in polynomial interpolation
. The resulting interpolation polynomial minimizes the problem of Runge's phenomenon
and provides an approximation that is close to the polynomial of best approximation to a continuous function
under the maximum norm. This approximation leads directly to the method of Clenshaw–Curtis quadrature.
In the study of differential equation
s they arise as the solution to the Chebyshev differential equations
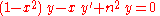
and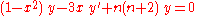
for the polynomials of the first and second kind, respectively. These equations are special cases of the Sturm–Liouville differential equation.
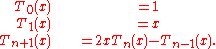
The conventional generating function
for Tn is
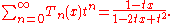
The exponential generating function is
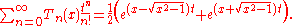
The Chebyshev polynomials of the second kind are defined by the recurrence relation
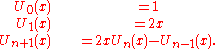
One example of a generating function
for Un is
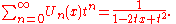
through the trigonometric
conjugacy: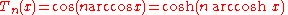
whence:
for n = 0, 1, 2, 3, ... which is a variant (equivalent transpose) of Schröder's equation,
viz. Tn(x) is functionally conjugate to nx, codified in
the nesting property below.
The polynomials of the second kind satisfy: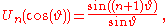
which is structurally quite similar to the Dirichlet kernel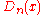 :
: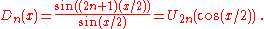
That cos(nx) is an nth-degree polynomial in cos(x) can be seen by observing that cos(nx) is the real part of one side of de Moivre's formula
, and the real part of the other side is a polynomial in cos(x) and sin(x), in which all powers of sin(x) are even and thus replaceable through the identity cos2(x) + sin2(x) = 1.
This identity is quite useful in conjunction with the recursive generating formula, inasmuch as it enables one to calculate the cosine of any integral multiple of an angle solely in terms of the cosine of the base angle.
Evaluating the first two Chebyshev polynomials: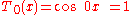
and: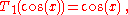
one can straightforwardly determine that:

and so forth.
Two immediate corollaries are the composition identity (or nesting property)
and the expression of complex exponentiation in terms of Chebyshev polynomials: given z = a + bi,

in a ring R[x]. Thus, they can be generated by the standard technique for Pell equations of taking powers of a fundamental solution:
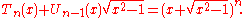
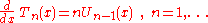
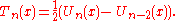
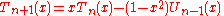

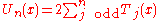 , where n is odd.
, where n is odd.
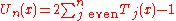 , where n is even.
, where n is even.
The recurrence relationship of the derivative of Chebyshev polynomials can be derived from these relations
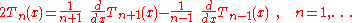
This relationship is used in the Chebyshev spectral method of solving differential equations.
Equivalently, the two sequences can also be defined from a pair of mutual recurrence equations:



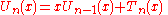
These can be derived from the trigonometric formulae; for example, if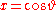 , then
, then
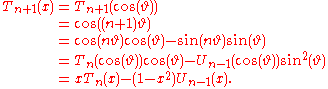
Note that both these equations and the trigonometric equations take a simpler form if we, like some works, follow the alternate convention of denoting our Un (the polynomial of degree n) with Un+1 instead.
Turán's inequalities
for the Chebyshev polynomials are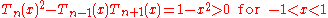 and
and
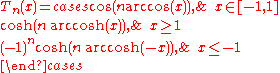
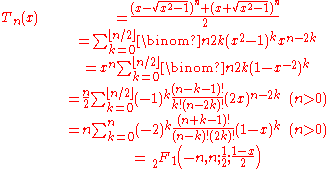
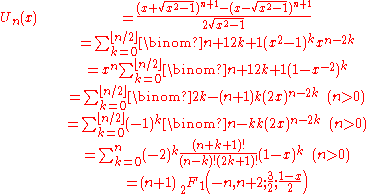
where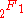 is a hypergeometric function.
is a hypergeometric function.
because they are used as nodes in polynomial interpolation. Using the trigonometric definition and the fact that
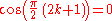
one can easily prove that the roots of Tn are

Similarly, the roots of Un are
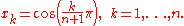
One unique property of the Chebyshev polynomials of the first kind is that on the interval all of the extrema
have values that are either −1 or 1. Thus these polynomials have only two finite critical value
s, the defining property of Shabat polynomials. Both the first and second kinds of Chebyshev polynomial have extrema at the endpoints, given by:
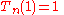
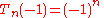
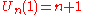
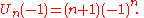

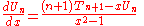

The last two formulas can be numerically troublesome due to the division by zero (0/0 indeterminate form
, specifically) at and . It can be shown that:
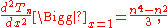

The second derivative of the Chebyshev polynomial of the first kind is
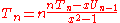
which, if evaluated as shown above, poses a problem because it is indeterminate
at x = ±1. Since the function is a polynomial, (all of) the derivatives must exist for all real numbers, so the taking to limit on the expression above should yield the desired value:

where only is considered for now. Factoring the denominator:
is considered for now. Factoring the denominator:
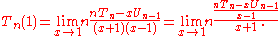
Since the limit as a whole must exist, the limit of the numerator and denominator must independently exist, and
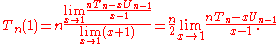
The denominator (still) limits to zero, which implies that the numerator must be limiting to zero, i.e. which will be useful later on. Since the numerator and denominator are both limiting to zero, L'Hôpital's rule
which will be useful later on. Since the numerator and denominator are both limiting to zero, L'Hôpital's rule
applies:
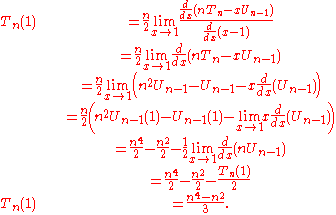
The proof for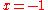 is similar, with the fact that
is similar, with the fact that 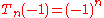 being important.
being important.
Indeed, the following, more general formula holds:
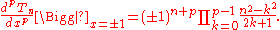
This latter result is of great use in the numerical solution of eigenvalue problems.
Concerning integration, the first derivative of the Tn implies that
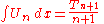
and the recurrence relation for the first kind polynomials involving derivatives establishes that
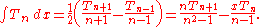
. The polynomials of the first kind are orthogonal with respect to the weight

on the interval (−1,1), i.e. we have:
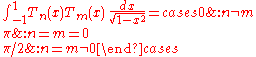
This can be proven by letting and using the identity
and using the identity
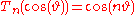 .
.
Similarly, the polynomials of the second kind are orthogonal with respect to the weight

on the interval [−1,1], i.e. we have:
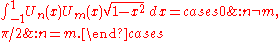
(Note that the weight is, to within a normalizing constant, the density of the Wigner semicircle distribution).
is, to within a normalizing constant, the density of the Wigner semicircle distribution).
The Tn also satisfy a discrete orthogonality condition:
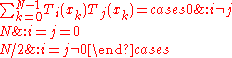
where the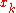 are the N Gauss
are the N Gauss
–Lobatto
zeros of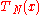


is the one of which the maximal absolute value on the interval [−1, 1] is minimal.
This maximal absolute value is
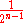
and |ƒ(x)| reaches this maximum exactly times at
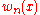 is a polynomial of degree n with leading coefficient 1 with maximal absolute value on the interval [−1, 1] less than
is a polynomial of degree n with leading coefficient 1 with maximal absolute value on the interval [−1, 1] less than  .
.
We define

Because at extreme points of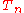 we have
we have 
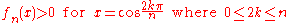
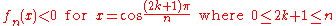
From the intermediate value theorem
,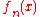 has at least n roots. However, this is impossible, as
has at least n roots. However, this is impossible, as 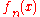 is a polynomial of degree , so the fundamental theorem of algebra
is a polynomial of degree , so the fundamental theorem of algebra
implies it has at most roots.
, which themselves are a special case of the Jacobi polynomials
:
For every nonnegative integer n, Tn(x) and Un(x) are both polynomials of degree n. They are even or odd functions
of x as n is even or odd, so when written as polynomials of x, it only has even or odd degree terms respectively. In fact,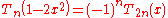
and
The leading coefficient of Tn is if , but 1 if .
Tn are a special case of Lissajous curve
s with frequency ratio equal to n.
Several polynomial sequences like Lucas polynomials (Ln), Dickson polynomials(Dn), Fibonacci polynomials(Fn) are related to Chebyshev polynomials Tn and Un.
The Chebyshev polynomials of the first kind satisfy the relation
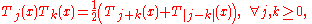
which is easily proved from the product-to-sum formula for the cosine. The polynomials of the second kind satisfy the similar relation
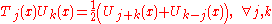 .
.
Similar to the formula
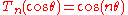
we have the analogous formula
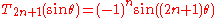 .
.
Let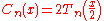 .
.
Then and
and 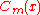 are commuting polynomials:
are commuting polynomials: .
.
).svg.png) The first few Chebyshev polynomials of the first kind are
The first few Chebyshev polynomials of the first kind are

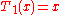
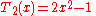

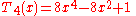
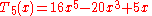


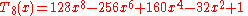

).svg.png) The first few Chebyshev polynomials of the second kind are
The first few Chebyshev polynomials of the second kind are

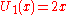
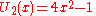
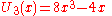
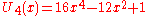
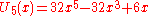
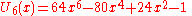
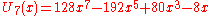
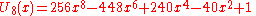
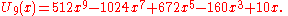
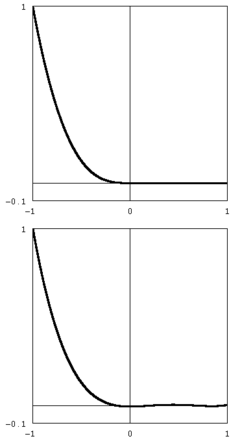 In the appropriate Sobolev space
In the appropriate Sobolev space
, the set of Chebyshev polynomials form a complete basis set
, so that a function in the same space can, on be expressed via the expansion:

Furthermore, as mentioned previously, the Chebyshev polynomials form an orthogonal basis which (among other things) implies that the coefficients an can be determined easily through the application of an inner product. This sum is called a Chebyshev series or a Chebyshev expansion.
Since a Chebyshev series is related to a Fourier cosine series through a change of variables, all of the theorems, identities, etc. that apply to Fourier series
have a Chebyshev counterpart. These attributes include:
The abundance of the theorems and identities inherited from Fourier series
make the Chebyshev polynomials important tools in numeric analysis; for example they are the most popular general purpose basis functions used in the spectral method
, often in favor of trigonometric series due to generally faster convergence for continuous functions (Gibbs' phenomenon is still a problem).
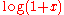 . One can express
. One can express

One can find the coefficients either through the application of an inner product or by the discrete orthogonality condition. For the inner product,
either through the application of an inner product or by the discrete orthogonality condition. For the inner product,
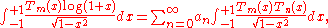
which gives
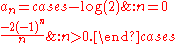
Alternatively, when you cannot evaluate the inner product of the function you are trying to approximate, the discrete orthogonality condition gives
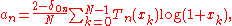
where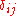 is the Kronecker delta function and the
is the Kronecker delta function and the 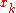 are the N Gauss–Lobatto zeros of
are the N Gauss–Lobatto zeros of 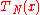
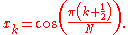
This allows us to compute the coefficients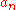 very efficiently through the discrete cosine transform
very efficiently through the discrete cosine transform
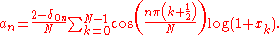


are very useful in the approximation
of various functions and in the solution of differential equation
s (see spectral method
). Two common methods for determining the coefficients an are through the use of the inner product as in Galerkin's method and through the use of collocation
which is related to interpolation
.
As an interpolant, the N coefficients of the partial sum are usually obtained on the Chebyshev–Gauss–Lobatto points (or Lobatto grid), which results in minimum error and avoids Runge's phenomenon
associated with a uniform grid. This collection of points corresponds to the extrema of the highest order polynomial in the sum, plus the endpoints and is given by:
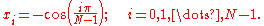

Polynomials in Chebyshev form can be evaluated using the Clenshaw algorithm
.
are in a sense equivalent to the Chebyshev polynomials of the first kind, but enable one to avoid square roots and conventional trigonometric functions in certain contexts, notably in rational trigonometry
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
the Chebyshev polynomials, named after Pafnuty Chebyshev
Pafnuty Chebyshev
Pafnuty Lvovich Chebyshev was a Russian mathematician. His name can be alternatively transliterated as Chebychev, Chebysheff, Chebyshov, Tschebyshev, Tchebycheff, or Tschebyscheff .-Early years:One of nine children, Chebyshev was born in the village of Okatovo in the district of Borovsk,...
, are a sequence
Polynomial sequence
In mathematics, a polynomial sequence is a sequence of polynomials indexed by the nonnegative integers 0, 1, 2, 3, ..., in which each index is equal to the degree of the corresponding polynomial...
of orthogonal polynomials
Orthogonal polynomials
In mathematics, the classical orthogonal polynomials are the most widely used orthogonal polynomials, and consist of the Hermite polynomials, the Laguerre polynomials, the Jacobi polynomials together with their special cases the ultraspherical polynomials, the Chebyshev polynomials, and the...
which are related to de Moivre's formula
De Moivre's formula
In mathematics, de Moivre's formula , named after Abraham de Moivre, states that for any complex number x and integer n it holds that...
and which can be defined recursive
Recursion
Recursion is the process of repeating items in a self-similar way. For instance, when the surfaces of two mirrors are exactly parallel with each other the nested images that occur are a form of infinite recursion. The term has a variety of meanings specific to a variety of disciplines ranging from...
ly. One usually distinguishes between Chebyshev polynomials of the first kind which are denoted Tn and Chebyshev polynomials of the second kind which are denoted Un. The letter T is used because of the alternative transliteration
Transliteration
Transliteration is a subset of the science of hermeneutics. It is a form of translation, and is the practice of converting a text from one script into another...
s of the name Chebyshev as Tchebycheff (French) or Tschebyschow (German).
The Chebyshev polynomials Tn or Un are polynomials of degree n and the sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
of Chebyshev polynomials of either kind composes a polynomial sequence
Polynomial sequence
In mathematics, a polynomial sequence is a sequence of polynomials indexed by the nonnegative integers 0, 1, 2, 3, ..., in which each index is equal to the degree of the corresponding polynomial...
.
Chebyshev polynomials are important in approximation theory
Approximation theory
In mathematics, approximation theory is concerned with how functions can best be approximated with simpler functions, and with quantitatively characterizing the errors introduced thereby...
because the roots of the Chebyshev polynomials of the first kind, which are also called Chebyshev nodes
Chebyshev nodes
In numerical analysis, Chebyshev nodes are the roots of the Chebyshev polynomial of the first kind. They are often used as nodes in polynomial interpolation because the resulting interpolation polynomial minimizes the Runge's phenomenon.-Definition:...
, are used as nodes in polynomial interpolation
Polynomial interpolation
In numerical analysis, polynomial interpolation is the interpolation of a given data set by a polynomial: given some points, find a polynomial which goes exactly through these points.- Applications :...
. The resulting interpolation polynomial minimizes the problem of Runge's phenomenon
Runge's phenomenon
In the mathematical field of numerical analysis, Runge's phenomenon is a problem of oscillation at the edges of an interval that occurs when using polynomial interpolation with polynomials of high degree...
and provides an approximation that is close to the polynomial of best approximation to a continuous function
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
under the maximum norm. This approximation leads directly to the method of Clenshaw–Curtis quadrature.
In the study of differential equation
Differential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
s they arise as the solution to the Chebyshev differential equations
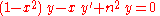
and
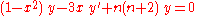
for the polynomials of the first and second kind, respectively. These equations are special cases of the Sturm–Liouville differential equation.
Definition
The Chebyshev polynomials of the first kind are defined by the recurrence relationRecurrence relation
In mathematics, a recurrence relation is an equation that recursively defines a sequence, once one or more initial terms are given: each further term of the sequence is defined as a function of the preceding terms....
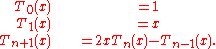
The conventional generating function
Generating function
In mathematics, a generating function is a formal power series in one indeterminate, whose coefficients encode information about a sequence of numbers an that is indexed by the natural numbers. Generating functions were first introduced by Abraham de Moivre in 1730, in order to solve the general...
for Tn is
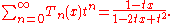
The exponential generating function is
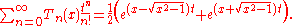
The Chebyshev polynomials of the second kind are defined by the recurrence relation
Recurrence relation
In mathematics, a recurrence relation is an equation that recursively defines a sequence, once one or more initial terms are given: each further term of the sequence is defined as a function of the preceding terms....
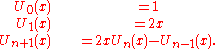
One example of a generating function
Generating function
In mathematics, a generating function is a formal power series in one indeterminate, whose coefficients encode information about a sequence of numbers an that is indexed by the natural numbers. Generating functions were first introduced by Abraham de Moivre in 1730, in order to solve the general...
for Un is
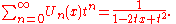
Trigonometric definition
The Chebyshev polynomials of the first kind can be defined compactly in an orbitOrbit
In physics, an orbit is the gravitationally curved path of an object around a point in space, for example the orbit of a planet around the center of a star system, such as the Solar System...
through the trigonometric
conjugacy:
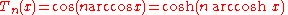
whence:

for n = 0, 1, 2, 3, ... which is a variant (equivalent transpose) of Schröder's equation,
viz. Tn(x) is functionally conjugate to nx, codified in
the nesting property below.
The polynomials of the second kind satisfy:
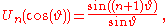
which is structurally quite similar to the Dirichlet kernel
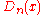 :
: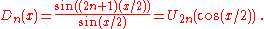
That cos(nx) is an nth-degree polynomial in cos(x) can be seen by observing that cos(nx) is the real part of one side of de Moivre's formula
De Moivre's formula
In mathematics, de Moivre's formula , named after Abraham de Moivre, states that for any complex number x and integer n it holds that...
, and the real part of the other side is a polynomial in cos(x) and sin(x), in which all powers of sin(x) are even and thus replaceable through the identity cos2(x) + sin2(x) = 1.
This identity is quite useful in conjunction with the recursive generating formula, inasmuch as it enables one to calculate the cosine of any integral multiple of an angle solely in terms of the cosine of the base angle.
Evaluating the first two Chebyshev polynomials:
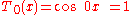
and:
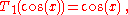
one can straightforwardly determine that:


and so forth.
Two immediate corollaries are the composition identity (or nesting property)
and the expression of complex exponentiation in terms of Chebyshev polynomials: given z = a + bi,

Pell equation definition
The Chebyshev polynomials can also be defined as the solutions to the Pell equation
in a ring R[x]. Thus, they can be generated by the standard technique for Pell equations of taking powers of a fundamental solution:
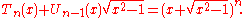
Relation between Chebyshev polynomials of the first and second kinds
The Chebyshev polynomials of the first and second kind are closely related by the following equations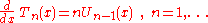
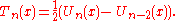
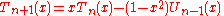

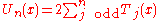 , where n is odd.
, where n is odd.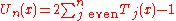 , where n is even.
, where n is even.The recurrence relationship of the derivative of Chebyshev polynomials can be derived from these relations
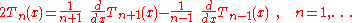
This relationship is used in the Chebyshev spectral method of solving differential equations.
Equivalently, the two sequences can also be defined from a pair of mutual recurrence equations:



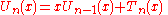
These can be derived from the trigonometric formulae; for example, if
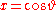 , then
, then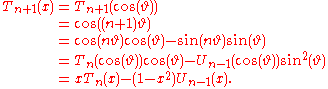
Note that both these equations and the trigonometric equations take a simpler form if we, like some works, follow the alternate convention of denoting our Un (the polynomial of degree n) with Un+1 instead.
Turán's inequalities
Turán's inequalities
In mathematics, Turán's inequalities are some inequalities for Legendre polynomials found by . There are many generalizations to other polynomials, often called Turán's inequalities, given by and other authors....
for the Chebyshev polynomials are
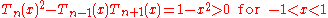 and
and
Explicit formulas
Different approaches to defining Chebyshev polynomials lead to different explicit formulas such as: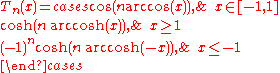
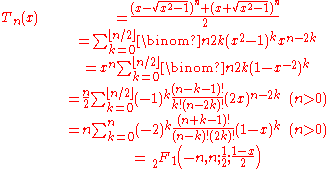
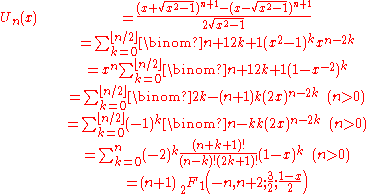
where
 is a hypergeometric function.
is a hypergeometric function.Roots and extrema
A Chebyshev polynomial of either kind with degree n has n different simple roots, called Chebyshev roots, in the interval [−1,1]. The roots are sometimes called Chebyshev nodesChebyshev nodes
In numerical analysis, Chebyshev nodes are the roots of the Chebyshev polynomial of the first kind. They are often used as nodes in polynomial interpolation because the resulting interpolation polynomial minimizes the Runge's phenomenon.-Definition:...
because they are used as nodes in polynomial interpolation. Using the trigonometric definition and the fact that
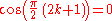
one can easily prove that the roots of Tn are

Similarly, the roots of Un are
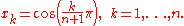
One unique property of the Chebyshev polynomials of the first kind is that on the interval all of the extrema
Maxima and minima
In mathematics, the maximum and minimum of a function, known collectively as extrema , are the largest and smallest value that the function takes at a point either within a given neighborhood or on the function domain in its entirety .More generally, the...
have values that are either −1 or 1. Thus these polynomials have only two finite critical value
Critical value
-Differential topology:In differential topology, a critical value of a differentiable function between differentiable manifolds is the image ƒ in N of a critical point x in M.The basic result on critical values is Sard's lemma...
s, the defining property of Shabat polynomials. Both the first and second kinds of Chebyshev polynomial have extrema at the endpoints, given by:
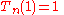
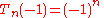
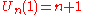
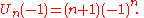
Differentiation and integration
The derivatives of the polynomials can be less than straightforward. By differentiating the polynomials in their trigonometric forms, it's easy to show that:
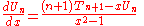

The last two formulas can be numerically troublesome due to the division by zero (0/0 indeterminate form
Indeterminate form
In calculus and other branches of mathematical analysis, an indeterminate form is an algebraic expression obtained in the context of limits. Limits involving algebraic operations are often performed by replacing subexpressions by their limits; if the expression obtained after this substitution...
, specifically) at and . It can be shown that:
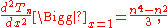

The second derivative of the Chebyshev polynomial of the first kind is
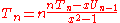
which, if evaluated as shown above, poses a problem because it is indeterminate
Indeterminate form
In calculus and other branches of mathematical analysis, an indeterminate form is an algebraic expression obtained in the context of limits. Limits involving algebraic operations are often performed by replacing subexpressions by their limits; if the expression obtained after this substitution...
at x = ±1. Since the function is a polynomial, (all of) the derivatives must exist for all real numbers, so the taking to limit on the expression above should yield the desired value:

where only
 is considered for now. Factoring the denominator:
is considered for now. Factoring the denominator: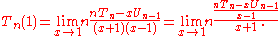
Since the limit as a whole must exist, the limit of the numerator and denominator must independently exist, and
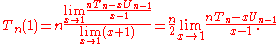
The denominator (still) limits to zero, which implies that the numerator must be limiting to zero, i.e.
 which will be useful later on. Since the numerator and denominator are both limiting to zero, L'Hôpital's rule
which will be useful later on. Since the numerator and denominator are both limiting to zero, L'Hôpital's ruleL'Hôpital's rule
In calculus, l'Hôpital's rule uses derivatives to help evaluate limits involving indeterminate forms. Application of the rule often converts an indeterminate form to a determinate form, allowing easy evaluation of the limit...
applies:
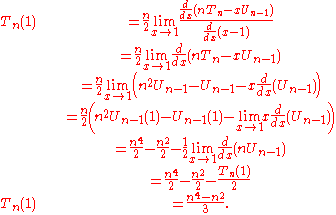
The proof for
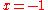 is similar, with the fact that
is similar, with the fact that 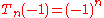 being important.
being important.Indeed, the following, more general formula holds:
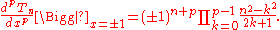
This latter result is of great use in the numerical solution of eigenvalue problems.
Concerning integration, the first derivative of the Tn implies that
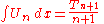
and the recurrence relation for the first kind polynomials involving derivatives establishes that
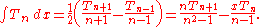
Orthogonality
Both the Tn and the Un form a sequence of orthogonal polynomialsOrthogonal polynomials
In mathematics, the classical orthogonal polynomials are the most widely used orthogonal polynomials, and consist of the Hermite polynomials, the Laguerre polynomials, the Jacobi polynomials together with their special cases the ultraspherical polynomials, the Chebyshev polynomials, and the...
. The polynomials of the first kind are orthogonal with respect to the weight

on the interval (−1,1), i.e. we have:
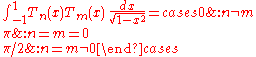
This can be proven by letting
 and using the identity
and using the identity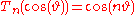 .
.Similarly, the polynomials of the second kind are orthogonal with respect to the weight

on the interval [−1,1], i.e. we have:
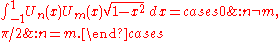
(Note that the weight
 is, to within a normalizing constant, the density of the Wigner semicircle distribution).
is, to within a normalizing constant, the density of the Wigner semicircle distribution).The Tn also satisfy a discrete orthogonality condition:
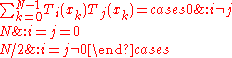
where the
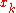 are the N Gauss
are the N GaussCarl Friedrich Gauss
Johann Carl Friedrich Gauss was a German mathematician and scientist who contributed significantly to many fields, including number theory, statistics, analysis, differential geometry, geodesy, geophysics, electrostatics, astronomy and optics.Sometimes referred to as the Princeps mathematicorum...
–Lobatto
Rehuel Lobatto
Rehuel Lobatto was a Dutch mathematician. Lobatto was born in Amsterdam to a Portuguese Marrano family. As a schoolboy Lobatto already displayed remarkable talent for mathematics...
zeros of
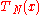

Minimal ∞-norm
For any given n ≥ 1, among the polynomials of degree n with leading coefficient 1,
is the one of which the maximal absolute value on the interval [−1, 1] is minimal.
This maximal absolute value is
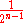
and |ƒ(x)| reaches this maximum exactly times at
Proof
Let's assume that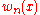 is a polynomial of degree n with leading coefficient 1 with maximal absolute value on the interval [−1, 1] less than
is a polynomial of degree n with leading coefficient 1 with maximal absolute value on the interval [−1, 1] less than  .
.We define

Because at extreme points of
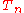 we have
we have 
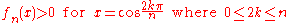
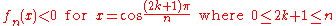
From the intermediate value theorem
Intermediate value theorem
In mathematical analysis, the intermediate value theorem states that for each value between the least upper bound and greatest lower bound of the image of a continuous function there is at least one point in its domain that the function maps to that value....
,
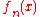 has at least n roots. However, this is impossible, as
has at least n roots. However, this is impossible, as 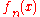 is a polynomial of degree , so the fundamental theorem of algebra
is a polynomial of degree , so the fundamental theorem of algebraFundamental theorem of algebra
The fundamental theorem of algebra states that every non-constant single-variable polynomial with complex coefficients has at least one complex root...
implies it has at most roots.
Other properties
The Chebyshev polynomials are a special case of the ultraspherical or Gegenbauer polynomialsGegenbauer polynomials
In mathematics, Gegenbauer polynomials or ultraspherical polynomials C are orthogonal polynomials on the interval [−1,1] with respect to the weight function α–1/2. They generalize Legendre polynomials and Chebyshev polynomials, and are special cases of Jacobi polynomials...
, which themselves are a special case of the Jacobi polynomials
Jacobi polynomials
In mathematics, Jacobi polynomials are a class of classical orthogonal polynomials. They are orthogonal with respect to the weight ^\alpha ^\beta on the interval [-1, 1]...
:
For every nonnegative integer n, Tn(x) and Un(x) are both polynomials of degree n. They are even or odd functions
Even and odd functions
In mathematics, even functions and odd functions are functions which satisfy particular symmetry relations, with respect to taking additive inverses. They are important in many areas of mathematical analysis, especially the theory of power series and Fourier series...
of x as n is even or odd, so when written as polynomials of x, it only has even or odd degree terms respectively. In fact,
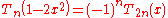
and

The leading coefficient of Tn is if , but 1 if .
Tn are a special case of Lissajous curve
Lissajous curve
In mathematics, a Lissajous curve , also known as Lissajous figure or Bowditch curve, is the graph of a system of parametric equationswhich describe complex harmonic motion...
s with frequency ratio equal to n.
Several polynomial sequences like Lucas polynomials (Ln), Dickson polynomials(Dn), Fibonacci polynomials(Fn) are related to Chebyshev polynomials Tn and Un.
The Chebyshev polynomials of the first kind satisfy the relation
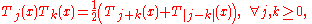
which is easily proved from the product-to-sum formula for the cosine. The polynomials of the second kind satisfy the similar relation
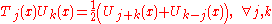 .
.Similar to the formula
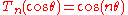
we have the analogous formula
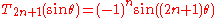 .
.Let
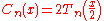 .
.Then
 and
and 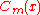 are commuting polynomials:
are commuting polynomials: .
.Examples
).svg.png)

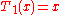
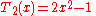

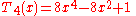
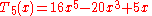


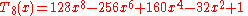

).svg.png)

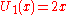
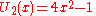
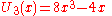
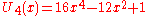
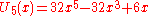
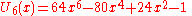
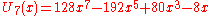
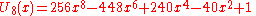
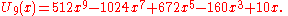
As a basis set

Sobolev space
In mathematics, a Sobolev space is a vector space of functions equipped with a norm that is a combination of Lp-norms of the function itself as well as its derivatives up to a given order. The derivatives are understood in a suitable weak sense to make the space complete, thus a Banach space...
, the set of Chebyshev polynomials form a complete basis set
Basis set
Basis set can refer to:* Basis * Basis set...
, so that a function in the same space can, on be expressed via the expansion:

Furthermore, as mentioned previously, the Chebyshev polynomials form an orthogonal basis which (among other things) implies that the coefficients an can be determined easily through the application of an inner product. This sum is called a Chebyshev series or a Chebyshev expansion.
Since a Chebyshev series is related to a Fourier cosine series through a change of variables, all of the theorems, identities, etc. that apply to Fourier series
Fourier series
In mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
have a Chebyshev counterpart. These attributes include:
- The Chebyshev polynomials form a complete orthogonal system.
- The Chebyshev series converges to ƒ(x) if the function is piecewisePiecewiseOn mathematics, a piecewise-defined function is a function whose definition changes depending on the value of the independent variable...
smoothSmooth functionIn mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
and continuousContinuous functionIn mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
. The smoothness requirement can be relaxed in most cases — as long as there are a finite number of discontinuities in ƒ(x) and its derivatives. - At a discontinuity, the series will converge to the average of the right and left limits.
The abundance of the theorems and identities inherited from Fourier series
Fourier series
In mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
make the Chebyshev polynomials important tools in numeric analysis; for example they are the most popular general purpose basis functions used in the spectral method
Spectral method
Spectral methods are a class of techniques used in applied mathematics and scientific computing to numerically solve certain Dynamical Systems, often involving the use of the Fast Fourier Transform. Where applicable, spectral methods have excellent error properties, with the so called "exponential...
, often in favor of trigonometric series due to generally faster convergence for continuous functions (Gibbs' phenomenon is still a problem).
Example 1
Consider the Chebyshev expansion of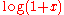 . One can express
. One can express
One can find the coefficients
 either through the application of an inner product or by the discrete orthogonality condition. For the inner product,
either through the application of an inner product or by the discrete orthogonality condition. For the inner product,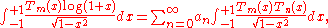
which gives
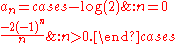
Alternatively, when you cannot evaluate the inner product of the function you are trying to approximate, the discrete orthogonality condition gives
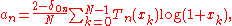
where
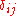 is the Kronecker delta function and the
is the Kronecker delta function and the 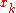 are the N Gauss–Lobatto zeros of
are the N Gauss–Lobatto zeros of 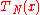
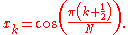
This allows us to compute the coefficients
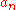 very efficiently through the discrete cosine transform
very efficiently through the discrete cosine transformDiscrete cosine transform
A discrete cosine transform expresses a sequence of finitely many data points in terms of a sum of cosine functions oscillating at different frequencies. DCTs are important to numerous applications in science and engineering, from lossy compression of audio and images A discrete cosine transform...
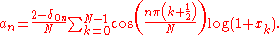
Example 2
To provide another example:
Partial sums
The partial sums of
are very useful in the approximation
Approximation theory
In mathematics, approximation theory is concerned with how functions can best be approximated with simpler functions, and with quantitatively characterizing the errors introduced thereby...
of various functions and in the solution of differential equation
Differential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
s (see spectral method
Spectral method
Spectral methods are a class of techniques used in applied mathematics and scientific computing to numerically solve certain Dynamical Systems, often involving the use of the Fast Fourier Transform. Where applicable, spectral methods have excellent error properties, with the so called "exponential...
). Two common methods for determining the coefficients an are through the use of the inner product as in Galerkin's method and through the use of collocation
Collocation method
In mathematics, a collocation method is a method for the numerical solution of ordinary differential equations, partial differential equations and integral equations...
which is related to interpolation
Interpolation
In the mathematical field of numerical analysis, interpolation is a method of constructing new data points within the range of a discrete set of known data points....
.
As an interpolant, the N coefficients of the partial sum are usually obtained on the Chebyshev–Gauss–Lobatto points (or Lobatto grid), which results in minimum error and avoids Runge's phenomenon
Runge's phenomenon
In the mathematical field of numerical analysis, Runge's phenomenon is a problem of oscillation at the edges of an interval that occurs when using polynomial interpolation with polynomials of high degree...
associated with a uniform grid. This collection of points corresponds to the extrema of the highest order polynomial in the sum, plus the endpoints and is given by:
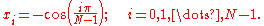
Polynomial in Chebyshev form
An arbitrary polynomial of degree N can be written in terms of the Chebyshev polynomials of the first kind. Such a polynomial p(x) is of the form
Polynomials in Chebyshev form can be evaluated using the Clenshaw algorithm
Clenshaw algorithm
In numerical analysis, the Clenshaw algorithm is a recursive method to evaluate a linear combination of Chebyshev polynomials. In general it applies to any class of functions that can be defined by a three-term recurrence relation.-Clenshaw algorithm:...
.
Spread polynomials
The spread polynomialsSpread polynomials
In the conventional language of trigonometry, the nth-degree spread polynomial Sn, for n = 0, 1, 2, ..., may be characterized by the trigonometric identity\sin^2 = S_n.\,...
are in a sense equivalent to the Chebyshev polynomials of the first kind, but enable one to avoid square roots and conventional trigonometric functions in certain contexts, notably in rational trigonometry
Rational trigonometry
Rational trigonometry is a recently introduced approach to trigonometry that eschews all transcendental functions and all proportional measurements of angles. In place of angles, it characterizes the separation between lines by a quantity called the "spread", which is a rational function of their...
.
See also
- Chebyshev nodesChebyshev nodesIn numerical analysis, Chebyshev nodes are the roots of the Chebyshev polynomial of the first kind. They are often used as nodes in polynomial interpolation because the resulting interpolation polynomial minimizes the Runge's phenomenon.-Definition:...
- Chebyshev filterChebyshev filterChebyshev filters are analog or digital filters having a steeper roll-off and more passband ripple or stopband ripple than Butterworth filters...
- Chebyshev cube root
- Dickson polynomials
- Legendre polynomials
- Hermite polynomialsHermite polynomialsIn mathematics, the Hermite polynomials are a classical orthogonal polynomial sequence that arise in probability, such as the Edgeworth series; in combinatorics, as an example of an Appell sequence, obeying the umbral calculus; in numerical analysis as Gaussian quadrature; and in physics, where...
- Chebyshev rational functionsChebyshev rational functionsIn mathematics, the Chebyshev rational functions are a sequence of functions which are both rational and orthogonal. They are named after Pafnuty Chebyshev...
- Clenshaw–Curtis quadrature
- Approximation theoryApproximation theoryIn mathematics, approximation theory is concerned with how functions can best be approximated with simpler functions, and with quantitatively characterizing the errors introduced thereby...
- The Chebfun systemChebfunChebfun is a freely available software system written in MATLAB for numerical computation with functions of a real variable. It is based on the idea of overloading MATLAB's commands for vectors and matrices to analogous commands for functions and operators...
External links
- Module for Chebyshev Polynomials by John H. Mathews
- Chebyshev Interpolation: An Interactive Tour, includes illustrative Java appletJava appletA Java applet is an applet delivered to users in the form of Java bytecode. Java applets can run in a Web browser using a Java Virtual Machine , or in Sun's AppletViewer, a stand-alone tool for testing applets...
. - Numerical Computing with Functions: The Chebfun Project