Super-logarithm
Encyclopedia
In mathematics
, the super-logarithm is one of the two inverse functions of tetration
. Just as exponentiation
has two inverse functions, roots
and logarithms, tetration
has two inverse functions, super-roots and super-logarithms. There are several ways of interpreting super-logarithms:
The precise definition of the super-logarithm depends on a precise definition of non-integral tetration
(that is,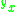 for y not an integer). There is no clear consensus on the definition of non-integral tetration
for y not an integer). There is no clear consensus on the definition of non-integral tetration
and so there is likewise no clear consensus on the super-logarithm for non-integer range
.
 , is defined implicitly by
, is defined implicitly by
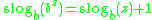 and
and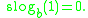
Notice that this definition can only have integer outputs, and will only accept values that will produce integer outputs. The only numbers that this definition will accept are of the form and so on. In order to extend the domain of the super-logarithm from this sparse set to the real numbers, several approaches have been pursued. These usually include a third requirement in addition to those listed above, which vary from author to author. These approaches are as follows:
and so on. In order to extend the domain of the super-logarithm from this sparse set to the real numbers, several approaches have been pursued. These usually include a third requirement in addition to those listed above, which vary from author to author. These approaches are as follows:
are defined not only for the real values of argument(s), but to complex plane, and differential and/or integral representation, as well as expansions in convergent and asymptotic series. Yet, no such representations are available for the slog function. Nevertheless, the simple approximations below are suggested.
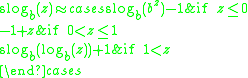
which is a piecewise-defined function with a linear "critical piece". This function has the property that it is continuous for all real z ( continuous). The first authors to recognize this approximation were Rubstov and Romerio, although it is not in their paper, it can be found in their algorithm that is used in their software prototype. The linear approximation to tetration
continuous). The first authors to recognize this approximation were Rubstov and Romerio, although it is not in their paper, it can be found in their algorithm that is used in their software prototype. The linear approximation to tetration
, on the other hand, had been known before, for example by Ioannis Galidakis. This is a natural inverse of the linear approximation to tetration
.
Authors like Holmes recognize that the super-logarithm would be a great use to the next evolution of computer floating-point arithmetic, but for this purpose, the function need not be infinitely differentiable. Thus, for the purpose of representing large numbers, the linear approximation approach provides enough continuity ( continuity) to ensure that all real numbers can be represented on a super-logarithmic scale.
continuity) to ensure that all real numbers can be represented on a super-logarithmic scale.
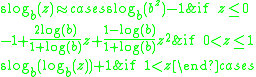
which is a piecewise-defined function with a quadratic "critical piece". This function has the property that it is continuous and differentiable for all real z ( continuous). The first author to publish this approximation was Andrew Robbins in this paper.
continuous). The first author to publish this approximation was Andrew Robbins in this paper.
This version of the super-logarithm allows for basic calculus operations to be performed on the super-logarithm, without requiring a large amount of solving beforehand. Using this method, basic investigation of the properties of the super-logarithm and tetration
can be performed with a small amount of computational overhead.
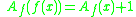
Given an Abel function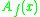 another solution can be obtained by adding any constant
another solution can be obtained by adding any constant 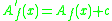 . Thus given that the super-logarithm is defined by
. Thus given that the super-logarithm is defined by 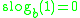 and the third special property that differs between approaches, the Abel function of the exponential function could be uniquely determined.
and the third special property that differs between approaches, the Abel function of the exponential function could be uniquely determined.
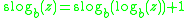
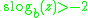 for all real z
for all real z
Probably the first example of mathematical problem where the solution is expressed in terms of super-logarithms, is the following:
 As tetration
As tetration
(or super-exponential)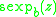 is suspected to be an analytic function
is suspected to be an analytic function
, at least for some values of , the inverse function
, the inverse function
slogb=sexpb−1 may also be analytic.
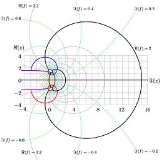
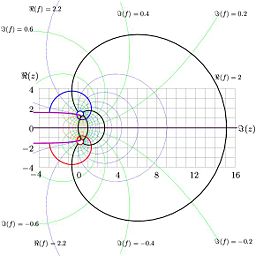
Behavior of
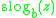 , defined in such a way, the complex
, defined in such a way, the complex  plane is sketched in Figure 1
plane is sketched in Figure 1
for the case . Levels of integer values of real and integer values
. Levels of integer values of real and integer values
of imaginary parts of the slog functions are shown with thick lines.
If the existence and uniqueness of the analytic extension of tetration
is provided by the condition of its
asymptotic approach to the fixed points
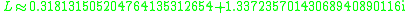 and
and
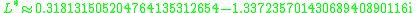
of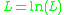
in the upper and lower parts of the complex plane, then the inverse function should also be unique.
Such a function is real at the real axis. It has two branch point
s at
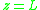 and
and
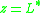 . It approaches its limiting value
. It approaches its limiting value 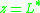 in vicinity of the negative part of the real
in vicinity of the negative part of the real
axis (all the strip between the cuts shown with pink lines in the figure), and slowly grows up along the positive
direction of the real axis.
As the derivative at the real axis is positive, the imaginary part of slog remains positive
just above the real axis and negative just below the real axis.
The existence, uniqueness and generalizations are under discussion
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the super-logarithm is one of the two inverse functions of tetration
Tetration
In mathematics, tetration is an iterated exponential and is the next hyper operator after exponentiation. The word tetration was coined by English mathematician Reuben Louis Goodstein from tetra- and iteration. Tetration is used for the notation of very large numbers...
. Just as exponentiation
Exponentiation
Exponentiation is a mathematical operation, written as an, involving two numbers, the base a and the exponent n...
has two inverse functions, roots
Nth root
In mathematics, the nth root of a number x is a number r which, when raised to the power of n, equals xr^n = x,where n is the degree of the root...
and logarithms, tetration
Tetration
In mathematics, tetration is an iterated exponential and is the next hyper operator after exponentiation. The word tetration was coined by English mathematician Reuben Louis Goodstein from tetra- and iteration. Tetration is used for the notation of very large numbers...
has two inverse functions, super-roots and super-logarithms. There are several ways of interpreting super-logarithms:
- As the Abel functionAbel functionIn mathematics Abel function is a special kind of solution of the Abel equations, used to classify them as superfunctions, and formulate conditions of uniqueness.The Abel equation is class of equations which can be written in the formg=g+1...
of exponential functionExponential functionIn mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
s, - As the inverse function of tetrationTetrationIn mathematics, tetration is an iterated exponential and is the next hyper operator after exponentiation. The word tetration was coined by English mathematician Reuben Louis Goodstein from tetra- and iteration. Tetration is used for the notation of very large numbers...
with respect to the height, - As the number of times a logarithmLogarithmThe logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
must be iteratedIterated functionIn mathematics, an iterated function is a function which is composed with itself, possibly ad infinitum, in a process called iteration. In this process, starting from some initial value, the result of applying a given function is fed again in the function as input, and this process is repeated...
to get to 1 (the Iterated logarithmIterated logarithmIn computer science, the iterated logarithm of n, written n , is the number of times the logarithm function must be iteratively applied before the result is less than or equal to 1...
), - As a generalization of Robert Munafo's large number class system,
- As an unbounded version of the logistic functionLogistic functionA logistic function or logistic curve is a common sigmoid curve, given its name in 1844 or 1845 by Pierre François Verhulst who studied it in relation to population growth. It can model the "S-shaped" curve of growth of some population P...
.
The precise definition of the super-logarithm depends on a precise definition of non-integral tetration
Tetration
In mathematics, tetration is an iterated exponential and is the next hyper operator after exponentiation. The word tetration was coined by English mathematician Reuben Louis Goodstein from tetra- and iteration. Tetration is used for the notation of very large numbers...
(that is,
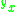 for y not an integer). There is no clear consensus on the definition of non-integral tetration
for y not an integer). There is no clear consensus on the definition of non-integral tetrationTetration
In mathematics, tetration is an iterated exponential and is the next hyper operator after exponentiation. The word tetration was coined by English mathematician Reuben Louis Goodstein from tetra- and iteration. Tetration is used for the notation of very large numbers...
and so there is likewise no clear consensus on the super-logarithm for non-integer range
Range (mathematics)
In mathematics, the range of a function refers to either the codomain or the image of the function, depending upon usage. This ambiguity is illustrated by the function f that maps real numbers to real numbers with f = x^2. Some books say that range of this function is its codomain, the set of all...
.
Definitions
The super-logarithm, written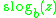 , is defined implicitly by
, is defined implicitly by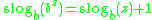 and
and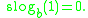
Notice that this definition can only have integer outputs, and will only accept values that will produce integer outputs. The only numbers that this definition will accept are of the form
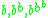 and so on. In order to extend the domain of the super-logarithm from this sparse set to the real numbers, several approaches have been pursued. These usually include a third requirement in addition to those listed above, which vary from author to author. These approaches are as follows:
and so on. In order to extend the domain of the super-logarithm from this sparse set to the real numbers, several approaches have been pursued. These usually include a third requirement in addition to those listed above, which vary from author to author. These approaches are as follows:- The linear approximation approach by Rubstov and Romerio,
- The quadratic approximation approach by Andrew Robbins,
- The regular Abel function approach by George Szekeres,
- The iterative functional approach by Peter Walker, and
- The natural matrix approach by Peter Walker, and later generalized by Andrew Robbins.
Approximations
Usually, the special functionsSpecial functions
Special functions are particular mathematical functions which have more or less established names and notations due to their importance in mathematical analysis, functional analysis, physics, or other applications....
are defined not only for the real values of argument(s), but to complex plane, and differential and/or integral representation, as well as expansions in convergent and asymptotic series. Yet, no such representations are available for the slog function. Nevertheless, the simple approximations below are suggested.
Linear approximation
The linear approximation to the super-logarithm is: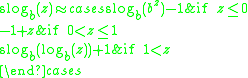
which is a piecewise-defined function with a linear "critical piece". This function has the property that it is continuous for all real z (
 continuous). The first authors to recognize this approximation were Rubstov and Romerio, although it is not in their paper, it can be found in their algorithm that is used in their software prototype. The linear approximation to tetration
continuous). The first authors to recognize this approximation were Rubstov and Romerio, although it is not in their paper, it can be found in their algorithm that is used in their software prototype. The linear approximation to tetrationTetration
In mathematics, tetration is an iterated exponential and is the next hyper operator after exponentiation. The word tetration was coined by English mathematician Reuben Louis Goodstein from tetra- and iteration. Tetration is used for the notation of very large numbers...
, on the other hand, had been known before, for example by Ioannis Galidakis. This is a natural inverse of the linear approximation to tetration
Tetration
In mathematics, tetration is an iterated exponential and is the next hyper operator after exponentiation. The word tetration was coined by English mathematician Reuben Louis Goodstein from tetra- and iteration. Tetration is used for the notation of very large numbers...
.
Authors like Holmes recognize that the super-logarithm would be a great use to the next evolution of computer floating-point arithmetic, but for this purpose, the function need not be infinitely differentiable. Thus, for the purpose of representing large numbers, the linear approximation approach provides enough continuity (
 continuity) to ensure that all real numbers can be represented on a super-logarithmic scale.
continuity) to ensure that all real numbers can be represented on a super-logarithmic scale.Quadratic approximation
The quadratic approximation to the super-logarithm is: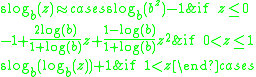
which is a piecewise-defined function with a quadratic "critical piece". This function has the property that it is continuous and differentiable for all real z (
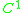 continuous). The first author to publish this approximation was Andrew Robbins in this paper.
continuous). The first author to publish this approximation was Andrew Robbins in this paper.This version of the super-logarithm allows for basic calculus operations to be performed on the super-logarithm, without requiring a large amount of solving beforehand. Using this method, basic investigation of the properties of the super-logarithm and tetration
Tetration
In mathematics, tetration is an iterated exponential and is the next hyper operator after exponentiation. The word tetration was coined by English mathematician Reuben Louis Goodstein from tetra- and iteration. Tetration is used for the notation of very large numbers...
can be performed with a small amount of computational overhead.
Approaches to the Abel function
The Abel function is any function that satisfies Abel's functional equation: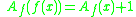
Given an Abel function
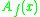 another solution can be obtained by adding any constant
another solution can be obtained by adding any constant 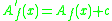 . Thus given that the super-logarithm is defined by
. Thus given that the super-logarithm is defined by 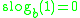 and the third special property that differs between approaches, the Abel function of the exponential function could be uniquely determined.
and the third special property that differs between approaches, the Abel function of the exponential function could be uniquely determined.Properties
Other equations that the super-logarithm satisfies are: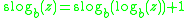
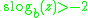 for all real z
for all real zProbably the first example of mathematical problem where the solution is expressed in terms of super-logarithms, is the following:
- Consider oriented graphs with N nodes and such that oriented path from node i to node j exists if and only if
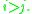 If length of all such paths is at most k edges, then the minimum possible total number of edges is:
If length of all such paths is at most k edges, then the minimum possible total number of edges is:
-
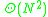 for
for 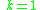
-
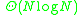 for
for 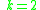
-
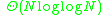 for
for 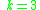
-
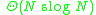 for
for 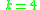 and
and 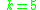
-
slog as inverse of tetration

Tetration
In mathematics, tetration is an iterated exponential and is the next hyper operator after exponentiation. The word tetration was coined by English mathematician Reuben Louis Goodstein from tetra- and iteration. Tetration is used for the notation of very large numbers...
(or super-exponential)
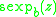 is suspected to be an analytic function
is suspected to be an analytic function, at least for some values of
 , the inverse function
, the inverse functionslogb=sexpb−1 may also be analytic.
Behavior of
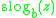 , defined in such a way, the complex
, defined in such a way, the complex  plane is sketched in Figure 1
plane is sketched in Figure 1for the case
 . Levels of integer values of real and integer values
. Levels of integer values of real and integer valuesof imaginary parts of the slog functions are shown with thick lines.
If the existence and uniqueness of the analytic extension of tetration
Tetration
In mathematics, tetration is an iterated exponential and is the next hyper operator after exponentiation. The word tetration was coined by English mathematician Reuben Louis Goodstein from tetra- and iteration. Tetration is used for the notation of very large numbers...
is provided by the condition of its
asymptotic approach to the fixed points
Fixed point (mathematics)
In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...
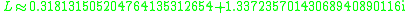 and
and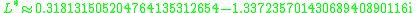
of
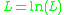
in the upper and lower parts of the complex plane, then the inverse function should also be unique.
Such a function is real at the real axis. It has two branch point
Branch point
In the mathematical field of complex analysis, a branch point of a multi-valued function is a point such that the function is discontinuous when going around an arbitrarily small circuit around this point...
s at
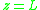 and
and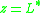 . It approaches its limiting value
. It approaches its limiting value 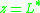 in vicinity of the negative part of the real
in vicinity of the negative part of the realaxis (all the strip between the cuts shown with pink lines in the figure), and slowly grows up along the positive
direction of the real axis.
As the derivative at the real axis is positive, the imaginary part of slog remains positive
just above the real axis and negative just below the real axis.
The existence, uniqueness and generalizations are under discussion
.
External links
- Rubstov and Romerio, Hyper-operations Thread 1
- Rubstov and Romerio, Hyper-operations Thread 2

