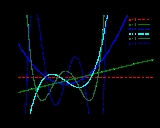
Hermite polynomials
Overview
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Hermite polynomials are a classical orthogonal
Orthogonal polynomials
In mathematics, the classical orthogonal polynomials are the most widely used orthogonal polynomials, and consist of the Hermite polynomials, the Laguerre polynomials, the Jacobi polynomials together with their special cases the ultraspherical polynomials, the Chebyshev polynomials, and the...
polynomial sequence
Polynomial sequence
In mathematics, a polynomial sequence is a sequence of polynomials indexed by the nonnegative integers 0, 1, 2, 3, ..., in which each index is equal to the degree of the corresponding polynomial...
that arise in probability
Probability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
, such as the Edgeworth series
Edgeworth series
The Gram–Charlier A series , and the Edgeworth series are series that approximate a probability distribution in terms of its cumulants...
; in combinatorics
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
, as an example of an Appell sequence, obeying the umbral calculus
Umbral calculus
In mathematics before the 1970s, the term umbral calculus referred to the surprising similarity between seemingly unrelated polynomial equations and certain shadowy techniques used to 'prove' them. These techniques were introduced by and are sometimes called Blissard's symbolic method...
; in numerical analysis as Gaussian quadrature
Gaussian quadrature
In numerical analysis, a quadrature rule is an approximation of the definite integral of a function, usually stated as a weighted sum of function values at specified points within the domain of integration....
; and in physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, where they give rise to the eigenstates of the quantum harmonic oscillator
Quantum harmonic oscillator
The quantum harmonic oscillator is the quantum-mechanical analog of the classical harmonic oscillator. Because an arbitrary potential can be approximated as a harmonic potential at the vicinity of a stable equilibrium point, it is one of the most important model systems in quantum mechanics...
. They are also used in systems theory in connection with nonlinear operations on Gaussian noise
Gaussian noise
Gaussian noise is statistical noise that has its probability density function equal to that of the normal distribution, which is also known as the Gaussian distribution. In other words, the values that the noise can take on are Gaussian-distributed. A special case is white Gaussian noise, in which...
. They are named after Charles Hermite
Charles Hermite
Charles Hermite was a French mathematician who did research on number theory, quadratic forms, invariant theory, orthogonal polynomials, elliptic functions, and algebra....
(1864) although they were studied earlier by and Chebyshev (1859).
There are two different standard ways of normalizing Hermite polynomials:
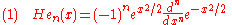
(the "probabilists' Hermite polynomials"), and

(the "physicists' Hermite polynomials").
Unanswered Questions

