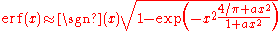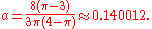Error function
Encyclopedia
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the error function (also called the Gauss error function) is a special function
(non-elementary) of sigmoid
Sigmoid function
Many natural processes, including those of complex system learning curves, exhibit a progression from small beginnings that accelerates and approaches a climax over time. When a detailed description is lacking, a sigmoid function is often used. A sigmoid curve is produced by a mathematical...
shape which occurs in probability
Probability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
, statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
and partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
s. It is defined as:
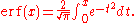
The complementary error function, denoted erfc, is defined as
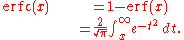
The imaginary error function, denoted erfi, is defined as
The complex error function, denoted w(x) and also known as the Faddeeva function, is defined as
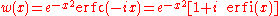
The Name "Error Function"
The error function is used in measurement theory (using probability and statistics), and although its use in other branches of mathematics has nothing to do with the characterization of measurement errors, the name has stuck.The error function is the integral of the Gaussian function curve (the "bell curve" or "normal distribution"). As a result, the error function gives the probability that a measurement, under the influence of accidental errors, has a distance less than x from the average value at the center. This function is used in statistics to predict behavior of any sample with respect to the population mean. This usage is similar to the Q-function
Q-function
In statistics, the Q-function is the tail probability of the standard normal distribution. In other words, Q is the probability that a standard normal random variable will obtain a value larger than x...
, which in fact can be written in terms of the error function.
Properties
The error function is oddEven and odd functions
In mathematics, even functions and odd functions are functions which satisfy particular symmetry relations, with respect to taking additive inverses. They are important in many areas of mathematical analysis, especially the theory of power series and Fourier series...
:
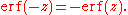
Also, for any complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
z:
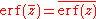
where
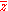is the complex conjugateComplex conjugate
In mathematics, complex conjugates are a pair of complex numbers, both having the same real part, but with imaginary parts of equal magnitude and opposite signs...
of z.
The integrand ƒ = exp(−z2) and ƒ = erf(z) are shown in the complex z-plane in figures 2 and 3. Level of Im(ƒ) = 0 is shown with a thick green line.
Negative integer values of Im(ƒ) are shown with thick red lines. Positive integer values of
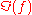are shown with thick blue lines. Intermediate levels of Im(ƒ) = constant are shown with thin green lines.Intermediate levels of Re(ƒ) = constant are shown with thin red lines for negative values and with thin blue lines for positive values.
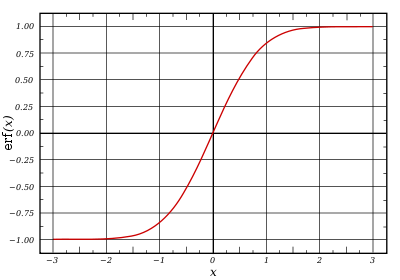
At the real axis, erf(z) approaches unity at z → +∞ and −1 at z → −∞. At the imaginary axis, it tends to ±i∞.
Taylor series
The error function is an entire functionEntire function
In complex analysis, an entire function, also called an integral function, is a complex-valued function that is holomorphic over the whole complex plane...
; it has no singularities (except that at infinity) and its Taylor expansion always converges.
The defining integral cannot be evaluated in closed form
Closed-form expression
In mathematics, an expression is said to be a closed-form expression if it can be expressed analytically in terms of a bounded number of certain "well-known" functions...
in terms of elementary functions
Elementary function (differential algebra)
In mathematics, an elementary function is a function of one variable built from a finite number of exponentials, logarithms, constants, and nth roots through composition and combinations using the four elementary operations...
, but by expanding the integrand e−z2 into its Taylor series and integrating term by term, one obtains the error function's Taylor series as:
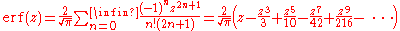
which holds for every complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
z. The denominator terms are sequence A007680 in the OEIS.
For iterative calculation of the above series, the following alternative formulation may be useful:
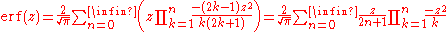
because
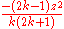expresses the multiplier to turn the kth term into the (k + 1)th term (considering z as the first term).The error function at +∞ is exactly 1 (see Gaussian integral
Gaussian integral
The Gaussian integral, also known as the Euler-Poisson integral or Poisson integral, is the integral of the Gaussian function e−x2 over the entire real line.It is named after the German mathematician and...
).
The derivative of the error function follows immediately from its definition:
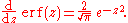
An antiderivative
Antiderivative
In calculus, an "anti-derivative", antiderivative, primitive integral or indefinite integralof a function f is a function F whose derivative is equal to f, i.e., F ′ = f...
of the error function is
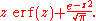
Inverse functions
The inverse error function is defined as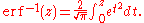
and has series
where c0 = 1 and
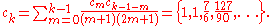
So we have the series expansion (note that common factors have been canceled from numerators and denominators):
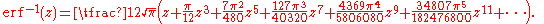
(After cancellation the numerator/denominator fractions are entries A092676/A132467 in the OEIS; without cancellation the numerator terms are given in entry A002067.) Note that the error function's value at ±∞ is equal to ±1.
The inverse complementary error function is defined as
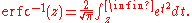
Asymptotic expansion
A useful asymptotic expansionAsymptotic expansion
In mathematics an asymptotic expansion, asymptotic series or Poincaré expansion is a formal series of functions which has the property that truncating the series after a finite number of terms provides an approximation to a given function as the argument of the function tends towards a particular,...
of the complementary error function (and therefore also of the error function) for large x is
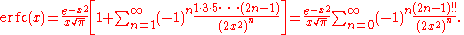
This series diverges for every finite x, and its meaning as asymptotic expansion is that, for any
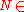one has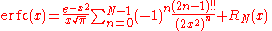
where the remainder, in Landau notation, is
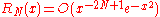as 
.Indeed, the exact value of the remainder is
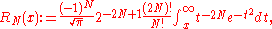
which follows easily by induction, writing
and integrating by parts.For large enough values of x, only the first few terms of this asymptotic expansion are needed to obtain a good approximation of erfc(x) (while for not too large values of x note that the above Taylor expansion at 0 provides a very fast convergence).
Continued fractions expansion
A continued fractions expansion of the complementary error function is :
Approximation with elementary functions
Abramowitz and StegunAbramowitz and Stegun
Abramowitz and Stegun is the informal name of a mathematical reference work edited by Milton Abramowitz and Irene Stegun of the U.S. National Bureau of Standards...
give several approximations of varying accuracy (equations 7.1.25-28). This allows one to choose the fastest approximation suitable for a given application. In order of increasing accuracy, they are:
-
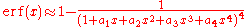(maximum error: 5·10-4)
where a1=0.278393, a2=0.230389, a3=0.000972, a4=0.078108
-
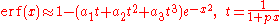(maximum error: 2.5·10-5)
where p=0.47047, a1=0.3480242, a2=-0.0958798, a3=0.7478556
-
(maximum error: 3·10-7)
where a1=0.0705230784, a2=0.0422820123, a3=0.0092705272, a4=0.0001520143, a5=0.0002765672, a6=0.0000430638
-
(maximum error: 1.5·10-7)
where p=0.3275911, a1=0.254829592, a2=-0.284496736, a3=1.421413741, a4=-1.453152027, a5=1.061405429
All of these approximations are valid for x≥0. To use these approximations for negative x, use the fact that erf(x) is an odd function, so erf(x)=-erf(-x).
Another approximation is given by
where
This is designed to be very accurate in a neighborhood of 0 and a neighborhood of infinity, and the error is less than 0.00035 for all x. Using the alternate value a ≈ 0.147 reduces the maximum error to about 0.00012.
This approximation can also be inverted to calculate the inverse error function:
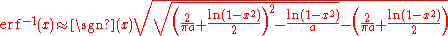
Applications
When the results of a series of measurements are described by a normal distribution with standard deviationStandard deviation
Standard deviation is a widely used measure of variability or diversity used in statistics and probability theory. It shows how much variation or "dispersion" there is from the average...
and expected valueExpected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
0, then
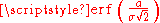is the probability that the error of a single measurement lies between −a and +a, for positive a. This is useful, for example, in determining the bit error rate of a digital communication system.The error and complementary error functions occur, for example, in solutions of the heat equation
Heat equation
The heat equation is an important partial differential equation which describes the distribution of heat in a given region over time...
when boundary conditions are given by the Heaviside step function
Heaviside step function
The Heaviside step function, or the unit step function, usually denoted by H , is a discontinuous function whose value is zero for negative argument and one for positive argument....
.
Related functions
The error function is essentially identical to the standard normal cumulative distribution function, denoted Φ, also named norm(x) by software languages, as they differ only by scaling and translation.Indeed,
or rearranged for erf and erfc:
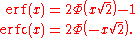
Consequently, the error function is also closely related to the Q-function
Q-function
In statistics, the Q-function is the tail probability of the standard normal distribution. In other words, Q is the probability that a standard normal random variable will obtain a value larger than x...
, which is the tail probability of the standard normal distribution. The Q-function can be expressed in terms of the error function as
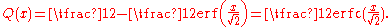
The inverse
Inverse function
In mathematics, an inverse function is a function that undoes another function: If an input x into the function ƒ produces an output y, then putting y into the inverse function g produces the output x, and vice versa. i.e., ƒ=y, and g=x...
of
is known as the normal quantile functionQuantile function
In probability and statistics, the quantile function of the probability distribution of a random variable specifies, for a given probability, the value which the random variable will be at, or below, with that probability...
, or probit
Probit
In probability theory and statistics, the probit function is the inverse cumulative distribution function , or quantile function associated with the standard normal distribution...
function and may be expressed in terms of the inverse error function as
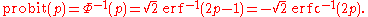
The standard normal cdf is used more often in probability and statistics, and the error function is used more often in other branches of mathematics.
The error function is a special case of the Mittag-Leffler function
Mittag-Leffler function
In mathematics, the Mittag-Leffler function Eα,β is a special function, a complex function which depends on two complex parameters α and β...
, and can also be expressed as a confluent hypergeometric function
Confluent hypergeometric function
In mathematics, a confluent hypergeometric function is a solution of a confluent hypergeometric equation, which is a degenerate form of a hypergeometric differential equation where two of the three regular singularities merge into an irregular singularity...
(Kummer's function):
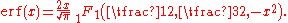
It has a simple expression in terms of the Fresnel integral
Fresnel integral
250px|thumb|S and C The maximum of C is about 0.977451424. If πt²/2 were used instead of t², then the image would be scaled vertically and horizontally ....
. In terms of the Regularized Gamma function P and the incomplete gamma function
Incomplete gamma function
In mathematics, the gamma function is defined by a definite integral. The incomplete gamma function is defined as an integral function of the same integrand. There are two varieties of the incomplete gamma function: the upper incomplete gamma function is for the case that the lower limit of...
,
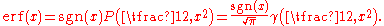
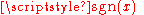is the sign functionSign function
In mathematics, the sign function is an odd mathematical function that extracts the sign of a real number. To avoid confusion with the sine function, this function is often called the signum function ....
.
Generalized error functions
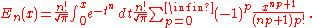
Notable cases are:
- E0(x) is a straight line through the origin:
- E2(x) is the error function, erf(x).
After division by n!, all the En for odd n look similar (but not identical) to each other. Similarly, the En for even n look similar (but not identical) to each other after a simple division by n!. All generalised error functions for n > 0 look similar on the positive x side of the graph.
These generalised functions can equivalently be expressed for x > 0 using the Gamma function
Gamma function
In mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...
and incomplete Gamma function
Incomplete gamma function
In mathematics, the gamma function is defined by a definite integral. The incomplete gamma function is defined as an integral function of the same integrand. There are two varieties of the incomplete gamma function: the upper incomplete gamma function is for the case that the lower limit of...
:
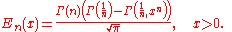
Therefore, we can define the error function in terms of the incomplete Gamma function:
Iterated integrals of the complementary error function
The iterated integrals of the complementary error function are defined by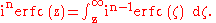
They have the power series
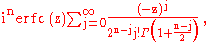
from which follow the symmetry properties
and
Implementations
- C: C99 provides the functions double erf(double x) and double erfc(double x) in the header math.hMath.hC mathematical operations are a group of functions in the standard library of the C programming language implementing basic mathematical functions. Most of the functions involve the use of floating point numbers. Different C standards provide different albeit backwards-compatible, sets of functions...
. The pairs of functions {erff,erfcf} and {erfl,erfcl} take and return values of type float and long double respectively.
- C++: C++11 provides erf and erfc in the header cmath. Both functions are overloaded to accept arguments of type float, double, and long double.
- Fortran: The Fortran 2008 standard provides the ERF, ERFC and ERFC_SCALED functions to calculate the error function and its complement.
- PythonPython (programming language)Python is a general-purpose, high-level programming language whose design philosophy emphasizes code readability. Python claims to "[combine] remarkable power with very clear syntax", and its standard library is large and comprehensive...
: Included since version 2.7 asmath.erf. For previous version, an implementation of erf for complex arguments is in SciPySciPySciPy is an open source library of algorithms and mathematical tools for the Python programming language.SciPy contains modules for optimization, linear algebra, integration, interpolation, special functions, FFT, signal and image processing, ODE solvers and other tasks common in science and...
asscipy.special.erfand also in the arbitrary-precision arithmeticArbitrary-precision arithmeticIn computer science, arbitrary-precision arithmetic indicates that calculations are performed on numbers whose digits of precision are limited only by the available memory of the host system. This contrasts with the faster fixed-precision arithmetic found in most ALU hardware, which typically...
mpmath library asmpmath.erf
- MathematicaMathematicaMathematica is a computational software program used in scientific, engineering, and mathematical fields and other areas of technical computing...
: erf is implemented as Erf and Erfc in Mathematica
- Haskell (programming language)Haskell (programming language)Haskell is a standardized, general-purpose purely functional programming language, with non-strict semantics and strong static typing. It is named after logician Haskell Curry. In Haskell, "a function is a first-class citizen" of the programming language. As a functional programming language, the...
: An erf package exists that provides a typeclass for the error function and implementations for the native floating point types
- RR (programming language)R is a programming language and software environment for statistical computing and graphics. The R language is widely used among statisticians for developing statistical software, and R is widely used for statistical software development and data analysis....
: "The so-called 'error function'" is not provided directly, but is detailed as an example of the normal cumulative distribution function (?pnorm), which is based on W. J. Cody's rational Chebyshev approximation algorithm.
- MatlabMATLABMATLAB is a numerical computing environment and fourth-generation programming language. Developed by MathWorks, MATLAB allows matrix manipulations, plotting of functions and data, implementation of algorithms, creation of user interfaces, and interfacing with programs written in other languages,...
provides both erf and erfc, also via W. J. Cody's algorithm.
- RubyRuby (programming language)Ruby is a dynamic, reflective, general-purpose object-oriented programming language that combines syntax inspired by Perl with Smalltalk-like features. Ruby originated in Japan during the mid-1990s and was first developed and designed by Yukihiro "Matz" Matsumoto...
: ProvidesMath.erfandMath.erfc.
Table of values
| x | erf(x) | erfc(x) | x | erf(x) | erfc(x) | |
|---|---|---|---|---|---|---|
| 0.00 | 0.0000000 | 1.0000000 | 1.30 | 0.9340079 | 0.0659921 | |
| 0.05 | 0.0563720 | 0.9436280 | 1.40 | 0.9522851 | 0.0477149 | |
| 0.10 | 0.1124629 | 0.8875371 | 1.50 | 0.9661051 | 0.0338949 | |
| 0.15 | 0.1679960 | 0.8320040 | 1.60 | 0.9763484 | 0.0236516 | |
| 0.20 | 0.2227026 | 0.7772974 | 1.70 | 0.9837905 | 0.0162095 | |
| 0.25 | 0.2763264 | 0.7236736 | 1.80 | 0.9890905 | 0.0109095 | |
| 0.30 | 0.3286268 | 0.6713732 | 1.90 | 0.9927904 | 0.0072096 | |
| 0.35 | 0.3793821 | 0.6206179 | 2.00 | 0.9953223 | 0.0046777 | |
| 0.40 | 0.4283924 | 0.5716076 | 2.10 | 0.9970205 | 0.0029795 | |
| 0.45 | 0.4754817 | 0.5245183 | 2.20 | 0.9981372 | 0.0018628 | |
| 0.50 | 0.5204999 | 0.4795001 | 2.30 | 0.9988568 | 0.0011432 | |
| 0.55 | 0.5633234 | 0.4366766 | 2.40 | 0.9993115 | 0.0006885 | |
| 0.60 | 0.6038561 | 0.3961439 | 2.50 | 0.9995930 | 0.0004070 | |
| 0.65 | 0.6420293 | 0.3579707 | 2.60 | 0.9997640 | 0.0002360 | |
| 0.70 | 0.6778012 | 0.3221988 | 2.70 | 0.9998657 | 0.0001343 | |
| 0.75 | 0.7111556 | 0.2888444 | 2.80 | 0.9999250 | 0.0000750 | |
| 0.80 | 0.7421010 | 0.2578990 | 2.90 | 0.9999589 | 0.0000411 | |
| 0.85 | 0.7706681 | 0.2293319 | 3.00 | 0.9999779 | 0.0000221 | |
| 0.90 | 0.7969082 | 0.2030918 | 3.10 | 0.9999884 | 0.0000116 | |
| 0.95 | 0.8208908 | 0.1791092 | 3.20 | 0.9999940 | 0.0000060 | |
| 1.00 | 0.8427008 | 0.1572992 | 3.30 | 0.9999969 | 0.0000031 | |
| 1.10 | 0.8802051 | 0.1197949 | 3.40 | 0.9999985 | 0.0000015 | |
| 1.20 | 0.9103140 | 0.0896860 | 3.50 | 0.9999993 | 0.0000007 |
| x | erfc(x)/2 |
|---|---|
| 1 | 0.0786496 |
| 2 | 0.00233887 |
| 3 | 1.10452e-05 |
| 4 | 7.70863e-09 |
| 5 | 7.6873e-13 |
| 6 | 1.07599e-17 |
| 7 | 2.09191e-23 |
| 8 | 5.61215e-30 |
| 9 | 2.06852e-37 |
| 10 | 1.04424e-45 |
| 11 | 7.20433e-55 |
| 12 | 6.78131e-65 |
| 13 | 8.69779e-76 |
| 14 | 1.51861e-87 |
| 15 | 3.6065e-100 |
| 16 | 1.16424e-113 |
| 17 | 5.10614e-128 |
| 18 | 3.04118e-143 |
| 19 | 2.45886e-159 |
| 20 | 2.69793e-176 |
| 21 | 4.01623e-194 |
| 22 | 8.10953e-213 |
| 23 | 2.22063e-232 |
| 24 | 8.24491e-253 |
| 25 | 4.15009e-274 |
| 26 | 2.8316e-296 |
| 27 | 2.61855e-319 |
Related functions
- Gaussian integralGaussian integralThe Gaussian integral, also known as the Euler-Poisson integral or Poisson integral, is the integral of the Gaussian function e−x2 over the entire real line.It is named after the German mathematician and...
, over the whole real line - Gaussian function, derivative
- Dawson function, renormalized imaginary error function
In probability
- Normal distribution
- Normal cumulative distribution function, a scaled and shifted form of error function
- ProbitProbitIn probability theory and statistics, the probit function is the inverse cumulative distribution function , or quantile function associated with the standard normal distribution...
, the inverse or quantile functionQuantile functionIn probability and statistics, the quantile function of the probability distribution of a random variable specifies, for a given probability, the value which the random variable will be at, or below, with that probability...
of the normal CDF - Q-functionQ-functionIn statistics, the Q-function is the tail probability of the standard normal distribution. In other words, Q is the probability that a standard normal random variable will obtain a value larger than x...
, the tail probability of the normal distribution