Indefinite logarithm
Encyclopedia
The indefinite logarithm of a positive number n (variously denoted [log n], Log(n) or even sometimes just log n) is the logarithm without regard to any particular base: it is a function (of the base), not a number. This is as opposed to the ordinary, or definite logarithm
, where there is always (implicitly or explicitly) a particular base to which the logarithm is being taken.
In other words, an indefinite logarithm of a number is a function that is known to have the properties of any logarithm function (i.e., it is defined for all x > 0, log 1 = 0, and log ab = log a + log b), where the base is unknown and the knowledge of the base of the logarithm is unnecessary: it defers the choice of base.
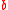. Using lambda calculus
notation, we can express this definition of the Log operator a bit more formally as Log = λ x·(λ b· logb(x)). With this definition, one can easily define addition of indefinite logarithms and their multiplication by scalars, thereby forming a complete
vector space
of indefinite logarithm quantities.
One way to understand the meaning of the indefinite logarithm is to think of it as a dimensioned (i.e., not dimensionless) quantity
. Any such quantity is expressible (in infinitely many ways) as a pair of a (dimensionless) pure number and an arbitrary unit quantity, analogous to the expression of dimensioned physical quantities, such as length, time, or energy (See dimensional analysis
). In the case of the quantities that result from the indefinite logarithm function, their associated units are called logarithmic units. Logarithmic units are themselves indefinite-logarithm quantities, and can be represented with the same notation, e.g.,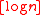
for the logarithmic unit which is equal to the indefinite logarithm of 
.
That is,
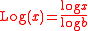
Note that the definite logarithm is an increasing function of the argument x, while the indefinite logarithm is a decreasing function of the base: as the size of units increase, the value of the logarithm for a fixed argument decreases.
Converting a function in two variables into a function of one variable by fixing one of the arguments is known as currying
.
Similarly, given a dimensional quantity such as length, one converts it to a dimensionless number by dividing by a unit: Length(x) = length(x)/length(b): the larger your unit, the smaller your value in those units.
between them, such as, for example, (1 in) / (1 cm) = 2.54. Similarly, two indefinite logarithmic units [log a] and [log b] have a definite numerical ratio between them, given by [log a] / [log b] = logb a. This follows because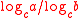
has always the same value, namely 
, regardless of what particular numerical base 
we might choose as the base of our logarithms.
Thus, replacing the indefinite logarithm by a definite logarithm can be compared to representing a length or other physical quantity using a specific unit of measurement. In some contexts, the "unit" for logarithms base 10 are called "bel", abbreviated B and most commonly encountered as decibel
, dB. Similarly, logarithms base 2 are sometimes called "bit
", base 256 "byte
", and base e "neper
".
(with a given consistent choice of base).
We can also define an indefinite exponential, denoted
, which is well-defined (with a pure-number value 
) for indefinite-logarithm quantities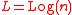 
.
The concepts of indefinite logarithms (and indefinite exponentials) are useful when discussing physical or mathematical quantities that are most naturally defined in terms of logarithms, such as (in particular) information
and entropy
. Such quantities can be considered to be most naturally expressed in terms of indefinite logarithms; that is, they take a value on a logarithmic scale
, though there may not be a natural choice of logarithmic units.
Logarithm
The logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
, where there is always (implicitly or explicitly) a particular base to which the logarithm is being taken.
In other words, an indefinite logarithm of a number is a function that is known to have the properties of any logarithm function (i.e., it is defined for all x > 0, log 1 = 0, and log ab = log a + log b), where the base is unknown and the knowledge of the base of the logarithm is unnecessary: it defers the choice of base.
Definition
The indefinite logarithm operator Log can be defined as the unary operator such that, for any given x > 0, Log(x) returns the entire logarithmic function object b ↦ logb(x), which itself maps any given base b > 0 to the logarithm of x base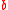. Using lambda calculusLambda calculus
In mathematical logic and computer science, lambda calculus, also written as λ-calculus, is a formal system for function definition, function application and recursion. The portion of lambda calculus relevant to computation is now called the untyped lambda calculus...
notation, we can express this definition of the Log operator a bit more formally as Log = λ x·(λ b· logb(x)). With this definition, one can easily define addition of indefinite logarithms and their multiplication by scalars, thereby forming a complete
Completeness
In general, an object is complete if nothing needs to be added to it. This notion is made more specific in various fields.-Logical completeness:In logic, semantic completeness is the converse of soundness for formal systems...
vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
of indefinite logarithm quantities.
One way to understand the meaning of the indefinite logarithm is to think of it as a dimensioned (i.e., not dimensionless) quantity
Quantity
Quantity is a property that can exist as a magnitude or multitude. Quantities can be compared in terms of "more" or "less" or "equal", or by assigning a numerical value in terms of a unit of measurement. Quantity is among the basic classes of things along with quality, substance, change, and relation...
. Any such quantity is expressible (in infinitely many ways) as a pair of a (dimensionless) pure number and an arbitrary unit quantity, analogous to the expression of dimensioned physical quantities, such as length, time, or energy (See dimensional analysis
Dimensional analysis
In physics and all science, dimensional analysis is a tool to find or check relations among physical quantities by using their dimensions. The dimension of a physical quantity is the combination of the basic physical dimensions which describe it; for example, speed has the dimension length per...
). In the case of the quantities that result from the indefinite logarithm function, their associated units are called logarithmic units. Logarithmic units are themselves indefinite-logarithm quantities, and can be represented with the same notation, e.g.,
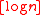for the logarithmic unit which is equal to the indefinite logarithm of .Mathematical details
The logarithm logb x is a function in two variables: the base b and the argument x. If one fixes the base, one obtains the definite logarithm, which is a function of x. If one fixes the number x, one obtains the indefinite logarithm, which is a function of the base b.That is,
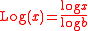
Note that the definite logarithm is an increasing function of the argument x, while the indefinite logarithm is a decreasing function of the base: as the size of units increase, the value of the logarithm for a fixed argument decreases.
Converting a function in two variables into a function of one variable by fixing one of the arguments is known as currying
Currying
In mathematics and computer science, currying is the technique of transforming a function that takes multiple arguments in such a way that it can be called as a chain of functions each with a single argument...
.
Similarly, given a dimensional quantity such as length, one converts it to a dimensionless number by dividing by a unit: Length(x) = length(x)/length(b): the larger your unit, the smaller your value in those units.
In physics
In physics, two units of the same physical dimensions generally have a well-defined numerical ratioRatio
In mathematics, a ratio is a relationship between two numbers of the same kind , usually expressed as "a to b" or a:b, sometimes expressed arithmetically as a dimensionless quotient of the two which explicitly indicates how many times the first number contains the second In mathematics, a ratio is...
between them, such as, for example, (1 in) / (1 cm) = 2.54. Similarly, two indefinite logarithmic units [log a] and [log b] have a definite numerical ratio between them, given by [log a] / [log b] = logb a. This follows because
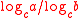has always the same value, namely , regardless of what particular numerical base we might choose as the base of our logarithms.Thus, replacing the indefinite logarithm by a definite logarithm can be compared to representing a length or other physical quantity using a specific unit of measurement. In some contexts, the "unit" for logarithms base 10 are called "bel", abbreviated B and most commonly encountered as decibel
Decibel
The decibel is a logarithmic unit that indicates the ratio of a physical quantity relative to a specified or implied reference level. A ratio in decibels is ten times the logarithm to base 10 of the ratio of two power quantities...
, dB. Similarly, logarithms base 2 are sometimes called "bit
Bit
A bit is the basic unit of information in computing and telecommunications; it is the amount of information stored by a digital device or other physical system that exists in one of two possible distinct states...
", base 256 "byte
Byte
The byte is a unit of digital information in computing and telecommunications that most commonly consists of eight bits. Historically, a byte was the number of bits used to encode a single character of text in a computer and for this reason it is the basic addressable element in many computer...
", and base e "neper
Neper
The neper is a logarithmic unit for ratios of measurements of physical field and power quantities, such as gain and loss of electronic signals. It has the unit symbol Np. The unit's name is derived from the name of John Napier, the inventor of logarithms...
".
In general
In general, the same identities hold for indefinite logarithms as hold for ordinary logarithmsLogarithm
The logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
(with a given consistent choice of base).
We can also define an indefinite exponential, denoted
, which is well-defined (with a pure-number value ) for indefinite-logarithm quantities 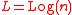.The concepts of indefinite logarithms (and indefinite exponentials) are useful when discussing physical or mathematical quantities that are most naturally defined in terms of logarithms, such as (in particular) information
Information
Information in its most restricted technical sense is a message or collection of messages that consists of an ordered sequence of symbols, or it is the meaning that can be interpreted from such a message or collection of messages. Information can be recorded or transmitted. It can be recorded as...
and entropy
Entropy
Entropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...
. Such quantities can be considered to be most naturally expressed in terms of indefinite logarithms; that is, they take a value on a logarithmic scale
Logarithmic scale
A logarithmic scale is a scale of measurement using the logarithm of a physical quantity instead of the quantity itself.A simple example is a chart whose vertical axis increments are labeled 1, 10, 100, 1000, instead of 1, 2, 3, 4...
, though there may not be a natural choice of logarithmic units.
See also
- LogarithmLogarithmThe logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
- Logarithmic scaleLogarithmic scaleA logarithmic scale is a scale of measurement using the logarithm of a physical quantity instead of the quantity itself.A simple example is a chart whose vertical axis increments are labeled 1, 10, 100, 1000, instead of 1, 2, 3, 4...
- Logarithmic units