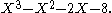In mathematics

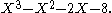
Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, a monogenic field is an algebraic number field

Algebraic number field

In mathematics, an algebraic number field F is a finite field extension of the field of rational numbers Q...

 K for which there exists an element a such that the ring of integers

Ring of integers

In mathematics, the ring of integers is the set of integers making an algebraic structure Z with the operations of integer addition, negation, and multiplication...

 O_K is the polynomial ring Z[a]. The powers of such an element a constitute a power integral basis.

In a monogenic field K, the field discriminant

Discriminant of an algebraic number field

In mathematics, the discriminant of an algebraic number field is a numerical invariant that, loosely speaking, measures the size of the algebraic number field...

 of K is equal to the discriminant

Discriminant

In algebra, the discriminant of a polynomial is an expression which gives information about the nature of the polynomial's roots. For example, the discriminant of the quadratic polynomialax^2+bx+c\,is\Delta = \,b^2-4ac....

 of the minimal polynomial

Minimal polynomial (field theory)

In field theory, given a field extension E / F and an element α of E that is an algebraic element over F, the minimal polynomial of α is the monic polynomial p, with coefficients in F, of least degree such that p = 0...

 of α.

Examples

Examples of monogenic fields include:

• Quadratic fields:

if with a square-free integer

Square-free integer

In mathematics, a square-free, or quadratfrei, integer is one divisible by no perfect square, except 1. For example, 10 is square-free but 18 is not, as it is divisible by 9 = 32...

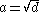, then where if d≡1 (mod 4) and if d ≡ 2 or 3 (mod 4).

• Cyclotomic fields:

if 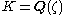with 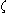a root of unity

Root of unity

In mathematics, a root of unity, or de Moivre number, is any complex number that equals 1 when raised to some integer power n. Roots of unity are used in many branches of mathematics, and are especially important in number theory, the theory of group characters, field theory, and the discrete...

, then

Not all number fields are monogenic; Richard Dedekind

Richard Dedekind

Julius Wilhelm Richard Dedekind was a German mathematician who did important work in abstract algebra , algebraic number theory and the foundations of the real numbers.-Life:...

 gave the example of the cubic field

Cubic field

In mathematics, specifically the area of algebraic number theory, a cubic field is an algebraic number field of degree three.-Definition:If K is a field extension of the rational numbers Q of degree [K:Q] = 3, then K is called a cubic field...

generated by a root of the polynomial