
Dedekind zeta function
Encyclopedia
In mathematics
, the Dedekind zeta function of an algebraic number field
K, generally denoted ζK(s), is a generalization of the Riemann zeta function—which is obtained by specializing to the case where K is the rational number
s Q. In particular, it can be defined as a Dirichlet series, it has an Euler product
expansion, it satisfies a functional equation
, it has an analytic continuation
to a meromorphic function
on the complex plane
C with only a simple pole at s = 1, and its values encode arithmetic data of K. The extended Riemann hypothesis states that if ζK(s) = 0 and 0 < Re(s) < 1, then Re(s) = 1/2.
The Dedekind zeta function is named for Richard Dedekind
who introduced them in his supplement to P.G.L. Dirichlet
's Vorlesungen über Zahlentheorie
.
K. Its Dedekind zeta function is first defined for complex numbers s with real part Re(s) > 1 by the Dirichlet series
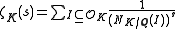
where I ranges through the non-zero ideals
of the ring of integers
OK of K and NK/Q(I) denotes the absolute norm of I (which is equal to both the index
[OK : I] of I in OK or equivalently the cardinality of quotient ring
OK / I). This sum converges absolutely for all complex numbers s with real part Re(s) > 1. In the case K = Q, this definition reduces to that of the Riemann zeta function.
s P of OK
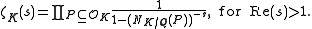
This is the expression in analytic terms of the uniqueness of prime factorization of the ideals
I in OK. The fact that, for Re(s) > 1, ζK(s) is given by a product of non-zero numbers implies that it is non-zero in this region.
first proved that ζK(s) has an analytic continuation to the complex plane as a meromorphic function, having a simple pole only at s = 1. The residue
at that pole is given by the analytic class number formula and is made up of important arithmetic data involving invariants of the unit group and class group of K.
The Dedekind zeta function satisfies a functional equation relating its values at s and 1 − s. Specifically, let ΔK denote discriminant
of K, let r1 (resp. r2) denote the number of real places (resp. complex places) of K, and let
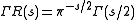
and
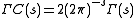
where Γ(s) is the Gamma function
. Then, the function
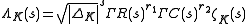
satisfies the functional equation
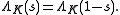
of the unit group of OK and the leading term is given by
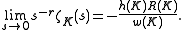
Combining the functional equation and the fact that Γ(s) is zero at all integers less than or equal to zero yields that ζK(s) vanishes at all negative even integers. It even vanishes at all negative odd integers unless K is totally real
(i.e. r2 = 0; e.g. Q or a real quadratic field). In the totally real case, Carl Ludwig Siegel
showed that ζK(s) is a non-zero rational number at negative odd integers. Stephen Lichtenbaum conjectured specific values for these rational numbers in terms of the algebraic K-theory
of K.
of Q, its Dedekind zeta function can be written as a product of Dirichlet L-functions. For example, when K is a quadratic field
this shows that the ratio
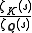
is the L-function L(s, χ), where χ is a Jacobi symbol
as Dirichlet character
. That the zeta function of a quadratic field is a product of the Riemann zeta function and a certain Dirichlet L-function is an analytic formulation of the quadratic reciprocity
law of Gauss.
In general, if K is a Galois extension
of Q with Galois group
G, its Dedekind zeta function is the Artin L-function
of the regular representation
of G and hence has a factorization in terms of Artin L-functions of irreducible Artin representations of G.
Additionally, ζK(s) is the Hasse–Weil zeta function of Spec
OK and the motivic L-function
of the motive
coming from the cohomology
of Spec K.
s to give some examples of pairs of non-isomorphic fields that are arithmetically equivalent. In particular some of these pairs have different class numbers, so the Dedekind zeta function of a number field does not determine its class number.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Dedekind zeta function of an algebraic number field
Algebraic number field
In mathematics, an algebraic number field F is a finite field extension of the field of rational numbers Q...
K, generally denoted ζK(s), is a generalization of the Riemann zeta function—which is obtained by specializing to the case where K is the rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s Q. In particular, it can be defined as a Dirichlet series, it has an Euler product
Euler product
In number theory, an Euler product is an expansion of a Dirichlet series into an infinite product indexed by prime numbers. The name arose from the case of the Riemann zeta-function, where such a product representation was proved by Leonhard Euler.-Definition:...
expansion, it satisfies a functional equation
Functional equation (L-function)
In mathematics, the L-functions of number theory are expected to have several characteristic properties, one of which is that they satisfy certain functional equations. There is an elaborate theory of what these equations should be, much of which is still conjectural...
, it has an analytic continuation
Analytic continuation
In complex analysis, a branch of mathematics, analytic continuation is a technique to extend the domain of a given analytic function. Analytic continuation often succeeds in defining further values of a function, for example in a new region where an infinite series representation in terms of which...
to a meromorphic function
Meromorphic function
In complex analysis, a meromorphic function on an open subset D of the complex plane is a function that is holomorphic on all D except a set of isolated points, which are poles for the function...
on the complex plane
Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
C with only a simple pole at s = 1, and its values encode arithmetic data of K. The extended Riemann hypothesis states that if ζK(s) = 0 and 0 < Re(s) < 1, then Re(s) = 1/2.
The Dedekind zeta function is named for Richard Dedekind
Richard Dedekind
Julius Wilhelm Richard Dedekind was a German mathematician who did important work in abstract algebra , algebraic number theory and the foundations of the real numbers.-Life:...
who introduced them in his supplement to P.G.L. Dirichlet
Johann Peter Gustav Lejeune Dirichlet
Johann Peter Gustav Lejeune Dirichlet was a German mathematician with deep contributions to number theory , as well as to the theory of Fourier series and other topics in mathematical analysis; he is credited with being one of the first mathematicians to give the modern formal definition of a...
's Vorlesungen über Zahlentheorie
Vorlesungen über Zahlentheorie
' is a textbook of number theory written by German mathematicians Lejeune Dirichlet and Richard Dedekind, and published in 1863....
.
Definition and basic properties
Let K be an algebraic number fieldAlgebraic number field
In mathematics, an algebraic number field F is a finite field extension of the field of rational numbers Q...
K. Its Dedekind zeta function is first defined for complex numbers s with real part Re(s) > 1 by the Dirichlet series
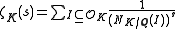
where I ranges through the non-zero ideals
Ideal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
of the ring of integers
Ring of integers
In mathematics, the ring of integers is the set of integers making an algebraic structure Z with the operations of integer addition, negation, and multiplication...
OK of K and NK/Q(I) denotes the absolute norm of I (which is equal to both the index
Index of a subgroup
In mathematics, specifically group theory, the index of a subgroup H in a group G is the "relative size" of H in G: equivalently, the number of "copies" of H that fill up G. For example, if H has index 2 in G, then intuitively "half" of the elements of G lie in H...
[OK : I] of I in OK or equivalently the cardinality of quotient ring
Quotient ring
In ring theory, a branch of modern algebra, a quotient ring, also known as factor ring or residue class ring, is a construction quite similar to the factor groups of group theory and the quotient spaces of linear algebra...
OK / I). This sum converges absolutely for all complex numbers s with real part Re(s) > 1. In the case K = Q, this definition reduces to that of the Riemann zeta function.
Euler product
The Dedekind zeta function of K has an Euler product which is a product over all the prime idealPrime ideal
In algebra , a prime ideal is a subset of a ring which shares many important properties of a prime number in the ring of integers...
s P of OK
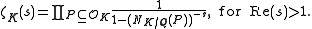
This is the expression in analytic terms of the uniqueness of prime factorization of the ideals
Dedekind domain
In abstract algebra, a Dedekind domain or Dedekind ring, named after Richard Dedekind, is an integral domain in which every nonzero proper ideal factors into a product of prime ideals. It can be shown that such a factorization is then necessarily unique up to the order of the factors...
I in OK. The fact that, for Re(s) > 1, ζK(s) is given by a product of non-zero numbers implies that it is non-zero in this region.
Analytic continuation and functional equation
Erich HeckeErich Hecke
Erich Hecke was a German mathematician. He obtained his doctorate in Göttingen under the supervision of David Hilbert. Kurt Reidemeister and Heinrich Behnke were among his students....
first proved that ζK(s) has an analytic continuation to the complex plane as a meromorphic function, having a simple pole only at s = 1. The residue
Residue (complex analysis)
In mathematics, more specifically complex analysis, the residue is a complex number proportional to the contour integral of a meromorphic function along a path enclosing one of its singularities...
at that pole is given by the analytic class number formula and is made up of important arithmetic data involving invariants of the unit group and class group of K.
The Dedekind zeta function satisfies a functional equation relating its values at s and 1 − s. Specifically, let ΔK denote discriminant
Discriminant of an algebraic number field
In mathematics, the discriminant of an algebraic number field is a numerical invariant that, loosely speaking, measures the size of the algebraic number field...
of K, let r1 (resp. r2) denote the number of real places (resp. complex places) of K, and let
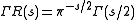
and
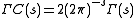
where Γ(s) is the Gamma function
Gamma function
In mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...
. Then, the function
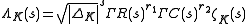
satisfies the functional equation
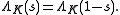
Special values
Analogously to the Riemann zeta function, the values of the Dedekind zeta function at integers encode (at least conjecturally) important arithmetic data of the field K. For example, the analytic class number formula relates the residue at s = 1 to the class number h(K) of K, the regulator R(K) of K, the number w(K) of roots of unity in K, the absolute discriminant of K, and the number of real and complex places of K. Another example is at s = 0 where it has a zero whose order r is equal to the rankRank of an abelian group
In mathematics, the rank, Prüfer rank, or torsion-free rank of an abelian group A is the cardinality of a maximal linearly independent subset. The rank of A determines the size of the largest free abelian group contained in A. If A is torsion-free then it embeds into a vector space over the...
of the unit group of OK and the leading term is given by
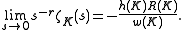
Combining the functional equation and the fact that Γ(s) is zero at all integers less than or equal to zero yields that ζK(s) vanishes at all negative even integers. It even vanishes at all negative odd integers unless K is totally real
Totally real number field
In number theory, a number field K is called totally real if for each embedding of K into the complex numbers the image lies inside the real numbers...
(i.e. r2 = 0; e.g. Q or a real quadratic field). In the totally real case, Carl Ludwig Siegel
Carl Ludwig Siegel
Carl Ludwig Siegel was a mathematician specialising in number theory and celestial mechanics. He was one of the most important mathematicians of the 20th century.-Biography:...
showed that ζK(s) is a non-zero rational number at negative odd integers. Stephen Lichtenbaum conjectured specific values for these rational numbers in terms of the algebraic K-theory
Algebraic K-theory
In mathematics, algebraic K-theory is an important part of homological algebra concerned with defining and applying a sequenceof functors from rings to abelian groups, for all integers n....
of K.
Relations to other L-functions
For the case in which K is an abelian extensionAbelian extension
In abstract algebra, an abelian extension is a Galois extension whose Galois group is abelian. When the Galois group is a cyclic group, we have a cyclic extension. More generally, a Galois extension is called solvable if its Galois group is solvable....
of Q, its Dedekind zeta function can be written as a product of Dirichlet L-functions. For example, when K is a quadratic field
Quadratic field
In algebraic number theory, a quadratic field is an algebraic number field K of degree two over Q. It is easy to show that the map d ↦ Q is a bijection from the set of all square-free integers d ≠ 0, 1 to the set of all quadratic fields...
this shows that the ratio
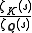
is the L-function L(s, χ), where χ is a Jacobi symbol
Jacobi symbol
The Jacobi symbol is a generalization of the Legendre symbol. Introduced by Jacobi in 1837, it is of theoretical interest in modular arithmetic and other branches of number theory, but its main use is in computational number theory, especially primality testing and integer factorization; these in...
as Dirichlet character
Dirichlet character
In number theory, Dirichlet characters are certain arithmetic functions which arise from completely multiplicative characters on the units of \mathbb Z / k \mathbb Z...
. That the zeta function of a quadratic field is a product of the Riemann zeta function and a certain Dirichlet L-function is an analytic formulation of the quadratic reciprocity
Quadratic reciprocity
In number theory, the law of quadratic reciprocity is a theorem about modular arithmetic which gives conditions for the solvability of quadratic equations modulo prime numbers...
law of Gauss.
In general, if K is a Galois extension
Galois extension
In mathematics, a Galois extension is an algebraic field extension E/F satisfying certain conditions ; one also says that the extension is Galois. The significance of being a Galois extension is that the extension has a Galois group and obeys the fundamental theorem of Galois theory.The definition...
of Q with Galois group
Galois group
In mathematics, more specifically in the area of modern algebra known as Galois theory, the Galois group of a certain type of field extension is a specific group associated with the field extension...
G, its Dedekind zeta function is the Artin L-function
Artin L-function
In mathematics, an Artin L-function is a type of Dirichlet series associated to a linear representation ρ of a Galois group G. These functions were introduced in the 1923 by Emil Artin, in connection with his research into class field theory. Their fundamental properties, in particular the Artin...
of the regular representation
Regular representation
In mathematics, and in particular the theory of group representations, the regular representation of a group G is the linear representation afforded by the group action of G on itself by translation....
of G and hence has a factorization in terms of Artin L-functions of irreducible Artin representations of G.
Additionally, ζK(s) is the Hasse–Weil zeta function of Spec
Spectrum of a ring
In abstract algebra and algebraic geometry, the spectrum of a commutative ring R, denoted by Spec, is the set of all proper prime ideals of R...
OK and the motivic L-function
Motivic L-function
In mathematics, motivic L-functions are a generalization of Hasse–Weil L-functions to general motives over global fields. The local L-factor at a finite place v is similarly given by the characteristic polynomial of a Frobenius element at v acting on the v-inertial invariants of the v-adic...
of the motive
Motive (algebraic geometry)
In algebraic geometry, a motive denotes 'some essential part of an algebraic variety'. To date, pure motives have been defined, while conjectural mixed motives have not. Pure motives are triples , where X is a smooth projective variety, p : X ⊢ X is an idempotent correspondence, and m an integer...
coming from the cohomology
Cohomology
In mathematics, specifically in algebraic topology, cohomology is a general term for a sequence of abelian groups defined from a co-chain complex. That is, cohomology is defined as the abstract study of cochains, cocycles, and coboundaries...
of Spec K.
Arithmetically equivalent fields
Two fields are called arithmetically equivalent if they have the same Dedekind zeta function. used Gassmann tripleGassmann triple
In mathematics, a Gassmann triple is a group G together with two faithful actions on sets X and Y, such that X and Y are not isomorphic as G-sets but every element of G has the same number of fixed points on X and Y...
s to give some examples of pairs of non-isomorphic fields that are arithmetically equivalent. In particular some of these pairs have different class numbers, so the Dedekind zeta function of a number field does not determine its class number.

