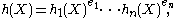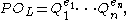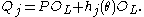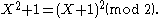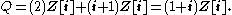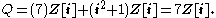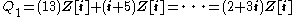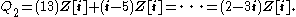Splitting of prime ideals in Galois extensions
Encyclopedia
In mathematics
, the interplay between the Galois group
G of a Galois extension
L of a number field K, and the way the prime ideal
s P of the ring of integers
OK factorise as products of prime ideals of OL, provides one of the richest parts of algebraic number theory
. The splitting of prime ideals in Galois extensions is sometimes attributed to David Hilbert
by calling it Hilbert theory. There is a geometric analogue, for ramified coverings of Riemann surface
s, which is simpler in that only one kind of subgroup of G need be considered, rather than two. This was certainly familiar before Hilbert.
of L and K, respectively, which are defined to be the integral closure of the integers Z in the field in question. Finally, let p be a non-zero prime ideal in A, or equivalently, a maximal ideal
, so that the residue A/p is a field
.
From the basic theory of one-dimensional
rings follows the existence of a unique decomposition
of the ideal pB generated in B by p into a product of distinct maximal ideals Pj, with multiplicities e(j).
The multiplicity e(j) are called ramification indices of the extension at p. If they are all equal to 1 and if in addition the field extensions B/Pj over A/p is separable
, the field extension L/K is called unramified at p.
If this is the case, by the Chinese remainder theorem
, the quotient
. Then the Galois group
G acts transitively on the Pj. That is, the prime ideal factors of P in L form a single orbit under the automorphism
s of L over K. From this and the unicity of prime factorisation, it follows that e(j) = e is independent of j; something that certainly need not be the case for extensions that are not Galois.
The basic relation then reads
In the geometric analogue, for complex manifold
s or algebraic geometry
over an algebraically closed field
, the concepts of decomposition group and inertia group coincide. There, given a Galois ramified cover, all but finitely many points have the same number of preimages.
The splitting of primes in extensions that are not Galois may be studied by using a splitting field
initially, i.e. a Galois extension that is somewhat larger. For example cubic field
s usually are 'regulated' by a degree 6 field containing them.
Writing G for the Galois group of Q(i)/Q, and σ for the complex conjugation automorphism in G, there are three cases to consider.
so the ramification index here is e = 2. The residue field is
which is the finite field with two elements. The decomposition group must be equal to all of G, since there is only one prime of Z[i] above 2. The inertia group is also all of G, since
modulo (1+i), for any integers a and b.
In fact, 2 is the only prime that ramifies in Z[i], since every prime that ramifies must divide the discriminant
of Z[i], which is −4.
The decomposition groups in this case are both the trivial group {1}; indeed the automorphism σ switches the two primes (2 + 3i) and (2 − 3i), so it cannot be in the decomposition group of either prime. The inertia group, being a subgroup of the decomposition group, is also the trivial group. There are two residue fields, one for each prime,
which are both isomorphic to the finite field with 13 elements. The Frobenius element is the trivial automorphism; this means that
modulo (2 ± 3i), for any integers a and b.
which is the finite field with 72 = 49 elements. For example, the difference between 1 + i and σ(1 + i) = 1 − i is 2i, which is certainly not divisible by 7. Therefore the inertia group is the trivial group {1}. The Galois group of this residue field over the subfield Z/7Z has order 2, and is generated by the image of the Frobenius element. The Frobenius is none other than σ; this means that
modulo 7, for any integers a and b.
The following procedure (Neukirch, p47) solves this problem in many cases. The strategy is to select an integer θ in OL so that L is generated over K by θ (such a θ is guaranteed to exist by the primitive element theorem
), and then to examine the minimal polynomial
H(X) of θ over K; it is a monic polynomial with coefficients in OK. Reducing the coefficients of H(X) modulo P, we obtain a monic polynomial h(X) with coefficients in F, the (finite) residue field OK/P. Suppose that h(X) factorises in the polynomial ring F[X] as
where the hj are distinct monic irreducible polynomials in F[X]. Then, as long as P is not one of finitely many exceptional primes (the precise condition is described below), the factorisation of P has the following form:
where the Qj are distinct prime ideals of OL. Furthermore, the inertia degree of each Qj is equal to the degree of the corresponding polynomial hj, and there is an explicit formula for the Qj:
In the Galois case, the inertia degrees are all equal, and the ramification indices e1 = ... = en are all equal.
The exceptional primes, for which the above result does not necessarily hold, are the ones not relatively prime to the conductor of the ring OK[θ]. The conductor is defined to be the ideal
it measures how far the order OK[θ] is from being the whole ring of integers (maximal order) OL.
A significant caveat is that there exist examples of L/K and P such that there is no available θ that satisfies the above hypotheses (see for example ). Therefore the algorithm given above cannot be used to factor such P, and more sophisticated approaches must be used, such as that described in.
 ] is the whole ring of integers of Q(
] is the whole ring of integers of Q( ), the conductor is the unit ideal, so there are no exceptional primes.
), the conductor is the unit ideal, so there are no exceptional primes.
For P = (2), we need to work in the field Z/(2)Z, which amounts to factorising the polynomial X2 + 1 modulo 2:
Therefore there is only one prime factor, with inertia degree 1 and ramification index 2, and it is given by
The next case is for P = (p) for a prime p ≡ 3 mod 4. For concreteness we will take P = (7). The polynomial X2 + 1 is irreducible modulo 7. Therefore there is only one prime factor, with inertia degree 2 and ramification index 1, and it is given by
The last case is P = (p) for a prime p ≡ 1 mod 4; we will again take P = (13). This time we have the factorisation
Therefore there are two prime factors, both with inertia degree and ramification index 1. They are given by
and
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the interplay between the Galois group
Galois group
In mathematics, more specifically in the area of modern algebra known as Galois theory, the Galois group of a certain type of field extension is a specific group associated with the field extension...
G of a Galois extension
Galois extension
In mathematics, a Galois extension is an algebraic field extension E/F satisfying certain conditions ; one also says that the extension is Galois. The significance of being a Galois extension is that the extension has a Galois group and obeys the fundamental theorem of Galois theory.The definition...
L of a number field K, and the way the prime ideal
Prime ideal
In algebra , a prime ideal is a subset of a ring which shares many important properties of a prime number in the ring of integers...
s P of the ring of integers
Ring of integers
In mathematics, the ring of integers is the set of integers making an algebraic structure Z with the operations of integer addition, negation, and multiplication...
OK factorise as products of prime ideals of OL, provides one of the richest parts of algebraic number theory
Algebraic number theory
Algebraic number theory is a major branch of number theory which studies algebraic structures related to algebraic integers. This is generally accomplished by considering a ring of algebraic integers O in an algebraic number field K/Q, and studying their algebraic properties such as factorization,...
. The splitting of prime ideals in Galois extensions is sometimes attributed to David Hilbert
David Hilbert
David Hilbert was a German mathematician. He is recognized as one of the most influential and universal mathematicians of the 19th and early 20th centuries. Hilbert discovered and developed a broad range of fundamental ideas in many areas, including invariant theory and the axiomatization of...
by calling it Hilbert theory. There is a geometric analogue, for ramified coverings of Riemann surface
Riemann surface
In mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...
s, which is simpler in that only one kind of subgroup of G need be considered, rather than two. This was certainly familiar before Hilbert.
Definitions
Let L / K be a finite extension of number fields, and let B and A be the corresponding ring of integersRing of integers
In mathematics, the ring of integers is the set of integers making an algebraic structure Z with the operations of integer addition, negation, and multiplication...
of L and K, respectively, which are defined to be the integral closure of the integers Z in the field in question. Finally, let p be a non-zero prime ideal in A, or equivalently, a maximal ideal
Maximal ideal
In mathematics, more specifically in ring theory, a maximal ideal is an ideal which is maximal amongst all proper ideals. In other words, I is a maximal ideal of a ring R if I is an ideal of R, I ≠ R, and whenever J is another ideal containing I as a subset, then either J = I or J = R...
, so that the residue A/p is a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
.
From the basic theory of one-dimensional
Krull dimension
In commutative algebra, the Krull dimension of a ring R, named after Wolfgang Krull , is the supremum of the number of strict inclusions in a chain of prime ideals. The Krull dimension need not be finite even for a Noetherian ring....
rings follows the existence of a unique decomposition
- pB = Π Pje(j)
of the ideal pB generated in B by p into a product of distinct maximal ideals Pj, with multiplicities e(j).
The multiplicity e(j) are called ramification indices of the extension at p. If they are all equal to 1 and if in addition the field extensions B/Pj over A/p is separable
Separable extension
In modern algebra, an algebraic field extension E\supseteq F is a separable extension if and only if for every \alpha\in E, the minimal polynomial of \alpha over F is a separable polynomial . Otherwise, the extension is called inseparable...
, the field extension L/K is called unramified at p.
If this is the case, by the Chinese remainder theorem
Chinese remainder theorem
The Chinese remainder theorem is a result about congruences in number theory and its generalizations in abstract algebra.In its most basic form it concerned with determining n, given the remainders generated by division of n by several numbers...
, the quotient
-
- B/pB
- is a product of fields
- Fj = B/Pj.
The Galois situation
In the following, the extension L / K is assumed to be a Galois extensionGalois extension
In mathematics, a Galois extension is an algebraic field extension E/F satisfying certain conditions ; one also says that the extension is Galois. The significance of being a Galois extension is that the extension has a Galois group and obeys the fundamental theorem of Galois theory.The definition...
. Then the Galois group
Galois group
In mathematics, more specifically in the area of modern algebra known as Galois theory, the Galois group of a certain type of field extension is a specific group associated with the field extension...
G acts transitively on the Pj. That is, the prime ideal factors of P in L form a single orbit under the automorphism
Automorphism
In mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism...
s of L over K. From this and the unicity of prime factorisation, it follows that e(j) = e is independent of j; something that certainly need not be the case for extensions that are not Galois.
The basic relation then reads
- pB = (Π Pj)e
Facts
- Given an extension as above, it is unramified in all but finitely many points.
- In the unramified case, because of the transitivity of the Galois group action, the fields Fj introduced above are all isomorphic, say to the finite field F′, containing
-
- F = A/p
- A counting argument shows that
- [L:K]/[F′:F]
- equals the number of prime factors of P in B. By the orbit-stabilizer formula this number is also equal to
- |G|/|D|
- where by definition D, the decomposition group of p, is the subgroup of elements of G sending a given Pj to itself. That is, since the degree of L/K and the order of G are equal by basic Galois theory, the order of the decomposition group D is the degree of the residue field extension F′/F. The theory of the Frobenius element goes further, to identify an element of D, for j given, which generates the Galois group of the finite field extension.
- In the ramified case, there is the further phenomenon of inertia: the index e is interpreted as the extent to which elements of G are not seen in the Galois groups of any of the residue field extensions. Each decomposition group D, for a given Pj, contains an inertia group I consisting of the g in G that send Pj to itself, but induce the identity automorphism on
-
- Fj = B/Pj.
In the geometric analogue, for complex manifold
Complex manifold
In differential geometry, a complex manifold is a manifold with an atlas of charts to the open unit disk in Cn, such that the transition maps are holomorphic....
s or algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
over an algebraically closed field
Algebraically closed field
In mathematics, a field F is said to be algebraically closed if every polynomial with one variable of degree at least 1, with coefficients in F, has a root in F.-Examples:...
, the concepts of decomposition group and inertia group coincide. There, given a Galois ramified cover, all but finitely many points have the same number of preimages.
The splitting of primes in extensions that are not Galois may be studied by using a splitting field
Splitting field
In abstract algebra, a splitting field of a polynomial with coefficients in a field is a smallest field extension of that field over which the polynomial factors into linear factors.-Definition:...
initially, i.e. a Galois extension that is somewhat larger. For example cubic field
Cubic field
In mathematics, specifically the area of algebraic number theory, a cubic field is an algebraic number field of degree three.-Definition:If K is a field extension of the rational numbers Q of degree [K:Q] = 3, then K is called a cubic field...
s usually are 'regulated' by a degree 6 field containing them.
Example — the Gaussian integers
This section describes the splitting of prime ideals in the field extension Q(i)/Q. That is, we take K = Q and L = Q(i), so OK is simply Z, and OL = Z[i] is the ring of Gaussian integers. Although this case is far from representative — after all, Z[i] has unique factorisation — it exhibits many of the features of the theory.Writing G for the Galois group of Q(i)/Q, and σ for the complex conjugation automorphism in G, there are three cases to consider.
The prime p = 2
The prime 2 of Z ramifies in Z[i]:- (2) = (1+i)2,
so the ramification index here is e = 2. The residue field is
- OL / (1+i)OL
which is the finite field with two elements. The decomposition group must be equal to all of G, since there is only one prime of Z[i] above 2. The inertia group is also all of G, since
- a + bi ≡ a − bi
modulo (1+i), for any integers a and b.
In fact, 2 is the only prime that ramifies in Z[i], since every prime that ramifies must divide the discriminant
Discriminant of an algebraic number field
In mathematics, the discriminant of an algebraic number field is a numerical invariant that, loosely speaking, measures the size of the algebraic number field...
of Z[i], which is −4.
Primes p ≡ 1 mod 4
Any prime p ≡ 1 mod 4 splits into two distinct prime ideals in Z[i]; this is a manifestation of Fermat's theorem on sums of two squares. For example,- (13) = (2 + 3i)(2 − 3i).
The decomposition groups in this case are both the trivial group {1}; indeed the automorphism σ switches the two primes (2 + 3i) and (2 − 3i), so it cannot be in the decomposition group of either prime. The inertia group, being a subgroup of the decomposition group, is also the trivial group. There are two residue fields, one for each prime,
- OL / (2 ± 3i)OL,
which are both isomorphic to the finite field with 13 elements. The Frobenius element is the trivial automorphism; this means that
- (a + bi)13 ≡ a + bi
modulo (2 ± 3i), for any integers a and b.
Primes p ≡ 3 mod 4
Any prime p ≡ 3 mod 4 remains inert in Z[i]; that is, it does not split. For example, (7) remains prime in Z[i]. In this situation, the decomposition group is all of G, again because there is only one prime factor. However, this situation differs from the p = 2 case, because now σ does not act trivially on the residue field- OL / (7)OL,
which is the finite field with 72 = 49 elements. For example, the difference between 1 + i and σ(1 + i) = 1 − i is 2i, which is certainly not divisible by 7. Therefore the inertia group is the trivial group {1}. The Galois group of this residue field over the subfield Z/7Z has order 2, and is generated by the image of the Frobenius element. The Frobenius is none other than σ; this means that
- (a + bi)7 ≡ a − bi
modulo 7, for any integers a and b.
Summary
| Prime in Z | How it splits in Z[i] | Inertia group | Decomposition group |
|---|---|---|---|
| 2 | Ramifies with index 2 | G | G |
| p ≡ 1 mod 4 | Splits into two distinct factors | 1 | 1 |
| p ≡ 3 mod 4 | Remains inert | 1 | G |
Computing the factorisation
Suppose that we wish to determine the factorisation of a prime ideal P of OK into primes of OL. We will assume that the extension L/K is a finite separable extension; the extra hypothesis of normality in the definition of Galois extension is not necessary.The following procedure (Neukirch, p47) solves this problem in many cases. The strategy is to select an integer θ in OL so that L is generated over K by θ (such a θ is guaranteed to exist by the primitive element theorem
Primitive element theorem
In mathematics, more specifically in the area of modern algebra known as field theory, the primitive element theorem or Artin's theorem on primitive elements is a result characterizing the finite degree field extensions that possess a primitive element...
), and then to examine the minimal polynomial
Minimal polynomial (field theory)
In field theory, given a field extension E / F and an element α of E that is an algebraic element over F, the minimal polynomial of α is the monic polynomial p, with coefficients in F, of least degree such that p = 0...
H(X) of θ over K; it is a monic polynomial with coefficients in OK. Reducing the coefficients of H(X) modulo P, we obtain a monic polynomial h(X) with coefficients in F, the (finite) residue field OK/P. Suppose that h(X) factorises in the polynomial ring F[X] as
where the hj are distinct monic irreducible polynomials in F[X]. Then, as long as P is not one of finitely many exceptional primes (the precise condition is described below), the factorisation of P has the following form:
where the Qj are distinct prime ideals of OL. Furthermore, the inertia degree of each Qj is equal to the degree of the corresponding polynomial hj, and there is an explicit formula for the Qj:
In the Galois case, the inertia degrees are all equal, and the ramification indices e1 = ... = en are all equal.
The exceptional primes, for which the above result does not necessarily hold, are the ones not relatively prime to the conductor of the ring OK[θ]. The conductor is defined to be the ideal
it measures how far the order OK[θ] is from being the whole ring of integers (maximal order) OL.
A significant caveat is that there exist examples of L/K and P such that there is no available θ that satisfies the above hypotheses (see for example ). Therefore the algorithm given above cannot be used to factor such P, and more sophisticated approaches must be used, such as that described in.
An example
Consider again the case of the Gaussian integers. We take θ to be the imaginary unit i, with minimal polynomial H(X) = X2 + 1. Since Z[ ] is the whole ring of integers of Q(
] is the whole ring of integers of Q( ), the conductor is the unit ideal, so there are no exceptional primes.
), the conductor is the unit ideal, so there are no exceptional primes.For P = (2), we need to work in the field Z/(2)Z, which amounts to factorising the polynomial X2 + 1 modulo 2:
Therefore there is only one prime factor, with inertia degree 1 and ramification index 2, and it is given by
The next case is for P = (p) for a prime p ≡ 3 mod 4. For concreteness we will take P = (7). The polynomial X2 + 1 is irreducible modulo 7. Therefore there is only one prime factor, with inertia degree 2 and ramification index 1, and it is given by
The last case is P = (p) for a prime p ≡ 1 mod 4; we will again take P = (13). This time we have the factorisation
Therefore there are two prime factors, both with inertia degree and ramification index 1. They are given by
and