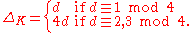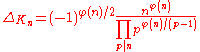Discriminant of an algebraic number field
Encyclopedia
In mathematics
, the discriminant of an algebraic number field
is a numerical invariant
that, loosely speaking, measures the size of the (ring of integers
of the) algebraic number field. More specifically, it is related to the volume of the fundamental domain
of the ring of integers, and it regulates which primes
are ramified.
The discriminant is one of the most basic invariants of a number field, and occurs in several important analytic
formulas such as the functional equation
of the Dedekind zeta function
of K, and the analytic class number formula for K. An old theorem of Hermite
states that there are only finitely many number fields of bounded discriminant, however determining this quantity is still an open problem
, and the subject of current research.
The discriminant of K can be referred to as the absolute discriminant of K to distinguish it from the relative discriminant of an extension
K/L of number fields. The latter is an ideal
in the ring of integers of L, and like the absolute discriminant it indicates which primes are ramified in K/L. It is a generalization of the absolute discriminant allowing for L to be bigger than Q; in fact, when L = Q, the relative discriminant of K/Q is the principal ideal
of Z generated by the absolute discriminant of K.
), and let {σ1, ..., σn} be the set of embeddings of K into the complex number
s (i.e. ring homomorphism
s K → C). The discriminant of K is the square of the determinant
of the n by n matrix
B whose (i,j)-entry is σi(bj). Symbolically,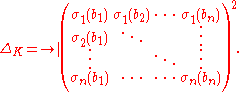
Equivalently, the trace
from K to Q can be used. Specifically, define the trace form to be the matrix whose (i,j)-entry is
TrK/Q(bibj). This matrix equals BTB, so the discriminant of K is the determinant of this matrix.
 The definition of the discriminant of a general algebraic number field, K, was given by Dedekind in 1871. At this point, he already knew the relationship between the discriminant and ramification.
The definition of the discriminant of a general algebraic number field, K, was given by Dedekind in 1871. At this point, he already knew the relationship between the discriminant and ramification.
Hermite's theorem predates the general definition of the discriminant with Charles Hermite publishing a proof of it in 1857. In 1877, Alexander von Brill
determined the sign of the discriminant. Leopold Kronecker
first stated Minkowski's theorem in 1882, though the first proof was given by Hermann Minkowski in 1891. In the same year, Minkowski published his bound on the discriminant. Near the end of the nineteenth century, Ludwig Stickelberger
obtained his theorem on the residue of the discriminant modulo four.
of K/L. When L = Q, the relative discriminant ΔK/Q is the principal ideal of Z generated by the absolute discriminant ΔK . In a tower of fields K/L/F the relative discriminants are related by
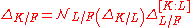
where denotes relative norm
denotes relative norm
.
is a non-trivial unramified extension.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the discriminant of an algebraic number field
Algebraic number field
In mathematics, an algebraic number field F is a finite field extension of the field of rational numbers Q...
is a numerical invariant
Invariant (mathematics)
In mathematics, an invariant is a property of a class of mathematical objects that remains unchanged when transformations of a certain type are applied to the objects. The particular class of objects and type of transformations are usually indicated by the context in which the term is used...
that, loosely speaking, measures the size of the (ring of integers
Ring of integers
In mathematics, the ring of integers is the set of integers making an algebraic structure Z with the operations of integer addition, negation, and multiplication...
of the) algebraic number field. More specifically, it is related to the volume of the fundamental domain
Fundamental domain
In geometry, the fundamental domain of a symmetry group of an object is a part or pattern, as small or irredundant as possible, which determines the whole object based on the symmetry. More rigorously, given a topological space and a group acting on it, the images of a single point under the group...
of the ring of integers, and it regulates which primes
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
are ramified.
The discriminant is one of the most basic invariants of a number field, and occurs in several important analytic
Analytic number theory
In mathematics, analytic number theory is a branch of number theory that uses methods from mathematical analysis to solve problems about the integers. It is often said to have begun with Dirichlet's introduction of Dirichlet L-functions to give the first proof of Dirichlet's theorem on arithmetic...
formulas such as the functional equation
Functional equation (L-function)
In mathematics, the L-functions of number theory are expected to have several characteristic properties, one of which is that they satisfy certain functional equations. There is an elaborate theory of what these equations should be, much of which is still conjectural...
of the Dedekind zeta function
Dedekind zeta function
In mathematics, the Dedekind zeta function of an algebraic number field K, generally denoted ζK, is a generalization of the Riemann zeta function—which is obtained by specializing to the case where K is the rational numbers Q...
of K, and the analytic class number formula for K. An old theorem of Hermite
Charles Hermite
Charles Hermite was a French mathematician who did research on number theory, quadratic forms, invariant theory, orthogonal polynomials, elliptic functions, and algebra....
states that there are only finitely many number fields of bounded discriminant, however determining this quantity is still an open problem
Open problem
In science and mathematics, an open problem or an open question is a known problem that can be accurately stated, and has not yet been solved . Some questions remain unanswered for centuries before solutions are found...
, and the subject of current research.
The discriminant of K can be referred to as the absolute discriminant of K to distinguish it from the relative discriminant of an extension
Field extension
In abstract algebra, field extensions are the main object of study in field theory. The general idea is to start with a base field and construct in some manner a larger field which contains the base field and satisfies additional properties...
K/L of number fields. The latter is an ideal
Ideal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
in the ring of integers of L, and like the absolute discriminant it indicates which primes are ramified in K/L. It is a generalization of the absolute discriminant allowing for L to be bigger than Q; in fact, when L = Q, the relative discriminant of K/Q is the principal ideal
Principal ideal
In ring theory, a branch of abstract algebra, a principal ideal is an ideal I in a ring R that is generated by a single element a of R.More specifically:...
of Z generated by the absolute discriminant of K.
Definition
Let K be an algebraic number field, and let OK be its ring of integers. Let b1, ..., bn be an integral basis of OK (i.e. a basis as a Z-moduleModule (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
), and let {σ1, ..., σn} be the set of embeddings of K into the complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s (i.e. ring homomorphism
Ring homomorphism
In ring theory or abstract algebra, a ring homomorphism is a function between two rings which respects the operations of addition and multiplication....
s K → C). The discriminant of K is the square of the determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
of the n by n matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
B whose (i,j)-entry is σi(bj). Symbolically,
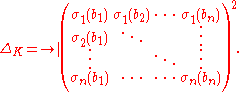
Equivalently, the trace
Field trace
In mathematics, the field trace is a function defined with respect to a finite field extension L/K. It is a K-linear map from L to K...
from K to Q can be used. Specifically, define the trace form to be the matrix whose (i,j)-entry is
TrK/Q(bibj). This matrix equals BTB, so the discriminant of K is the determinant of this matrix.
Examples
- Quadratic number fields: let d be a square-free integerSquare-free integerIn mathematics, a square-free, or quadratfrei, integer is one divisible by no perfect square, except 1. For example, 10 is square-free but 18 is not, as it is divisible by 9 = 32...
, then the discriminant of is
is
-
-
- An integer that occurs as the discriminant of a quadratic number field is called a fundamental discriminantFundamental discriminantIn mathematics, a fundamental discriminant D is an integer invariant in the theory of integral binary quadratic forms. If is a quadratic form with integer coefficients, then is the discriminant of Q. Conversely, every integer D with is the discriminant of some binary quadratic form with integer...
.- Cyclotomic fieldCyclotomic fieldIn number theory, a cyclotomic field is a number field obtained by adjoining a complex primitive root of unity to Q, the field of rational numbers...
s: let n > 2 be an integer, let ζn be a primitive nth root of unityRoot of unityIn mathematics, a root of unity, or de Moivre number, is any complex number that equals 1 when raised to some integer power n. Roots of unity are used in many branches of mathematics, and are especially important in number theory, the theory of group characters, field theory, and the discrete...
, and let Kn = Q(ζn) be the nth cyclotomic field. The discriminant of Kn is given by
- Cyclotomic field
- where
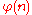 is Euler's totient functionEuler's totient functionIn number theory, the totient \varphi of a positive integer n is defined to be the number of positive integers less than or equal to n that are coprime to n In number theory, the totient \varphi(n) of a positive integer n is defined to be the number of positive integers less than or equal to n that...
is Euler's totient functionEuler's totient functionIn number theory, the totient \varphi of a positive integer n is defined to be the number of positive integers less than or equal to n that are coprime to n In number theory, the totient \varphi(n) of a positive integer n is defined to be the number of positive integers less than or equal to n that...
, and the product in the denominator is over primes p dividing n.- Power bases: In the case where the ring of integers has a power integral basis, that is, can be written as OK = Z[α], the discriminant of K is equal to the discriminantDiscriminantIn algebra, the discriminant of a polynomial is an expression which gives information about the nature of the polynomial's roots. For example, the discriminant of the quadratic polynomialax^2+bx+c\,is\Delta = \,b^2-4ac....
of the minimal polynomialMinimal polynomial (field theory)In field theory, given a field extension E / F and an element α of E that is an algebraic element over F, the minimal polynomial of α is the monic polynomial p, with coefficients in F, of least degree such that p = 0...
of α. To see this, one can chose the integral basis of OK to be b1 = 1, b2 = α, b3 = α2, ..., bn = αn−1. Then, the matrix in the definition is the Vandermonde matrix associated to αi = σi(α), whose determinant squared is
- Power bases: In the case where the ring of integers has a power integral basis, that is, can be written as OK = Z[α], the discriminant of K is equal to the discriminant
- which is exactly the definition of the discriminant of the minimal polynomial.
- Let K = Q(α) be the number field obtained by adjoiningAdjunction (field theory)In abstract algebra, adjunction is a construction in field theory, where for a given field extension E/F, subextensions between E and F are constructed.- Definition :...
a root α of the polynomialPolynomialIn mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
x3 − x2 − 2x − 8. This is Richard DedekindRichard DedekindJulius Wilhelm Richard Dedekind was a German mathematician who did important work in abstract algebra , algebraic number theory and the foundations of the real numbers.-Life:...
's original example of a number field whose ring of integers does not possess a power basis. An integral basis is given by {1, α, α(α + 1)/2} and the discriminant of K is −503. - Repeated discriminants: the discriminant of a quadratic field uniquely identifies it, but this is not true, in general, for higher-degree number fields. For example, there are two non-isomorphicIsomorphismIn abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
cubic fieldCubic fieldIn mathematics, specifically the area of algebraic number theory, a cubic field is an algebraic number field of degree three.-Definition:If K is a field extension of the rational numbers Q of degree [K:Q] = 3, then K is called a cubic field...
s of discriminant 3969. They are obtained by adjoining a root of the polynomial or , respectively.
- Let K = Q(α) be the number field obtained by adjoining
Basic results
- The signSign (mathematics)In mathematics, the word sign refers to the property of being positive or negative. Every nonzero real number is either positive or negative, and therefore has a sign. Zero itself is signless, although in some contexts it makes sense to consider a signed zero...
of the discriminant is (−1)r2 where r2 is the number of complex places of K. - A prime p ramifies in K if, and only if, p divides ΔK .
- Stickelberger's Theorem:
-
-
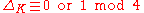
- MinkowskiHermann MinkowskiHermann Minkowski was a German mathematician of Ashkenazi Jewish descent, who created and developed the geometry of numbers and who used geometrical methods to solve difficult problems in number theory, mathematical physics, and the theory of relativity.- Life and work :Hermann Minkowski was born...
bound: Let n denote the degreeDegree of a field extensionIn mathematics, more specifically field theory, the degree of a field extension is a rough measure of the "size" of the extension. The concept plays an important role in many parts of mathematics, including algebra and number theory — indeed in any area where fields appear prominently.-...
of the extension K/Q and r2 the number of complex places of K, then
- Minkowski
-
 .
.
-
- Minkowski's Theorem: If K is not Q, then |ΔK| > 1 (this follows directly from the Minkowski bound).
- Hermite's Theorem: Let N be a positive integer. There are only finitely many algebraic number fields K with ΔK < N.
History

Hermite's theorem predates the general definition of the discriminant with Charles Hermite publishing a proof of it in 1857. In 1877, Alexander von Brill
Alexander von Brill
Alexander Wilhelm von Brill was a German mathematician.Born in Darmstadt, Hesse, he attended University of Giessen where he earned his doctorate under supervision of Alfred Clebsch. He held a chair at the University of Tübingen, where Max Planck was among his students.-External links:...
determined the sign of the discriminant. Leopold Kronecker
Leopold Kronecker
Leopold Kronecker was a German mathematician who worked on number theory and algebra.He criticized Cantor's work on set theory, and was quoted by as having said, "God made integers; all else is the work of man"...
first stated Minkowski's theorem in 1882, though the first proof was given by Hermann Minkowski in 1891. In the same year, Minkowski published his bound on the discriminant. Near the end of the nineteenth century, Ludwig Stickelberger
Ludwig Stickelberger
Ludwig Stickelberger was a Swiss mathematician who made important contributions to linear algebra and algebraic number theory .-Short biography:Stickelberger was born in Buch in the canton of Schaffhausen into a family of a...
obtained his theorem on the residue of the discriminant modulo four.
Relative discriminant
The discriminant defined above is sometimes referred to as the absolute discriminant of K to distinguish it from the relative discriminant ΔK/L of an extension of number fields K/L, which is an ideal in OL. The relative discriminant is defined in a fashion similar to the absolute discriminant, but must take into account that ideals in OL may not be principal and that there may not be an integral basis of K/L. Let {σ1, ..., σn} be the set of embeddings of K into C which are the identity on L. If b1, ..., bn is any basis of K over L, let d(b1, ..., bn) be the square of the determinant of the n by n matrix whose (i,j)-entry is σi(bj). Then, the relative discriminant of K/L is the ideal generated by the d(b1, ..., bn) as {b1, ..., bn} varies over all bases of K/L with the property that bi ∈ OK for all i. Alternatively, the relative discriminant of K/L is the norm of the differentDifferent ideal
In algebraic number theory, the different ideal is defined to account for the lack of duality in the ring of integers of an algebraic number field K, with respect to the field trace...
of K/L. When L = Q, the relative discriminant ΔK/Q is the principal ideal of Z generated by the absolute discriminant ΔK . In a tower of fields K/L/F the relative discriminants are related by
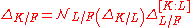
where
 denotes relative norm
denotes relative normField norm
In mathematics, the norm is a mapping defined in field theory, to map elements of a larger field into a smaller one.-Formal definitions:1. Let K be a field and L a finite extension of K...
.
Ramification
The relative discriminant regulates the ramification data of the field extension K/L. A prime ideal p of L ramifies in K if, and only if, it divides the relative discriminant ΔK/L. An extension is unramified if, and only if, the discriminant is the unit ideal. The Minkowski bound above shows that there are no non-trivial unramified extensions of Q. Fields larger than Q may have unramified extensions, for example, for any field with class number greater than one, its Hilbert class fieldHilbert class field
In algebraic number theory, the Hilbert class field E of a number field K is the maximal abelian unramified extension of K. Its degree over K equals the class number of K and the Galois group of E over K is canonically isomorphic to the ideal class group of K using Frobenius elements for prime...
is a non-trivial unramified extension.
Root discriminant
The root discriminant of a number field, K, of degree n, often denoted rdK, is defined as the n-th root of the absolute value of the (absolute) discriminant of K. The relation between relative discriminants in a tower of fields shows that the root discriminant does not change in an unramified extension.Relation to other quantities
- When embedded into
 , the volume of the fundamental domain of OK is
, the volume of the fundamental domain of OK is 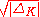 (sometimes a different measureMeasure (mathematics)In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
(sometimes a different measureMeasure (mathematics)In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
is used and the volume obtained is , where r2 is the number of complex places of K).
, where r2 is the number of complex places of K). - Due to its appearance in this volume, the discriminant also appears in the functional equation of the Dedekind zeta function of K, and hence in the analytic class number formula, and the Brauer-Siegel theoremBrauer-Siegel theoremIn mathematics, the Brauer–Siegel theorem, named after Richard Brauer and Carl Ludwig Siegel, is an asymptotic result on the behaviour of algebraic number fields, obtained by Richard Brauer and Carl Ludwig Siegel...
. - The relative discriminant of K/L is the Artin conductor of the regular representationRegular representationIn mathematics, and in particular the theory of group representations, the regular representation of a group G is the linear representation afforded by the group action of G on itself by translation....
of the Galois groupGalois groupIn mathematics, more specifically in the area of modern algebra known as Galois theory, the Galois group of a certain type of field extension is a specific group associated with the field extension...
of K/L. This provides a relation to the Artin conductors of the charactersCharacter groupIn mathematics, a character group is the group of representations of a group by complex-valued functions. These functions can be thought of as one-dimensional matrix representations and so are special cases of the group characters which arises in the related context of character theory...
of the Galois group of K/L, called the conductor-discriminant formula.