
Eisenstein integer
Encyclopedia
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Eisenstein integers (named after Gotthold Eisenstein), also known as Eulerian integers (after Leonhard Euler
Leonhard Euler
Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
), are complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s of the form
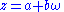
where a and b are integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s and
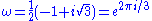
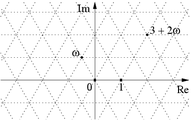
is a primitive (non-real) cube root of unity. The Eisenstein integers form a triangular lattice in the complex plane
Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
, in contrast with the Gaussian integers which form a square lattice in the complex plane.
Properties
The Eisenstein integers form a commutative ringCommutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
of algebraic integer
Algebraic integer
In number theory, an algebraic integer is a complex number that is a root of some monic polynomial with coefficients in . The set of all algebraic integers is closed under addition and multiplication and therefore is a subring of complex numbers denoted by A...
s in the algebraic number field
Algebraic number field
In mathematics, an algebraic number field F is a finite field extension of the field of rational numbers Q...
Q(ω). To see that the Eisenstein integers are algebraic integers note that each z = a + bω is a root of the monic polynomial
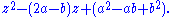
In particular, ω satisfies the equation

The norm of a Eisenstein integer is just the square of its absolute value
Absolute value
In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
and is given by
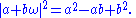
Thus the norm of an Eisenstein integer is always an ordinary (rational) integer. Since
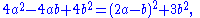
the norm of a nonzero Eisenstein integer is positive.
The group of units in the ring of Eisenstein integers is the cyclic group
Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
formed by the sixth roots of unity in the complex plane. Specifically, they are
- {±1, ±ω, ±ω2}
These are just the Eisenstein integers of norm one.
Eisenstein primes
If x and y are Eisenstein integers, we say that x divides y if there is some Eisenstein integer z such that y = z x.This extends the notion of divisibility for ordinary integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s. Therefore we may also extend the notion of primality; a non-unit Eisenstein integer x is said to be an Eisenstein prime
Eisenstein prime
In mathematics, an Eisenstein prime is an Eisenstein integerz = a + b\,\omega\qquadthat is irreducible in the ring-theoretic sense: its only Eisenstein divisors are the units , a + bω itself and its associates.The associates and the complex conjugate...
if its only divisors are of the form ux where u is any of the six units.
It may be shown that an ordinary prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
(or rational prime) which is 3 or congruent to 1 mod 3 is of the form x2 − xy + y2 for some integers x, y and may therefore be factored into (x + ωy)(x + ω2y) and because of that it is not prime in the Eisenstein integers. Ordinary primes congruent to 2 mod 3 cannot be factored in this way and they are primes in the Eisenstein integers as well.
Every Eisenstein integer a + bω whose norm a2 − ab + b2 is a rational prime is an Eisenstein prime. In fact, every Eisenstein prime is of this form, or is a product of a unit and a rational prime congruent to 2 mod 3.
Euclidean domain
The ring of Eisenstein integers forms a Euclidean domainEuclidean domain
In mathematics, more specifically in abstract algebra and ring theory, a Euclidean domain is a ring that can be endowed with a certain structure – namely a Euclidean function, to be described in detail below – which allows a suitable generalization of the Euclidean algorithm...
whose norm N is given by

This can be derived as follows:
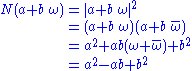
Quotient of C by the Eisenstein integers
The quotient of the complex plane C by the latticeLattice (group)
In mathematics, especially in geometry and group theory, a lattice in Rn is a discrete subgroup of Rn which spans the real vector space Rn. Every lattice in Rn can be generated from a basis for the vector space by forming all linear combinations with integer coefficients...
containing all Eisenstein integers is a complex torus
Complex torus
In mathematics, a complex torus is a particular kind of complex manifold M whose underlying smooth manifold is a torus in the usual sense...
of real dimension 2, with the highest degree of symmetry
Symmetry
Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...
among all such complex tori.
See also
- Gaussian integerGaussian integerIn number theory, a Gaussian integer is a complex number whose real and imaginary part are both integers. The Gaussian integers, with ordinary addition and multiplication of complex numbers, form an integral domain, usually written as Z[i]. The Gaussian integers are a special case of the quadratic...
- Kummer ring
- Systolic geometry
- Hermite constant
- Cubic reciprocityCubic reciprocityCubic reciprocity is a collection of theorems in elementary and algebraic number theory that state conditions under which the congruence x3 ≡ p is solvable; the word "reciprocity" comes from the form of the main theorem, which states that if p and q are primary numbers in the...
- Loewner's torus inequalityLoewner's torus inequalityIn differential geometry, Loewner's torus inequality is an inequality due to Charles Loewner. It relates the systole and the area of an arbitrary Riemannian metric on the 2-torus.-Statement:...
- Hurwitz quaternionHurwitz quaternionIn mathematics, a Hurwitz quaternion is a quaternion whose components are either all integers or all half-integers...
- Quadratic integerQuadratic integerIn number theory, quadratic integers are a generalization of the rational integers to quadratic fields. Important examples include the Gaussian integers and the Eisenstein integers. Though they have been studied for more than a hundred years, many open problems remain.- Definition :Quadratic...

