
Absolute value (algebra)
Encyclopedia
In mathematics
, an absolute value is a function
which measures the "size" of elements in a field
or integral domain. More precisely, if D is an integral domain, then an absolute value is any mapping | x | from D to the real numbers R satisfying:
From the second and third of these it can be seen that | 1 | = 1 and | −1 | = 1. Furthermore, for any positive integer n,
Note that some authors use the terms valuation, norm or magnitude instead of "absolute value".
Every integral domain has at least one absolute value, called the trivial value. This is the absolute value with | x | = 0 when x = 0 and | x | = 1 otherwise. The trivial value is the only possible absolute value on a finite field.
Ostrowski's theorem
states that the nontrivial places of the rational numbers Q are the ordinary absolute value
and the p-adic absolute value
for each prime p. For a given prime p, the p-adic absolute value of the rational number q = pn(a/b), where a and b are integers not divisible by p, is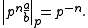
Since the ordinary absolute value and the p-adic absolute values are normalized, these define places.
Such a function is known as a valuation in the terminology of Bourbaki, but other authors use the term valuation for absolute value and then say exponential valuation instead of valuation.
s of elements of D with respect to the absolute value by requiring that for every r > 0 there is a positive integer N such that for all integers m, n > N one has | xm − xn | < r. It is not hard to show that Cauchy sequences under pointwise addition and multiplication form a ring
. One can also define null sequences as sequences of elements of D such that | an | converges to zero. Null sequences are a prime ideal
in the ring of Cauchy sequences, and the quotient ring
is therefore an integral domain. The domain D is embedded
in this quotient ring, called the completion of D with respect to the absolute value | x |.
Since fields are integral domains, this is also a construction for the completion of a field with respect to an absolute value. To show that the result is a field, and not just an integral domain, we can either show that null sequences form a maximal ideal
, or else construct the inverse directly. The latter can be easily done by taking, for all nonzero elements of the quotient ring, a sequence starting from a point beyond the last zero element of the sequence. Any nonzero element of the quotient ring will differ by a null sequence from such a sequence, and by taking pointwise inversion we can find a representative inverse element.
Another theorem of Alexander Ostrowski
has it that any field complete with respect to the usual Archimedean
absolute value is isomorphic to either the real or the complex numbers. Ultrametric complete fields are far more numerous, however.
The Gelfand-Tornheim theorem states that any field with an Archimedean valuation is isomorphic to a subfield of C, the valuation being equivalent to the usual absolute value on C.
of D by setting
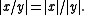
On the other hand, if F is a field with ultrametric absolute value | x |, then the set of elements of F such that | x | ≤ 1 defines a valuation ring
, which is a subring D of F such that for every nonzero element x of F, at least one of x or x−1 belongs to D. Since F is a field, D has no zero divisors and is an integral domain. It has a unique maximal ideal
consisting of all x such that | x | < 1, and is therefore a local ring
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, an absolute value is a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
which measures the "size" of elements in a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
or integral domain. More precisely, if D is an integral domain, then an absolute value is any mapping | x | from D to the real numbers R satisfying:
- | x | ≥ 0,
- | x | = 0 if and only if x = 0,
- | xy | = | x || y |,
- | x + y | ≤ | x | + | y |.
From the second and third of these it can be seen that | 1 | = 1 and | −1 | = 1. Furthermore, for any positive integer n,
- | 1+1+...(n times) | = | −1−1...(n times) | ≤ n.
Note that some authors use the terms valuation, norm or magnitude instead of "absolute value".
Types of absolute value
If | x + y | satisfies the stronger property | x + y | ≤ max(|x|, |y|), then | x | is called an ultrametric or non-Archimedean absolute value, and otherwise an Archimedean absolute value.Every integral domain has at least one absolute value, called the trivial value. This is the absolute value with | x | = 0 when x = 0 and | x | = 1 otherwise. The trivial value is the only possible absolute value on a finite field.
Places
If | x |1 and | x |2 are two absolute values on the same integral domain D, then the two absolute values are equivalent if | x |1 < 1 if and only if | x |2 < 1. If two nontrivial absolute values are equivalent, then for some exponent e, we have | x |1e = | x |2. (Note that we cannot necessarily raise one absolute value to some power and obtain another. For instance, squaring the usual absolute value on the real numbers yields a function which is not an absolute value.) Absolute values up to equivalence, or in other words, an equivalence class of absolute values, is called a place.Ostrowski's theorem
Ostrowski's theorem
Ostrowski's theorem, due to Alexander Ostrowski , states that any non-trivial absolute value on the rational numbers Q is equivalent to either the usual real absolute value or a p-adic absolute value.- Definitions :...
states that the nontrivial places of the rational numbers Q are the ordinary absolute value
Absolute value
In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
and the p-adic absolute value
P-adic number
In mathematics, and chiefly number theory, the p-adic number system for any prime number p extends the ordinary arithmetic of the rational numbers in a way different from the extension of the rational number system to the real and complex number systems...
for each prime p. For a given prime p, the p-adic absolute value of the rational number q = pn(a/b), where a and b are integers not divisible by p, is
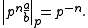
Since the ordinary absolute value and the p-adic absolute values are normalized, these define places.
Valuations
If for some ultrametric absolute value we define ν(x) = -logb| x | for any base b > 1, and extend by defining ν(0) = ∞, which is ordered to be greater than all real numbers, we obtain a function from D to R ∪ {∞}, with the following properties:- ν(x) = ∞ ⇒ x = 0,
- ν(xy) = ν(x) + ν(y),
- ν(x + y) ≥ min(ν(x), ν(y)).
Such a function is known as a valuation in the terminology of Bourbaki, but other authors use the term valuation for absolute value and then say exponential valuation instead of valuation.
Completions
Given an integral domain D with an absolute value, we can define the Cauchy sequenceCauchy sequence
In mathematics, a Cauchy sequence , named after Augustin-Louis Cauchy, is a sequence whose elements become arbitrarily close to each other as the sequence progresses...
s of elements of D with respect to the absolute value by requiring that for every r > 0 there is a positive integer N such that for all integers m, n > N one has | xm − xn | < r. It is not hard to show that Cauchy sequences under pointwise addition and multiplication form a ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
. One can also define null sequences as sequences of elements of D such that | an | converges to zero. Null sequences are a prime ideal
Prime ideal
In algebra , a prime ideal is a subset of a ring which shares many important properties of a prime number in the ring of integers...
in the ring of Cauchy sequences, and the quotient ring
Quotient ring
In ring theory, a branch of modern algebra, a quotient ring, also known as factor ring or residue class ring, is a construction quite similar to the factor groups of group theory and the quotient spaces of linear algebra...
is therefore an integral domain. The domain D is embedded
Embedding
In mathematics, an embedding is one instance of some mathematical structure contained within another instance, such as a group that is a subgroup....
in this quotient ring, called the completion of D with respect to the absolute value | x |.
Since fields are integral domains, this is also a construction for the completion of a field with respect to an absolute value. To show that the result is a field, and not just an integral domain, we can either show that null sequences form a maximal ideal
Maximal ideal
In mathematics, more specifically in ring theory, a maximal ideal is an ideal which is maximal amongst all proper ideals. In other words, I is a maximal ideal of a ring R if I is an ideal of R, I ≠ R, and whenever J is another ideal containing I as a subset, then either J = I or J = R...
, or else construct the inverse directly. The latter can be easily done by taking, for all nonzero elements of the quotient ring, a sequence starting from a point beyond the last zero element of the sequence. Any nonzero element of the quotient ring will differ by a null sequence from such a sequence, and by taking pointwise inversion we can find a representative inverse element.
Another theorem of Alexander Ostrowski
Alexander Ostrowski
Alexander Markowich Ostrowski , was a mathematician.His father Mark having been a merchant, Alexander Ostrowski attended the Kiev College of Commerce, not a high school, and thus had an insufficient qualification to be admitted to university...
has it that any field complete with respect to the usual Archimedean
Archimedean
Archimedean means of or pertaining to or named in honor of the Greek mathematician Archimedes. These are most commonly:* Archimedean property* Archimedean absolute value* Archimedean solid* Archimedean point* Archimedean tiling* Archimedean spiral...
absolute value is isomorphic to either the real or the complex numbers. Ultrametric complete fields are far more numerous, however.
The Gelfand-Tornheim theorem states that any field with an Archimedean valuation is isomorphic to a subfield of C, the valuation being equivalent to the usual absolute value on C.
Fields and integral domains
If D is an integral domain with absolute value | x |, then we may extend the definition of the absolute value to the field of fractionsField of fractions
In abstract algebra, the field of fractions or field of quotients of an integral domain is the smallest field in which it can be embedded. The elements of the field of fractions of the integral domain R have the form a/b with a and b in R and b ≠ 0...
of D by setting
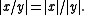
On the other hand, if F is a field with ultrametric absolute value | x |, then the set of elements of F such that | x | ≤ 1 defines a valuation ring
Valuation ring
In abstract algebra, a valuation ring is an integral domain D such that for every element x of its field of fractions F, at least one of x or x −1 belongs to D....
, which is a subring D of F such that for every nonzero element x of F, at least one of x or x−1 belongs to D. Since F is a field, D has no zero divisors and is an integral domain. It has a unique maximal ideal
Maximal ideal
In mathematics, more specifically in ring theory, a maximal ideal is an ideal which is maximal amongst all proper ideals. In other words, I is a maximal ideal of a ring R if I is an ideal of R, I ≠ R, and whenever J is another ideal containing I as a subset, then either J = I or J = R...
consisting of all x such that | x | < 1, and is therefore a local ring
Local ring
In abstract algebra, more particularly in ring theory, local rings are certain rings that are comparatively simple, and serve to describe what is called "local behaviour", in the sense of functions defined on varieties or manifolds, or of algebraic number fields examined at a particular place, or...
.

