
Adele ring
Encyclopedia
In algebraic number theory
and topological algebra
, the adele ring is a topological ring
which is built on the field
of rational number
s (or, more generally, any algebraic number field
). It involves all the completions of the field.
The word "adele" is short for "additive idele". The ring of adeles was historically preceded (before 1950) by what was known as the ring of repartitions, a construction which avoids completions, and is today sometimes referred to as pre-adele.
of the rings Z/nZ:
By the Chinese remainder theorem
it is isomorphic to the product of all the rings of p-adic integers:
The ring of integral adeles AZ is the product
The ring of (rational) adeles AQ is the tensor product

(topologized so that AZ is an open subring).
More generally the ring of adeles AF of any algebraic number field F is the tensor product
(topologized as the product of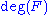 copies of AQ).
copies of AQ).
The ring of (rational) adeles can also be defined as the restricted product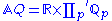
of all the p-adic completions
Qp and the real number
s (or in other words as the restricted product of all completions of the rationals). In this case the restricted product means that for an adele (a∞, a2, a3, a5, …) all but a finite number of the ap are p-adic integers.
The adeles of a function field
over a finite field can be defined in a similar way, as the restricted product of all completions.
with the rational numbers Q contained as a discrete co-compact subgroup. The use of adele rings in connection with Fourier transform
s was exploited in Tate's thesis
(1950). One key property of the additive group of adeles is that it is topologically and algebraically isomorphic to its Pontryagin dual; in other words it is a self-dual space. Its self-duality underlies the functional equation for the zeta function of a global field
.
, often as the coefficients in matrix group
s: that is, combined with the theory of algebraic group
s to construct adelic algebraic group
s. The idele group of class field theory
appears as the group of 1×1 invertible matrices over the adeles. (It is not given the subset topology, as the inverse is not continuous in this topology. Instead the ideles are identified with the closed subset of all pairs (x,y) of A×A
with xy=1, with the subset topology.)
An important stage in the development of the theory was the definition of the Tamagawa number for an adelic linear algebraic group. This is a volume measure relating G(Q) with G(A), saying how G(Q), which is a discrete group
in G(A), lies in the latter. A conjecture of André Weil
was that the Tamagawa number was always 1 for a simply connected G. This arose out of Weil's modern treatment of results in the theory of quadratic form
s; the proof was case-by-case and took decades. The final steps were taken by Robert Kottwitz in 1988 and V.I. Chernousov in 1989.
Meanwhile the influence of the Tamagawa number idea was felt in the theory of abelian varieties. There the application by no means works, in any straightforward way. But during the formulation of the Birch and Swinnerton-Dyer conjecture
, the consideration that for an elliptic curve
E the group of rational points E(Q) might be brought into relation with the E(Qp) was one motivation and a signpost on the way from numerical evidence to the conjecture.
Algebraic number theory
Algebraic number theory is a major branch of number theory which studies algebraic structures related to algebraic integers. This is generally accomplished by considering a ring of algebraic integers O in an algebraic number field K/Q, and studying their algebraic properties such as factorization,...
and topological algebra
Topological algebra
In mathematics, a topological algebra A over a topological field K is a topological vector space together with a continuous multiplication\cdot :A\times A \longrightarrow A\longmapsto a\cdot bthat makes it an algebra over K...
, the adele ring is a topological ring
Topological ring
In mathematics, a topological ring is a ring R which is also a topological space such that both the addition and the multiplication are continuous as mapswhere R × R carries the product topology.- General comments :...
which is built on the field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
of rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s (or, more generally, any algebraic number field
Algebraic number field
In mathematics, an algebraic number field F is a finite field extension of the field of rational numbers Q...
). It involves all the completions of the field.
The word "adele" is short for "additive idele". The ring of adeles was historically preceded (before 1950) by what was known as the ring of repartitions, a construction which avoids completions, and is today sometimes referred to as pre-adele.
Definitions
The profinite completion of the integers, Ẑ, is the inverse limitInverse limit
In mathematics, the inverse limit is a construction which allows one to "glue together" several related objects, the precise manner of the gluing process being specified by morphisms between the objects...
of the rings Z/nZ:

By the Chinese remainder theorem
Chinese remainder theorem
The Chinese remainder theorem is a result about congruences in number theory and its generalizations in abstract algebra.In its most basic form it concerned with determining n, given the remainders generated by division of n by several numbers...
it is isomorphic to the product of all the rings of p-adic integers:

The ring of integral adeles AZ is the product

The ring of (rational) adeles AQ is the tensor product
Tensor product of algebras
In mathematics, the tensor product of two R-algebras is also an R-algebra. This gives us a tensor product of algebras. The special case R = Z gives us a tensor product of rings, since rings may be regarded as Z-algebras....

(topologized so that AZ is an open subring).
More generally the ring of adeles AF of any algebraic number field F is the tensor product

(topologized as the product of
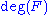 copies of AQ).
copies of AQ).The ring of (rational) adeles can also be defined as the restricted product
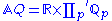
of all the p-adic completions
P-adic number
In mathematics, and chiefly number theory, the p-adic number system for any prime number p extends the ordinary arithmetic of the rational numbers in a way different from the extension of the rational number system to the real and complex number systems...
Qp and the real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s (or in other words as the restricted product of all completions of the rationals). In this case the restricted product means that for an adele (a∞, a2, a3, a5, …) all but a finite number of the ap are p-adic integers.
The adeles of a function field
Function field of an algebraic variety
In algebraic geometry, the function field of an algebraic variety V consists of objects which are interpreted as rational functions on V...
over a finite field can be defined in a similar way, as the restricted product of all completions.
Properties
The rational adeles A are a locally compact groupGroup (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
with the rational numbers Q contained as a discrete co-compact subgroup. The use of adele rings in connection with Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
s was exploited in Tate's thesis
Tate's thesis
In number theory, Tate's thesis is the thesis of where he reformulated the work of Erich Hecke on L-series in terms of Fourier analysis on adelic groups....
(1950). One key property of the additive group of adeles is that it is topologically and algebraically isomorphic to its Pontryagin dual; in other words it is a self-dual space. Its self-duality underlies the functional equation for the zeta function of a global field
Global field
In mathematics, the term global field refers to either of the following:*an algebraic number field, i.e., a finite extension of Q, or*a global function field, i.e., the function field of an algebraic curve over a finite field, equivalently, a finite extension of Fq, the field of rational functions...
.
Applications
The ring A is much used in advanced parts of number theoryNumber theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, often as the coefficients in matrix group
Matrix group
In mathematics, a matrix group is a group G consisting of invertible matrices over some field K, usually fixed in advance, with operations of matrix multiplication and inversion. More generally, one can consider n × n matrices over a commutative ring R...
s: that is, combined with the theory of algebraic group
Algebraic group
In algebraic geometry, an algebraic group is a group that is an algebraic variety, such that the multiplication and inverse are given by regular functions on the variety...
s to construct adelic algebraic group
Adelic algebraic group
In abstract algebra, an adelic algebraic group is a topological group defined by an algebraic group G over a number field K, and the adele ring A = A of K. It consists of the points of G having values in A; the definition of the appropriate topology is straightforward only in case G is a linear...
s. The idele group of class field theory
Class field theory
In mathematics, class field theory is a major branch of algebraic number theory that studies abelian extensions of number fields.Most of the central results in this area were proved in the period between 1900 and 1950...
appears as the group of 1×1 invertible matrices over the adeles. (It is not given the subset topology, as the inverse is not continuous in this topology. Instead the ideles are identified with the closed subset of all pairs (x,y) of A×A
with xy=1, with the subset topology.)
An important stage in the development of the theory was the definition of the Tamagawa number for an adelic linear algebraic group. This is a volume measure relating G(Q) with G(A), saying how G(Q), which is a discrete group
Discrete group
In mathematics, a discrete group is a group G equipped with the discrete topology. With this topology G becomes a topological group. A discrete subgroup of a topological group G is a subgroup H whose relative topology is the discrete one...
in G(A), lies in the latter. A conjecture of André Weil
Weil conjecture on Tamagawa numbers
In mathematics, the Weil conjecture on Tamagawa numbers is a result about algebraic groups formulated by André Weil in the late 1950s and proved in 1989...
was that the Tamagawa number was always 1 for a simply connected G. This arose out of Weil's modern treatment of results in the theory of quadratic form
Quadratic form
In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....
s; the proof was case-by-case and took decades. The final steps were taken by Robert Kottwitz in 1988 and V.I. Chernousov in 1989.
Meanwhile the influence of the Tamagawa number idea was felt in the theory of abelian varieties. There the application by no means works, in any straightforward way. But during the formulation of the Birch and Swinnerton-Dyer conjecture
Birch and Swinnerton-Dyer conjecture
In mathematics, the Birch and Swinnerton-Dyer conjecture is an open problem in the field of number theory. Its status as one of the most challenging mathematical questions has become widely recognized; the conjecture was chosen as one of the seven Millennium Prize Problems listed by the Clay...
, the consideration that for an elliptic curve
Elliptic curve
In mathematics, an elliptic curve is a smooth, projective algebraic curve of genus one, on which there is a specified point O. An elliptic curve is in fact an abelian variety — that is, it has a multiplication defined algebraically with respect to which it is a group — and O serves as the identity...
E the group of rational points E(Q) might be brought into relation with the E(Qp) was one motivation and a signpost on the way from numerical evidence to the conjecture.

