
Integrally closed
Encyclopedia
In mathematics
, more specifically in abstract algebra
, the concept of integrally closed has two meanings, one for groups
and one for rings
.
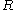 contained in a ring
contained in a ring 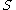 is said to be integrally closed in
is said to be integrally closed in 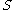 if
if  is equal to the integral closure of
is equal to the integral closure of 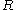 in
in 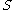 . That is, for every monic polynomial f with coefficients in
. That is, for every monic polynomial f with coefficients in 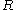 , every root of f belonging to S also belongs to
, every root of f belonging to S also belongs to 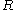 . Typically if one refers to a domain being integrally closed without reference to an overring
. Typically if one refers to a domain being integrally closed without reference to an overring
, it is meant that the ring is integrally closed in its field of fractions
, the largest overring of the domain.
If the ring is not a domain, typically being integrally closed means that every local ring
is an integrally closed domain.
Sometimes a domain that is integrally closed is called "normal" if it is integrally closed and being thought of as a variety.
In this respect, the normalization of a variety
(or scheme
) is simply the of the integral closure of all of the rings.
of the integral closure of all of the rings.
G is called integrally closed if and only if
for all elements a and b of G, if an ≤ b for all natural n then a ≤ 1.
This property is somewhat stronger than the fact that an ordered group is Archimedean
. Though for a lattice-ordered group to be integrally closed and to be Archimedean is equivalent.
We have the surprising theorem that every integrally closed directed
group is already abelian
. This has to do with the fact that a directed group is embeddable into a complete lattice-ordered group if and only if it is integrally closed. Furthermore, every archimedean lattice-ordered group is abelian.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, more specifically in abstract algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, the concept of integrally closed has two meanings, one for groups
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
and one for rings
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
.
Commutative rings
A commutative ring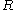 contained in a ring
contained in a ring 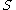 is said to be integrally closed in
is said to be integrally closed in 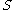 if
if  is equal to the integral closure of
is equal to the integral closure of 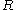 in
in 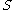 . That is, for every monic polynomial f with coefficients in
. That is, for every monic polynomial f with coefficients in 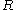 , every root of f belonging to S also belongs to
, every root of f belonging to S also belongs to 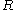 . Typically if one refers to a domain being integrally closed without reference to an overring
. Typically if one refers to a domain being integrally closed without reference to an overringOverring
In mathematics, an overring B of an integral domain A is a subring of the field of fractions K of A that contains A: i.e., A \subseteq B \subseteq K....
, it is meant that the ring is integrally closed in its field of fractions
Field of fractions
In abstract algebra, the field of fractions or field of quotients of an integral domain is the smallest field in which it can be embedded. The elements of the field of fractions of the integral domain R have the form a/b with a and b in R and b ≠ 0...
, the largest overring of the domain.
If the ring is not a domain, typically being integrally closed means that every local ring
Local ring
In abstract algebra, more particularly in ring theory, local rings are certain rings that are comparatively simple, and serve to describe what is called "local behaviour", in the sense of functions defined on varieties or manifolds, or of algebraic number fields examined at a particular place, or...
is an integrally closed domain.
Sometimes a domain that is integrally closed is called "normal" if it is integrally closed and being thought of as a variety.
In this respect, the normalization of a variety
Algebraic variety
In mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
(or scheme
Scheme (mathematics)
In mathematics, a scheme is an important concept connecting the fields of algebraic geometry, commutative algebra and number theory. Schemes were introduced by Alexander Grothendieck so as to broaden the notion of algebraic variety; some consider schemes to be the basic object of study of modern...
) is simply the
 of the integral closure of all of the rings.
of the integral closure of all of the rings.Ordered groups
An ordered groupOrdered group
In abstract algebra, a partially-ordered group is a group equipped with a partial order "≤" that is translation-invariant; in other words, "≤" has the property that, for all a, b, and g in G, if a ≤ b then a+g ≤ b+g and g+a ≤ g+b.An element x of G is called positive element if 0 ≤ x...
G is called integrally closed if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
for all elements a and b of G, if an ≤ b for all natural n then a ≤ 1.
This property is somewhat stronger than the fact that an ordered group is Archimedean
Archimedean property
In abstract algebra and analysis, the Archimedean property, named after the ancient Greek mathematician Archimedes of Syracuse, is a property held by some ordered or normed groups, fields, and other algebraic structures. Roughly speaking, it is the property of having no infinitely large or...
. Though for a lattice-ordered group to be integrally closed and to be Archimedean is equivalent.
We have the surprising theorem that every integrally closed directed
Directed set
In mathematics, a directed set is a nonempty set A together with a reflexive and transitive binary relation ≤ , with the additional property that every pair of elements has an upper bound: In other words, for any a and b in A there must exist a c in A with a ≤ c and b ≤...
group is already abelian
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
. This has to do with the fact that a directed group is embeddable into a complete lattice-ordered group if and only if it is integrally closed. Furthermore, every archimedean lattice-ordered group is abelian.

