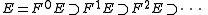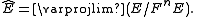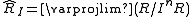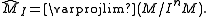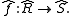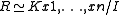Completion (ring theory)
Encyclopedia
In abstract algebra
, a completion is any of several related functor
s on ring
s and modules
that result in complete topological ring
s and modules. Completion is similar to localization
, and together they are among the most basic tools in analysing commutative ring
s. Complete commutative rings have simpler structure than the general ones and Hensel's lemma
applies to them. Geometrically, a completion of a commutative ring R concentrates on a formal neighborhood of a point or a Zariski closed
subvariety
of its spectrum
Spec R.
with a descending filtration
of subgroups, one defines the completion (with respect to the filtration) as the inverse limit
:
This is again an abelian group. Usually E is an additive abelian group. If E has additional algebraic structure compatible with the filtration, for instance E is a filtered ring
, a filtered module
, or a filtered vector space
, then its completion is again an object with the same structure that is complete in the topology determined by the filtration. This construction may be applied both to commutative
and noncommutative ring
s. As may be expected, this produces a complete topological ring
.
, the filtration on a commutative ring
R by the powers of a proper ideal
I determines the Krull topology (after Wolfgang Krull
) or I-adic topology on R. The case of a maximal ideal
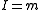 is especially important. The basis of open neighbourhoods of 0 in R is given by the powers In, which are nested and form a descending filtration on R:
is especially important. The basis of open neighbourhoods of 0 in R is given by the powers In, which are nested and form a descending filtration on R:
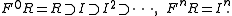
The completion is the inverse limit
of the factor rings,
. The kernel of the canonical map π from the ring to its completion is the intersection of the powers of I. Thus π is injective if and only if this intersection reduces to the zero element of the ring; by the Krull intersection theorem, this is the case for any commutative Noetherian ring
which is either an integral domain or a local ring
.
There is a related topology on R-modules, also called Krull or I-adic topology. A basis of open neighborhoods of a module
M is given by the sets of the form
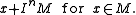
The completion of an R-module M the inverse limit of the quotients
This procedure converts any module over R into a complete topological module
over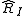 .
.
2. Let R = K[x1,…,xn] be the polynomial ring
in n variables over a field K and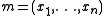 be the maximal ideal generated by the variables. Then the completion
be the maximal ideal generated by the variables. Then the completion 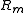 is the ring Kx1,…,xn of formal power series
is the ring Kx1,…,xn of formal power series
in n variables over K.
3. Let R be the ring of holomorphic functions on a complex manifold
and let I be the maximal ideal of functions vanishing at some point p. Then the completion of R at the ideal I is the ring of power series over C that are convergent in a neighborhood of p.
Moreover, if M and N are two modules over the same topological ring R and f: M → N is a continuous module map then f uniquely extends to the map of the completions:
2. The completion of a Noetherian ring
R is a flat module
over R.
3. The completion of a finitely generated module M over a Noetherian ring R can be obtained by extension of scalars: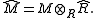
Together with the previous property, this implies that the functor of completion on finitely generated R-modules is exact
: it preserves short exact sequences.
4. Cohen
structure theorem (equicharacteristic case). Let R be a complete local
Noetherian commutative ring with maximal ideal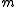 and residue field
and residue field
K. If R contains a field, then
for some n and some ideal I (Eisenbud, Theorem 7.7).
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, a completion is any of several related functor
Functor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
s on ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
s and modules
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
that result in complete topological ring
Topological ring
In mathematics, a topological ring is a ring R which is also a topological space such that both the addition and the multiplication are continuous as mapswhere R × R carries the product topology.- General comments :...
s and modules. Completion is similar to localization
Localization of a ring
In abstract algebra, localization is a systematic method of adding multiplicative inverses to a ring. Given a ring R and a subset S, one wants to construct some ring R* and ring homomorphism from R to R*, such that the image of S consists of units in R*...
, and together they are among the most basic tools in analysing commutative ring
Commutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
s. Complete commutative rings have simpler structure than the general ones and Hensel's lemma
Hensel's lemma
In mathematics, Hensel's lemma, also known as Hensel's lifting lemma, named after Kurt Hensel, is a result in modular arithmetic, stating that if a polynomial equation has a simple root modulo a prime number , then this root corresponds to a unique root of the same equation modulo any higher power...
applies to them. Geometrically, a completion of a commutative ring R concentrates on a formal neighborhood of a point or a Zariski closed
Zariski topology
In algebraic geometry, the Zariski topology is a particular topology chosen for algebraic varieties that reflects the algebraic nature of their definition. It is due to Oscar Zariski and took a place of particular importance in the field around 1950...
subvariety
Algebraic variety
In mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
of its spectrum
Spectrum of a ring
In abstract algebra and algebraic geometry, the spectrum of a commutative ring R, denoted by Spec, is the set of all proper prime ideals of R...
Spec R.
General construction
Suppose that E is an abelian groupAbelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
with a descending filtration
of subgroups, one defines the completion (with respect to the filtration) as the inverse limit
Inverse limit
In mathematics, the inverse limit is a construction which allows one to "glue together" several related objects, the precise manner of the gluing process being specified by morphisms between the objects...
:
This is again an abelian group. Usually E is an additive abelian group. If E has additional algebraic structure compatible with the filtration, for instance E is a filtered ring
Filtered algebra
In mathematics, a filtered algebra is a generalization of the notion of a graded algebra. Examples appear in many branches of mathematics, especially in homological algebra and representation theory....
, a filtered module
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
, or a filtered vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
, then its completion is again an object with the same structure that is complete in the topology determined by the filtration. This construction may be applied both to commutative
Commutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
and noncommutative ring
Noncommutative ring
In mathematics, more specifically modern algebra and ring theory, a noncommutative ring is a ring whose multiplication is not commutative; that is, if R is a noncommutative ring, there exists a and b in R with a·b ≠ b·a, and conversely.Noncommutative rings are ubiquitous in mathematics, and occur...
s. As may be expected, this produces a complete topological ring
Topological ring
In mathematics, a topological ring is a ring R which is also a topological space such that both the addition and the multiplication are continuous as mapswhere R × R carries the product topology.- General comments :...
.
Krull topology
In commutative algebraCommutative algebra
Commutative algebra is the branch of abstract algebra that studies commutative rings, their ideals, and modules over such rings. Both algebraic geometry and algebraic number theory build on commutative algebra...
, the filtration on a commutative ring
Commutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
R by the powers of a proper ideal
Ideal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
I determines the Krull topology (after Wolfgang Krull
Wolfgang Krull
Wolfgang Krull was a German mathematician working in the field of commutative algebra.He was born in Baden-Baden, Imperial Germany and died in Bonn, West Germany.- See also :* Krull dimension* Krull topology...
) or I-adic topology on R. The case of a maximal ideal
Maximal ideal
In mathematics, more specifically in ring theory, a maximal ideal is an ideal which is maximal amongst all proper ideals. In other words, I is a maximal ideal of a ring R if I is an ideal of R, I ≠ R, and whenever J is another ideal containing I as a subset, then either J = I or J = R...
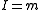 is especially important. The basis of open neighbourhoods of 0 in R is given by the powers In, which are nested and form a descending filtration on R:
is especially important. The basis of open neighbourhoods of 0 in R is given by the powers In, which are nested and form a descending filtration on R: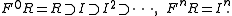
The completion is the inverse limit
Inverse limit
In mathematics, the inverse limit is a construction which allows one to "glue together" several related objects, the precise manner of the gluing process being specified by morphisms between the objects...
of the factor rings,
. The kernel of the canonical map π from the ring to its completion is the intersection of the powers of I. Thus π is injective if and only if this intersection reduces to the zero element of the ring; by the Krull intersection theorem, this is the case for any commutative Noetherian ring
Noetherian ring
In mathematics, more specifically in the area of modern algebra known as ring theory, a Noetherian ring, named after Emmy Noether, is a ring in which every non-empty set of ideals has a maximal element...
which is either an integral domain or a local ring
Local ring
In abstract algebra, more particularly in ring theory, local rings are certain rings that are comparatively simple, and serve to describe what is called "local behaviour", in the sense of functions defined on varieties or manifolds, or of algebraic number fields examined at a particular place, or...
.
There is a related topology on R-modules, also called Krull or I-adic topology. A basis of open neighborhoods of a module
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
M is given by the sets of the form
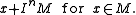
The completion of an R-module M the inverse limit of the quotients
This procedure converts any module over R into a complete topological module
Topological module
In mathematics, a topological module is a module over a topological ring such that scalar multiplication and addition are continuous.- Examples :A topological vector space is a topological module over a topological field....
over
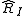 .
.Examples
1. The ring of p-adic integers Zp is obtained by completing the ring Z of integers at the ideal (p).2. Let R = K[x1,…,xn] be the polynomial ring
Polynomial ring
In mathematics, especially in the field of abstract algebra, a polynomial ring is a ring formed from the set of polynomials in one or more variables with coefficients in another ring. Polynomial rings have influenced much of mathematics, from the Hilbert basis theorem, to the construction of...
in n variables over a field K and
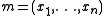 be the maximal ideal generated by the variables. Then the completion
be the maximal ideal generated by the variables. Then the completion 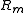 is the ring Kx1,…,xn of formal power series
is the ring Kx1,…,xn of formal power seriesFormal power series
In mathematics, formal power series are a generalization of polynomials as formal objects, where the number of terms is allowed to be infinite; this implies giving up the possibility to substitute arbitrary values for indeterminates...
in n variables over K.
3. Let R be the ring of holomorphic functions on a complex manifold
Complex manifold
In differential geometry, a complex manifold is a manifold with an atlas of charts to the open unit disk in Cn, such that the transition maps are holomorphic....
and let I be the maximal ideal of functions vanishing at some point p. Then the completion of R at the ideal I is the ring of power series over C that are convergent in a neighborhood of p.
Properties
1. The completion is a functorial operation: a continuous map f: R → S of topological rings gives rise to a map of their completions,Moreover, if M and N are two modules over the same topological ring R and f: M → N is a continuous module map then f uniquely extends to the map of the completions:
-
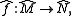 where
where 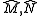 are modules over
are modules over 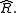
2. The completion of a Noetherian ring
Noetherian ring
In mathematics, more specifically in the area of modern algebra known as ring theory, a Noetherian ring, named after Emmy Noether, is a ring in which every non-empty set of ideals has a maximal element...
R is a flat module
Flat module
In Homological algebra, and algebraic geometry, a flat module over a ring R is an R-module M such that taking the tensor product over R with M preserves exact sequences. A module is faithfully flat if taking the tensor product with a sequence produces an exact sequence if and only if the original...
over R.
3. The completion of a finitely generated module M over a Noetherian ring R can be obtained by extension of scalars:
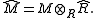
Together with the previous property, this implies that the functor of completion on finitely generated R-modules is exact
Exact functor
In homological algebra, an exact functor is a functor, from some category to another, which preserves exact sequences. Exact functors are very convenient in algebraic calculations, roughly speaking because they can be applied to presentations of objects easily...
: it preserves short exact sequences.
4. Cohen
Paul Cohen (mathematician)
Paul Joseph Cohen was an American mathematician best known for his proof of the independence of the continuum hypothesis and the axiom of choice from Zermelo–Fraenkel set theory, the most widely accepted axiomatization of set theory.-Early years:Cohen was born in Long Branch, New Jersey, into a...
structure theorem (equicharacteristic case). Let R be a complete local
Local ring
In abstract algebra, more particularly in ring theory, local rings are certain rings that are comparatively simple, and serve to describe what is called "local behaviour", in the sense of functions defined on varieties or manifolds, or of algebraic number fields examined at a particular place, or...
Noetherian commutative ring with maximal ideal
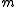 and residue field
and residue fieldResidue field
In mathematics, the residue field is a basic construction in commutative algebra. If R is a commutative ring and m is a maximal ideal, then the residue field is the quotient ring k = R/m, which is a field...
K. If R contains a field, then
for some n and some ideal I (Eisenbud, Theorem 7.7).