
Dimensionless quantity
Encyclopedia
In dimensional analysis
, a dimensionless quantity or quantity of dimension one is a quantity
without an associated physical dimension
. It is thus a "pure" number, and as such always has a dimension of 1. Dimensionless quantities are widely used in mathematics
, physics
, engineering
, economics
, and in everyday life (such as in counting). Numerous well-known quantities, such as π
, e, and φ
, are dimensionless.
Dimensionless quantities are often defined as product
s or ratio
s of quantities
that are not dimensionless, but whose dimensions cancel out when their powers
are multiplied. This is the case, for instance, with the engineering strain, a measure of deformation. It is defined as change in length over initial length but, since these quantities both have dimensions L (length), the result is a dimensionless quantity.
is that the functional
dependence between a certain number (say, n) of variables
can be reduced by the number (say, k) of independent
dimension
s occurring in those variables to give a set of p = n − k independent, dimensionless quantities
. For the purposes of the experimenter, different systems which share the same description by dimensionless quantity
are equivalent.
consumption of a stirrer with a given shape is a function of the density
and the viscosity
of the fluid to be stirred, the size of the stirrer given by its diameter
, and the speed
of the stirrer. Therefore, we have n = 5 variables representing our example.
Those n = 5 variables are built up from k = 3 dimensions which are:
According to the π-theorem, the n = 5 variables can be reduced by the k = 3 dimensions to form p = n − k = 5 − 3 = 2 independent dimensionless numbers which are, in case of the stirrer:
contemplated defining the unit of 1 as the 'uno', but the idea was dropped.
. Certain dimensionless quantities of some importance are given below:
in a vacuum, the universal gravitational constant, and the constants of Planck and Boltzmann, are normalized to 1 if the units for time
, length
, mass
, charge
, and temperature
are chosen appropriately. The resulting system of units is known as natural
. However, not all physical constant
s can be eliminated in any system of units; the values of the remaining ones must be determined experimentally. Resulting constants include:
Dimensional analysis
In physics and all science, dimensional analysis is a tool to find or check relations among physical quantities by using their dimensions. The dimension of a physical quantity is the combination of the basic physical dimensions which describe it; for example, speed has the dimension length per...
, a dimensionless quantity or quantity of dimension one is a quantity
Quantity
Quantity is a property that can exist as a magnitude or multitude. Quantities can be compared in terms of "more" or "less" or "equal", or by assigning a numerical value in terms of a unit of measurement. Quantity is among the basic classes of things along with quality, substance, change, and relation...
without an associated physical dimension
Dimensional analysis
In physics and all science, dimensional analysis is a tool to find or check relations among physical quantities by using their dimensions. The dimension of a physical quantity is the combination of the basic physical dimensions which describe it; for example, speed has the dimension length per...
. It is thus a "pure" number, and as such always has a dimension of 1. Dimensionless quantities are widely used in mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, engineering
Engineering
Engineering is the discipline, art, skill and profession of acquiring and applying scientific, mathematical, economic, social, and practical knowledge, in order to design and build structures, machines, devices, systems, materials and processes that safely realize improvements to the lives of...
, economics
Economics
Economics is the social science that analyzes the production, distribution, and consumption of goods and services. The term economics comes from the Ancient Greek from + , hence "rules of the house"...
, and in everyday life (such as in counting). Numerous well-known quantities, such as π
Pi
' is a mathematical constant that is the ratio of any circle's circumference to its diameter. is approximately equal to 3.14. Many formulae in mathematics, science, and engineering involve , which makes it one of the most important mathematical constants...
, e, and φ
Golden ratio
In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989...
, are dimensionless.
Dimensionless quantities are often defined as product
Product (mathematics)
In mathematics, a product is the result of multiplying, or an expression that identifies factors to be multiplied. The order in which real or complex numbers are multiplied has no bearing on the product; this is known as the commutative law of multiplication...
s or ratio
Ratio
In mathematics, a ratio is a relationship between two numbers of the same kind , usually expressed as "a to b" or a:b, sometimes expressed arithmetically as a dimensionless quotient of the two which explicitly indicates how many times the first number contains the second In mathematics, a ratio is...
s of quantities
Quantity
Quantity is a property that can exist as a magnitude or multitude. Quantities can be compared in terms of "more" or "less" or "equal", or by assigning a numerical value in terms of a unit of measurement. Quantity is among the basic classes of things along with quality, substance, change, and relation...
that are not dimensionless, but whose dimensions cancel out when their powers
Exponentiation
Exponentiation is a mathematical operation, written as an, involving two numbers, the base a and the exponent n...
are multiplied. This is the case, for instance, with the engineering strain, a measure of deformation. It is defined as change in length over initial length but, since these quantities both have dimensions L (length), the result is a dimensionless quantity.
Properties
- Even though a dimensionless quantity has no physical dimension associated with it, it can still have dimensionless unitsUnits of measurementA unit of measurement is a definite magnitude of a physical quantity, defined and adopted by convention and/or by law, that is used as a standard for measurement of the same physical quantity. Any other value of the physical quantity can be expressed as a simple multiple of the unit of...
(i.e. not unitless). To show the quantity being measured (for example mass fraction or mole fraction), it is sometimes helpful to use the same units in both the numerator and denominator (kg/kg or mol/mol). The quantity may also be given as a ratio of two different units that have the same dimension (for instance, light years over meters). This may be the case when calculating slopeSlopeIn mathematics, the slope or gradient of a line describes its steepness, incline, or grade. A higher slope value indicates a steeper incline....
s in graphs, or when making unit conversions. Such notation does not indicate the presence of physical dimensions, and is purely a notational convention. Other common dimensionless units are % (= 0.01), ‰ (= 0.001), ppm (= 10−6), ppb (= 10−9), pptParts-per notationIn science and engineering, the parts-per notation is a set of pseudo units to describe small values of miscellaneous dimensionless quantities, e.g. mole fraction or mass fraction. Since these fractions are quantity-per-quantity measures, they are pure numbers with no associated units of measurement...
(= 10−12) and angle units (degrees, radians, grad). Units of amount such as the dozenDozenA dozen is a grouping of approximately twelve. The dozen may be one of the earliest primitive groupings, perhaps because there are approximately a dozen cycles of the moon or months in a cycle of the sun or year...
and the grossGross (unit)A gross is equal to a dozen dozen, i.e. 12 × 12 = 144.It can be used in duodecimal counting. The use of gross likely originated from the fact that 144 can be counted on the fingers using the fingertips and first two joints of each finger when marked by the thumb of one hand. The other hand...
are also dimensionless. - The ratio of two quantities with the same dimensions is dimensionless, and has the same value regardless of the units used to calculate them. For instance, if body A exerts a force of magnitude F on body B, and B exerts a force of magnitude f on A, then the ratio F/f will always be equal to 1, regardless of the actual units used to measure F and f. This is a fundamental property of dimensionless proportions and follows from the assumption that the laws of physics are independent of the system of units used in their expression. In this case, if the ratio F/f was not always equal to 1, but changed if we switched from SISiSi, si, or SI may refer to :- Measurement, mathematics and science :* International System of Units , the modern international standard version of the metric system...
to CGS, for instance, that would mean that Newton's Third Law's truth or falsity would depend on the system of units used, which would contradict this fundamental hypothesis. The assumption that the laws of physics are not contingent upon a specific unit system is also closely related to the Buckingham π theorem. A formulation of this theorem is that any physical law can be expressed as an identityIdentity (mathematics)In mathematics, the term identity has several different important meanings:*An identity is a relation which is tautologically true. This means that whatever the number or value may be, the answer stays the same. For example, algebraically, this occurs if an equation is satisfied for all values of...
(always true equationEquationAn equation is a mathematical statement that asserts the equality of two expressions. In modern notation, this is written by placing the expressions on either side of an equals sign , for examplex + 3 = 5\,asserts that x+3 is equal to 5...
) involving only dimensionless combinations (ratios or products) of the variables linked by the law (e. g., pressure and volume are linked by Boyle's LawBoyle's lawBoyle's law is one of many gas laws and a special case of the ideal gas law. Boyle's law describes the inversely proportional relationship between the absolute pressure and volume of a gas, if the temperature is kept constant within a closed system...
– they are inversely proportional). If the dimensionless combinations' values changed with the systems of units, then the equation would not be an identity, and Buckingham's theorem would not hold.
Buckingham π theorem
Another consequence of the Buckingham π theorem of dimensional analysisDimensional analysis
In physics and all science, dimensional analysis is a tool to find or check relations among physical quantities by using their dimensions. The dimension of a physical quantity is the combination of the basic physical dimensions which describe it; for example, speed has the dimension length per...
is that the functional
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
dependence between a certain number (say, n) of variables
Variable (mathematics)
In mathematics, a variable is a value that may change within the scope of a given problem or set of operations. In contrast, a constant is a value that remains unchanged, though often unknown or undetermined. The concepts of constants and variables are fundamental to many areas of mathematics and...
can be reduced by the number (say, k) of independent
Independent variable
The terms "dependent variable" and "independent variable" are used in similar but subtly different ways in mathematics and statistics as part of the standard terminology in those subjects...
dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
s occurring in those variables to give a set of p = n − k independent, dimensionless quantities
Quantity
Quantity is a property that can exist as a magnitude or multitude. Quantities can be compared in terms of "more" or "less" or "equal", or by assigning a numerical value in terms of a unit of measurement. Quantity is among the basic classes of things along with quality, substance, change, and relation...
. For the purposes of the experimenter, different systems which share the same description by dimensionless quantity
Quantity
Quantity is a property that can exist as a magnitude or multitude. Quantities can be compared in terms of "more" or "less" or "equal", or by assigning a numerical value in terms of a unit of measurement. Quantity is among the basic classes of things along with quality, substance, change, and relation...
are equivalent.
Example
The powerElectric power
Electric power is the rate at which electric energy is transferred by an electric circuit. The SI unit of power is the watt.-Circuits:Electric power, like mechanical power, is represented by the letter P in electrical equations...
consumption of a stirrer with a given shape is a function of the density
Density
The mass density or density of a material is defined as its mass per unit volume. The symbol most often used for density is ρ . In some cases , density is also defined as its weight per unit volume; although, this quantity is more properly called specific weight...
and the viscosity
Viscosity
Viscosity is a measure of the resistance of a fluid which is being deformed by either shear or tensile stress. In everyday terms , viscosity is "thickness" or "internal friction". Thus, water is "thin", having a lower viscosity, while honey is "thick", having a higher viscosity...
of the fluid to be stirred, the size of the stirrer given by its diameter
Diameter
In geometry, a diameter of a circle is any straight line segment that passes through the center of the circle and whose endpoints are on the circle. The diameters are the longest chords of the circle...
, and the speed
Speed
In kinematics, the speed of an object is the magnitude of its velocity ; it is thus a scalar quantity. The average speed of an object in an interval of time is the distance traveled by the object divided by the duration of the interval; the instantaneous speed is the limit of the average speed as...
of the stirrer. Therefore, we have n = 5 variables representing our example.
Those n = 5 variables are built up from k = 3 dimensions which are:
- Length: L (m)
- Time: T (s)
- Mass: M (kg).
According to the π-theorem, the n = 5 variables can be reduced by the k = 3 dimensions to form p = n − k = 5 − 3 = 2 independent dimensionless numbers which are, in case of the stirrer:
- Reynolds number (a dimensionless number describing the fluid flow regime)
- Power numberPower numberThe power number Np is a commonly-used dimensionless number relating the resistance force to the inertia force.The power-number has different specifications according to the field of application...
(describing the stirrer and also involves the density of the fluid)
Standards efforts
The International Committee for Weights and MeasuresInternational Committee for Weights and Measures
The Interglobal Committee for Weights and Measures is the English name of the Comité international des poids et mesures . It consists of eighteen persons from Member States of the Metre Convention...
contemplated defining the unit of 1 as the 'uno', but the idea was dropped.
Examples
- Consider this example: Sarah says, "Out of every 10 apples I gather, 1 is rotten.". The rotten-to-gathered ratio is (1 apple) / (10 apples) = 0.1 = 10%, which is a dimensionless quantity.
- Another more typical example in physics and engineering is the measure of plane angles. An angle is measured as the ratio of the length of a circle's arc subtended by an angle whose vertex is the centre of the circle to some other length. The ratio, length divided by length, is dimensionless. When using radians as the unit, the length that is compared is the length of the radius of the circle. When using degreeDegree (angle)A degree , usually denoted by ° , is a measurement of plane angle, representing 1⁄360 of a full rotation; one degree is equivalent to π/180 radians...
as the units, the arc's length is compared to 1/360 of the circumference of the circle. - In the case of the dimensionless quantity π, being the ratio of a circle's circumference to its diameter, the number would be constant regardless of what unit is used to measure a circle's circumference and diameter (eg. centimetres, miles, light-years, etc), as long as the same unit is used for both.
List of dimensionless quantities
All numbers are dimensionless quantitiesQuantity
Quantity is a property that can exist as a magnitude or multitude. Quantities can be compared in terms of "more" or "less" or "equal", or by assigning a numerical value in terms of a unit of measurement. Quantity is among the basic classes of things along with quality, substance, change, and relation...
. Certain dimensionless quantities of some importance are given below:
| Name | Standard symbol | Definition | Field of application |
|---|---|---|---|
| Abbe number Abbe number In physics and optics, the Abbe number, also known as the V-number or constringence of a transparent material, is a measure of the material's dispersion in relation to the refractive index... |
V | optics Optics Optics is the branch of physics which involves the behavior and properties of light, including its interactions with matter and the construction of instruments that use or detect it. Optics usually describes the behavior of visible, ultraviolet, and infrared light... (dispersion Dispersion (optics) In optics, dispersion is the phenomenon in which the phase velocity of a wave depends on its frequency, or alternatively when the group velocity depends on the frequency.Media having such a property are termed dispersive media... in optical materials) |
|
| Activity coefficient Activity coefficient An activity coefficient is a factor used in thermodynamics to account for deviations from ideal behaviour in a mixture of chemical substances. In an ideal mixture, the interactions between each pair of chemical species are the same and, as a result, properties of the mixtures can be expressed... |
γ | chemistry Chemistry Chemistry is the science of matter, especially its chemical reactions, but also its composition, structure and properties. Chemistry is concerned with atoms and their interactions with other atoms, and particularly with the properties of chemical bonds.... (Proportion of "active" molecules or atoms) |
|
| Albedo Albedo Albedo , or reflection coefficient, is the diffuse reflectivity or reflecting power of a surface. It is defined as the ratio of reflected radiation from the surface to incident radiation upon it... |
 |
climatology Climatology Climatology is the study of climate, scientifically defined as weather conditions averaged over a period of time, and is a branch of the atmospheric sciences... , astronomy Astronomy Astronomy is a natural science that deals with the study of celestial objects and phenomena that originate outside the atmosphere of Earth... (reflectivity Reflectivity In optics and photometry, reflectivity is the fraction of incident radiation reflected by a surface. In general it must be treated as a directional property that is a function of the reflected direction, the incident direction, and the incident wavelength... of surfaces or bodies) |
|
| Archimedes number | Ar | motion of fluid Fluid In physics, a fluid is a substance that continually deforms under an applied shear stress. Fluids are a subset of the phases of matter and include liquids, gases, plasmas and, to some extent, plastic solids.... s due to density Density The mass density or density of a material is defined as its mass per unit volume. The symbol most often used for density is ρ . In some cases , density is also defined as its weight per unit volume; although, this quantity is more properly called specific weight... differences |
|
| Arrhenius number |  |
Ratio of activation energy Activation energy In chemistry, activation energy is a term introduced in 1889 by the Swedish scientist Svante Arrhenius that is defined as the energy that must be overcome in order for a chemical reaction to occur. Activation energy may also be defined as the minimum energy required to start a chemical reaction... to thermal energy Thermal energy Thermal energy is the part of the total internal energy of a thermodynamic system or sample of matter that results in the system's temperature.... |
|
| Atomic weight Atomic weight Atomic weight is a dimensionless physical quantity, the ratio of the average mass of atoms of an element to 1/12 of the mass of an atom of carbon-12... |
M | chemistry Chemistry Chemistry is the science of matter, especially its chemical reactions, but also its composition, structure and properties. Chemistry is concerned with atoms and their interactions with other atoms, and particularly with the properties of chemical bonds.... |
|
| Bagnold number Bagnold Number The Bagnold number is the ratio of grain collision stresses to viscous fluid stresses in a granular flow with interstitial Newtonian fluid, first identified by Ralph Alger Bagnold.The Bagnold number is defined by... |
Ba | flow of bulk solids such as grain GRAIN GRAIN is a small international non-profit organisation that works to support small farmers and social movements in their struggles for community-controlled and biodiversity-based food systems. Our support takes the form of independent research and analysis, networking at local, regional and... and sand Sand Sand is a naturally occurring granular material composed of finely divided rock and mineral particles.The composition of sand is highly variable, depending on the local rock sources and conditions, but the most common constituent of sand in inland continental settings and non-tropical coastal... . |
|
| Blowdown circulation number | BC | deviation from isothermal flow in blowdown (rapid depressurization) of a pressure vessel | |
| Bejan number Bejan number There are two Bejan numbers in use, named after Duke University professor Adrian Bejan in two scientific domains: thermodynamics and fluid mechanics.-Thermodynamics:... (thermodynamics) |
Be | the ratio of heat transfer irreversibility to total irreversibility due to heat transfer and fluid friction | |
| Bejan number Bejan number There are two Bejan numbers in use, named after Duke University professor Adrian Bejan in two scientific domains: thermodynamics and fluid mechanics.-Thermodynamics:... (fluid mechanics) |
Be | dimensionless pressure drop along a channel | |
| Bingham number | Bm | 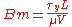 |
Ratio of yield stress to viscous stress |
| Bingham capillary number | Bm.Ca |  |
Ratio of yield stress to capillary pressure |
| Biot number Biot number The Biot number is a dimensionless number used in non-steady-state heat transfer calculations. It is named after the French physicist Jean-Baptiste Biot , and gives a simple index of the ratio of the heat transfer resistances inside of and at the surface of a body... |
Bi | surface vs. volume conductivity of solids | |
| Blake number Blake number The Blake number in fluid mechanics is a nondimensional number showing the ratio of inertial force to viscous force.It is used in momentum transfer in general and in particular for flow of a fluid through beds of solids... |
Bl or B | relative importance of inertia compared to viscous forces in fluid flow through porous media | |
| Bodenstein number | Bo |  |
residence-time Residence time Residence time is the average amount of time that a particle spends in a particular system. This measurement varies directly with the amount of substance that is present in the system.... distribution |
| Bond number | Bo | capillary action Capillary action Capillary action, or capilarity, is the ability of a liquid to flow against gravity where liquid spontanously rise in a narrow space such as between the hair of a paint-brush, in a thin tube, or in porous material such as paper or in some non-porous material such as liquified carbon fiber, or in a... driven by buoyancy Buoyancy In physics, buoyancy is a force exerted by a fluid that opposes an object's weight. In a column of fluid, pressure increases with depth as a result of the weight of the overlying fluid. Thus a column of fluid, or an object submerged in the fluid, experiences greater pressure at the bottom of the... |
|
| Brinkman number Brinkman number The Brinkman number is a dimensionless number related to heat conduction from a wall to a flowing viscous fluid, commonly used in polymer processing... |
Br | heat transfer by conduction from the wall to a viscous fluid | |
| Brownell–Katz number | combination of capillary number Capillary number In fluid dynamics, the capillary number represents the relative effect of viscous forces versus surface tension acting across an interface between a liquid and a gas, or between two immiscible liquids... and Bond number |
||
| Capillary number Capillary number In fluid dynamics, the capillary number represents the relative effect of viscous forces versus surface tension acting across an interface between a liquid and a gas, or between two immiscible liquids... |
Ca | fluid flow influenced by surface tension Surface tension Surface tension is a property of the surface of a liquid that allows it to resist an external force. It is revealed, for example, in floating of some objects on the surface of water, even though they are denser than water, and in the ability of some insects to run on the water surface... |
|
| Coefficient of static friction |
 |
friction of solid bodies at rest | |
| Coefficient of kinetic friction |
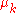 |
friction of solid bodies in translational motion | |
| Colburn j factor Chilton and Colburn J-factor analogy Chilton–Colburn J-factor analogy is a successful and widely used analogy from heat, momentum, and mass transfer analogies. The basic mechanisms and mathematics of heat, mass, and momentum transport are essentially the same... |
dimensionless heat transfer coefficient | ||
| Courant–Friedrich–Levy number |
 |
numerical solutions of hyperbolic PDEs | |
| Damkohler number | Da |  |
reaction time scales vs. resonance time |
| Damping ratio Damping ratio [[Image:Damped spring.gif|right|frame|Underdamped [[spring–mass system]] with ζ 1 , and is referred to as overdamped.*Underdamped:If s is a complex number, then the solution is a decaying exponential combined with an oscillatory portion that looks like \exp... |
 |
 |
the level of damping Damping In physics, damping is any effect that tends to reduce the amplitude of oscillations in an oscillatory system, particularly the harmonic oscillator.In mechanics, friction is one such damping effect... in a system |
| Darcy friction factor | 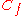 or or  |
fluid flow | |
| Dean number Dean number The Dean number is a dimensionless group in fluid mechanics, which occurs in the study of flow in curved pipes and channels. It is named after the British scientist W. R. Dean, who studied such flows in the 1920s .- Definition :... |
D | vortices in curved ducts | |
| Deborah number Deborah number The Deborah number is a dimensionless number, often used in rheology to characterize the fluidity of materials under specific flow conditions. It was originally proposed by Markus Reiner, a professor at Technion in Israel, inspired by a verse in the Bible, stating "The mountains flowed before the... |
De | rheology Rheology Rheology is the study of the flow of matter, primarily in the liquid state, but also as 'soft solids' or solids under conditions in which they respond with plastic flow rather than deforming elastically in response to an applied force.... of viscoelastic fluids |
|
| Decibel Decibel The decibel is a logarithmic unit that indicates the ratio of a physical quantity relative to a specified or implied reference level. A ratio in decibels is ten times the logarithm to base 10 of the ratio of two power quantities... |
dB | ratio of two intensities, often sound | |
| Drag coefficient Drag coefficient In fluid dynamics, the drag coefficient is a dimensionless quantity that is used to quantify the drag or resistance of an object in a fluid environment such as air or water. It is used in the drag equation, where a lower drag coefficient indicates the object will have less aerodynamic or... |
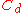 |
flow resistance | |
| Dukhin number Dukhin number Dukhin number is a dimensionless quantity that characterizes the contribution of the surface conductivity to various electrokinetic and electroacoustic effects, as well as to electrical conductivity and permittivity of fluid heterogeneous systems.... |
Du | ratio of electric surface conductivity Surface conductivity Surface conductivity is an additional conductivity of an electrolyte in the vicinity of charged surfaces. Close to charged surfaces a layer of counter ions of opposite polarity exists which is attracted by the surface charges. This layer of higher ionic concentration is a part of the interfacial ... to the electric bulk conductivity in heterogeneous systems |
|
| Euler's number | e | mathematics Mathematics Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity... |
|
| Eckert number Eckert number The Eckert number is a dimentionless number used in fluid dynamics. It expresses the relationship between a flow's kinetic energy and enthalpy, and is used to characterize dissipation. It is named after Ernst R. G... |
Ec | convective heat transfer | |
| Ekman number Ekman number The Ekman number is a dimensionless number used in describing geophysical phenomena in the oceans and atmosphere. It characterises the ratio of viscous forces in a fluid to the fictitious forces arising from planetary rotation... |
Ek | geophysics Geophysics Geophysics is the physics of the Earth and its environment in space; also the study of the Earth using quantitative physical methods. The term geophysics sometimes refers only to the geological applications: Earth's shape; its gravitational and magnetic fields; its internal structure and... (frictional (viscous Viscosity Viscosity is a measure of the resistance of a fluid which is being deformed by either shear or tensile stress. In everyday terms , viscosity is "thickness" or "internal friction". Thus, water is "thin", having a lower viscosity, while honey is "thick", having a higher viscosity... ) forces) |
|
| Elasticity (economics) Elasticity (economics) In economics, elasticity is the measurement of how changing one economic variable affects others. For example:* "If I lower the price of my product, how much more will I sell?"* "If I raise the price, how much less will I sell?"... |
E | widely used to measure how demand or supply responds to price changes | |
| Eötvös number Eötvös number In fluid dynamics the Eötvös number is a dimensionless number named after Hungarian physicist Loránd Eötvös . It is also known as the Bond number... |
Eo | determination of bubble/drop shape | |
| Ericksen number | Er | liquid crystal flow behavior | |
| Euler number Euler number (physics) The Euler number is a dimensionless number used in fluid flow calculations. It expresses the relationship between a local pressure drop e.g. over a restriction and the kinetic energy per volume, and is used to characterize losses in the flow, where a perfect frictionless flow corresponds to an... |
Eu | hydrodynamics (pressure forces vs. inertia forces) | |
| Fanning friction factor | f | fluid flow in pipes | |
| Feigenbaum constants Feigenbaum constants The Feigenbaum constants are two mathematical constants named after the mathematician Mitchell Feigenbaum. Both express ratios in a bifurcation diagram.The first Feigenbaum constant ,... |
 |
chaos theory Chaos theory Chaos theory is a field of study in mathematics, with applications in several disciplines including physics, economics, biology, and philosophy. Chaos theory studies the behavior of dynamical systems that are highly sensitive to initial conditions, an effect which is popularly referred to as the... (period doubling) |
|
| Fine structure constant |  |
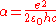 |
quantum electrodynamics Quantum electrodynamics Quantum electrodynamics is the relativistic quantum field theory of electrodynamics. In essence, it describes how light and matter interact and is the first theory where full agreement between quantum mechanics and special relativity is achieved... (QED) |
| f-number F-number In optics, the f-number of an optical system expresses the diameter of the entrance pupil in terms of the focal length of the lens; in simpler terms, the f-number is the focal length divided by the "effective" aperture diameter... |
 |
optics Optics Optics is the branch of physics which involves the behavior and properties of light, including its interactions with matter and the construction of instruments that use or detect it. Optics usually describes the behavior of visible, ultraviolet, and infrared light... , photography Photography Photography is the art, science and practice of creating durable images by recording light or other electromagnetic radiation, either electronically by means of an image sensor or chemically by means of a light-sensitive material such as photographic film... |
|
| Foppl–von Karman number | thin-shell buckling | ||
| Fourier number Fourier number In physics and engineering, the Fourier number or Fourier modulus, named after Joseph Fourier, is a dimensionless number that characterizes heat conduction. Conceptually, it is the ratio of the heat conduction rate to the rate of thermal energy storage. Together with the Biot number, it... |
Fo | heat Heat In physics and thermodynamics, heat is energy transferred from one body, region, or thermodynamic system to another due to thermal contact or thermal radiation when the systems are at different temperatures. It is often described as one of the fundamental processes of energy transfer between... transfer |
|
| Fresnel number Fresnel number The Fresnel number F, named after the physicist Augustin-Jean Fresnel, is a dimensionless number occurring in optics, in particular in diffraction theory.... |
F | slit diffraction Diffraction Diffraction refers to various phenomena which occur when a wave encounters an obstacle. Italian scientist Francesco Maria Grimaldi coined the word "diffraction" and was the first to record accurate observations of the phenomenon in 1665... |
|
| Froude number Froude number The Froude number is a dimensionless number defined as the ratio of a characteristic velocity to a gravitational wave velocity. It may equivalently be defined as the ratio of a body's inertia to gravitational forces. In fluid mechanics, the Froude number is used to determine the resistance of an... |
Fr | 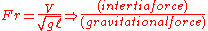 |
wave Wave In physics, a wave is a disturbance that travels through space and time, accompanied by the transfer of energy.Waves travel and the wave motion transfers energy from one point to another, often with no permanent displacement of the particles of the medium—that is, with little or no associated mass... and surface behaviour |
| Gain Gain In electronics, gain is a measure of the ability of a circuit to increase the power or amplitude of a signal from the input to the output. It is usually defined as the mean ratio of the signal output of a system to the signal input of the same system. It may also be defined on a logarithmic scale,... |
electronics Electronics Electronics is the branch of science, engineering and technology that deals with electrical circuits involving active electrical components such as vacuum tubes, transistors, diodes and integrated circuits, and associated passive interconnection technologies... (signal output to signal input) |
||
| Gain Ratio | system of representing bicycle Bicycle A bicycle, also known as a bike, pushbike or cycle, is a human-powered, pedal-driven, single-track vehicle, having two wheels attached to a frame, one behind the other. A person who rides a bicycle is called a cyclist, or bicyclist.... gearing |
||
| Galilei number Galilei number In fluid dynamics, the Galilei number , sometimes also referred to as Galileo number , is a dimensionless number named after Italian scientist Galileo Galilei .... |
Ga | gravity-driven viscous flow | |
| Golden ratio Golden ratio In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989... |
 |
mathematics Mathematics Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity... and aesthetics Aesthetics Aesthetics is a branch of philosophy dealing with the nature of beauty, art, and taste, and with the creation and appreciation of beauty. It is more scientifically defined as the study of sensory or sensori-emotional values, sometimes called judgments of sentiment and taste... |
|
| Graetz number | Gz | heat Heat In physics and thermodynamics, heat is energy transferred from one body, region, or thermodynamic system to another due to thermal contact or thermal radiation when the systems are at different temperatures. It is often described as one of the fundamental processes of energy transfer between... flow |
|
| Grashof number | Gr | free convection Convection Convection is the movement of molecules within fluids and rheids. It cannot take place in solids, since neither bulk current flows nor significant diffusion can take place in solids.... |
|
| Gravitational coupling constant Gravitational coupling constant In physics, the gravitational coupling constant, αG, is the coupling constant characterizing the gravitational attraction between two charged elementary particles having nonzero mass... |
 |
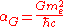 |
Gravitation Gravitation Gravitation, or gravity, is a natural phenomenon by which physical bodies attract with a force proportional to their mass. Gravitation is most familiar as the agent that gives weight to objects with mass and causes them to fall to the ground when dropped... |
| Hatta number | Ha | adsorption enhancement due to chemical reaction | |
| Hagen number Hagen number The Hagen number is a dimensionless number used in forced flow calculations. It is the forced flow equivalent of the Grashof number and was named after the German hydraulic engineer G. H. L... |
Hg | forced convection | |
| Hydraulic gradient | i | groundwater Groundwater Groundwater is water located beneath the ground surface in soil pore spaces and in the fractures of rock formations. A unit of rock or an unconsolidated deposit is called an aquifer when it can yield a usable quantity of water. The depth at which soil pore spaces or fractures and voids in rock... flow |
|
| Jakob Number | Ja | 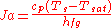 |
Ratio of sensible to latent energy absorbed during liquid-vapor phase change |
| Karlovitz number | turbulent combustion turbulent combustion | ||
| Keulegan–Carpenter number Keulegan–Carpenter number In fluid dynamics, the Keulegan–Carpenter number, also called the period number, is a dimensionless quantity describing the relative importance of the drag forces over inertia forces for bluff objects in an oscillatory fluid flow. Or similarly, for objects that oscillate in a fluid at rest... |
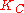 |
ratio of drag force to inertia Inertia Inertia is the resistance of any physical object to a change in its state of motion or rest, or the tendency of an object to resist any change in its motion. It is proportional to an object's mass. The principle of inertia is one of the fundamental principles of classical physics which are used to... for a bluff object in oscillatory Oscillation Oscillation is the repetitive variation, typically in time, of some measure about a central value or between two or more different states. Familiar examples include a swinging pendulum and AC power. The term vibration is sometimes used more narrowly to mean a mechanical oscillation but sometimes... fluid flow |
|
| Knudsen number Knudsen number The Knudsen number is a dimensionless number defined as the ratio of the molecular mean free path length to a representative physical length scale. This length scale could be, for example, the radius of a body in a fluid... |
Kn | ratio of the molecular mean free path Mean free path In physics, the mean free path is the average distance covered by a moving particle between successive impacts which modify its direction or energy or other particle properties.-Derivation:... length to a representative physical length scale |
|
| Kt/V Kt/V In medicine, Kt/V is a number used to quantify hemodialysis and peritoneal dialysis treatment adequacy.*K - dialyzer clearance of urea*t - dialysis time*V - volume of distribution of urea, approximately equal to patient's total body water... |
medicine Medicine Medicine is the science and art of healing. It encompasses a variety of health care practices evolved to maintain and restore health by the prevention and treatment of illness.... |
||
| Kutateladze number | K | counter-current two-phase flow | |
| Laplace number Laplace number The Laplace number , also known as the Suratman number , is a dimensionless number used in the characterization of free surface fluid dynamics... |
La | free convection within immiscible Miscibility Miscibility is the property of liquids to mix in all proportions, forming a homogeneous solution. In principle, the term applies also to other phases , but the main focus is usually on the solubility of one liquid in another... fluids |
|
| Lewis number | Le | ratio of mass diffusivity and thermal diffusivity | |
| Lift coefficient Lift coefficient The lift coefficient is a dimensionless coefficient that relates the lift generated by a lifting body, the dynamic pressure of the fluid flow around the body, and a reference area associated with the body... |
 |
lift Lift (force) A fluid flowing past the surface of a body exerts a surface force on it. Lift is the component of this force that is perpendicular to the oncoming flow direction. It contrasts with the drag force, which is the component of the surface force parallel to the flow direction... available from an airfoil Airfoil An airfoil or aerofoil is the shape of a wing or blade or sail as seen in cross-section.... at a given angle of attack Angle of attack Angle of attack is a term used in fluid dynamics to describe the angle between a reference line on a lifting body and the vector representing the relative motion between the lifting body and the fluid through which it is moving... |
|
| Lockhart–Martinelli parameter |
 |
flow of wet gas Wet gas A wet gas is any gas with a small amount of liquid present. The term "wet gas" has been used to describe a range of conditions ranging from a humid gas which is gas saturated with liquid vapour to a multiphase flow with a 90% volume of gas... es |
|
| Love number Love number The Love numbers h, k, and l are dimensionless parameters that measure the rigidity of a planetary body and the susceptibility of its shape to change in response to a tidal potential.... |
measuring the solidity of the earth | ||
| Lundquist number Lundquist number In plasma physics, the Lundquist number is the dimensionless ratio of an Alfvén wave crossing timescale to a resistive diffusion timescale... |
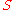 |
ratio of a resistive time to an Alfvén wave Alfvén wave An Alfvén wave, named after Hannes Alfvén, is a type of magnetohydrodynamic wave.-Definition:An Alfvén wave in a plasma is a low-frequency travelling oscillation of the ions and the magnetic field... crossing time in a plasma |
|
| Mach number Mach number Mach number is the speed of an object moving through air, or any other fluid substance, divided by the speed of sound as it is in that substance for its particular physical conditions, including those of temperature and pressure... |
M | Ratio of current speed to the speed of sound, i.e. Mach 1 is the speed of sound, Mach 0.5 is half the speed of sound, Mach 2 is twice the speed of sound. | gas dynamics Gas dynamics Gas dynamics is a branch of fluid dynamics concerned with studying the motion of gases and its consequent effects. Gas dynamics combines the principles of fluid mechanics and thermodynamics... |
| Magnetic Reynolds number Magnetic Reynolds number The Magnetic Reynolds number is a dimensionless group thatoccurs in magnetohydrodynamics. It gives an estimate of the effects of magnetic advection to magnetic diffusion, and is typically defined by:where* U is a typical velocity scale of the flow... |
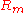 |
magnetohydrodynamics Magnetohydrodynamics Magnetohydrodynamics is an academic discipline which studies the dynamics of electrically conducting fluids. Examples of such fluids include plasmas, liquid metals, and salt water or electrolytes... |
|
| Manning roughness coefficient Manning formula The Manning formula, known also as the Gauckler–Manning formula, or Gauckler–Manning–Strickler formula in Europe, is an empirical formula for open channel flow, or free-surface flow driven by gravity... |
n | open channel flow Manning formula The Manning formula, known also as the Gauckler–Manning formula, or Gauckler–Manning–Strickler formula in Europe, is an empirical formula for open channel flow, or free-surface flow driven by gravity... (flow driven by gravity) |
|
| Marangoni number Marangoni number The Marangoni number is a dimensionless number named after Italian scientist Carlo Marangoni.The Marangoni number may be regarded as proportional to surface tension forces divided by viscous forces... |
Mg | Marangoni flow due to thermal surface tension deviations | |
| Morton number Morton number In fluid dynamics, the Morton number is a dimensionless number used together with the Eötvös number to characterize the shape of bubbles or drops moving in a surrounding fluid or continuous phase, c.The Morton number is defined as... |
Mo | determination of bubble/drop shape | |
| Mpemba number | 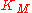 |
thermal conduction and diffusion in freezing of a solution | |
| Nusselt number Nusselt number In heat transfer at a boundary within a fluid, the Nusselt number is the ratio of convective to conductive heat transfer across the boundary. Named after Wilhelm Nusselt, it is a dimensionless number... |
Nu | 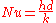 |
heat transfer Heat transfer Heat transfer is a discipline of thermal engineering that concerns the exchange of thermal energy from one physical system to another. Heat transfer is classified into various mechanisms, such as heat conduction, convection, thermal radiation, and phase-change transfer... with forced convection Convection Convection is the movement of molecules within fluids and rheids. It cannot take place in solids, since neither bulk current flows nor significant diffusion can take place in solids.... |
| Ohnesorge number | Oh | atomization of liquids, Marangoni flow | |
| Péclet number Péclet number The Péclet number is a dimensionless number relevant in the study of transport phenomena in fluid flows. It is named after the French physicist Jean Claude Eugène Péclet. It is defined to be the ratio of the rate of advection of a physical quantity by the flow to the rate of diffusion of the same... |
Pe | 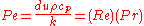 |
advection Advection Advection, in chemistry, engineering and earth sciences, is a transport mechanism of a substance, or a conserved property, by a fluid, due to the fluid's bulk motion in a particular direction. An example of advection is the transport of pollutants or silt in a river. The motion of the water carries... –diffusion Diffusion Molecular diffusion, often called simply diffusion, is the thermal motion of all particles at temperatures above absolute zero. The rate of this movement is a function of temperature, viscosity of the fluid and the size of the particles... problems; relates total momentun transfer to molecular heat transfer. |
| Peel number | adhesion of microstructures with substrate | ||
| Perveance Perveance Perveance is a notion used in the description of charged particle beams. The value of perveance indicates how significant the space charge effect is on the beam’s motion... |
K | measure of the strength of space charge in a charged particle beam | |
| Pi Pi ' is a mathematical constant that is the ratio of any circle's circumference to its diameter. is approximately equal to 3.14. Many formulae in mathematics, science, and engineering involve , which makes it one of the most important mathematical constants... |
 |
mathematics Mathematics Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity... (ratio of a circle's circumference to its diameter) |
|
| Poisson's ratio Poisson's ratio Poisson's ratio , named after Siméon Poisson, is the ratio, when a sample object is stretched, of the contraction or transverse strain , to the extension or axial strain .... |
 |
elasticity Elasticity (physics) In physics, elasticity is the physical property of a material that returns to its original shape after the stress that made it deform or distort is removed. The relative amount of deformation is called the strain.... (load in transverse and longitudinal direction) |
|
| Porosity Porosity Porosity or void fraction is a measure of the void spaces in a material, and is a fraction of the volume of voids over the total volume, between 0–1, or as a percentage between 0–100%... |
 |
geology Geology Geology is the science comprising the study of solid Earth, the rocks of which it is composed, and the processes by which it evolves. Geology gives insight into the history of the Earth, as it provides the primary evidence for plate tectonics, the evolutionary history of life, and past climates... |
|
| Power factor Power factor The power factor of an AC electric power system is defined as the ratio of the real power flowing to the load over the apparent power in the circuit, and is a dimensionless number between 0 and 1 . Real power is the capacity of the circuit for performing work in a particular time... |
electronics Electronics Electronics is the branch of science, engineering and technology that deals with electrical circuits involving active electrical components such as vacuum tubes, transistors, diodes and integrated circuits, and associated passive interconnection technologies... (real power to apparent power) |
||
| Power number Power number The power number Np is a commonly-used dimensionless number relating the resistance force to the inertia force.The power-number has different specifications according to the field of application... |
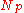 |
power consumption by agitators | |
| Prandtl number | Pr | 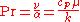 |
convection Convection Convection is the movement of molecules within fluids and rheids. It cannot take place in solids, since neither bulk current flows nor significant diffusion can take place in solids.... heat transfer Heat transfer Heat transfer is a discipline of thermal engineering that concerns the exchange of thermal energy from one physical system to another. Heat transfer is classified into various mechanisms, such as heat conduction, convection, thermal radiation, and phase-change transfer... (thickness of thermal and momentum boundary layers) |
| also known as thermicity factor | ratio of heat evolution to heat conduction within a catalyst pellet | ||
| Pressure coefficient Pressure coefficient The pressure coefficient is a dimensionless number which describes the relative pressures throughout a flow field in fluid dynamics. The pressure coefficient is used in aerodynamics and hydrodynamics... |
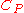 |
pressure experienced at a point on an airfoil | |
| Q factor Q factor In physics and engineering the quality factor or Q factor is a dimensionless parameter that describes how under-damped an oscillator or resonator is, or equivalently, characterizes a resonator's bandwidth relative to its center frequency.... |
 |
describes how under-damped Damping In physics, damping is any effect that tends to reduce the amplitude of oscillations in an oscillatory system, particularly the harmonic oscillator.In mechanics, friction is one such damping effect... an oscillator Oscillation Oscillation is the repetitive variation, typically in time, of some measure about a central value or between two or more different states. Familiar examples include a swinging pendulum and AC power. The term vibration is sometimes used more narrowly to mean a mechanical oscillation but sometimes... or resonator Resonator A resonator is a device or system that exhibits resonance or resonant behavior, that is, it naturally oscillates at some frequencies, called its resonant frequencies, with greater amplitude than at others. The oscillations in a resonator can be either electromagnetic or mechanical... is |
|
| Radian Radian Radian is the ratio between the length of an arc and its radius. The radian is the standard unit of angular measure, used in many areas of mathematics. The unit was formerly a SI supplementary unit, but this category was abolished in 1995 and the radian is now considered a SI derived unit... |
rad | measurement of angles | |
| Rayleigh number Rayleigh number In fluid mechanics, the Rayleigh number for a fluid is a dimensionless number associated with buoyancy driven flow... |
Ra | buoyancy and viscous forces in free convection | |
| Refractive index Refractive index In optics the refractive index or index of refraction of a substance or medium is a measure of the speed of light in that medium. It is expressed as a ratio of the speed of light in vacuum relative to that in the considered medium.... |
n | electromagnetism, optics | |
| Reynolds number | Re |  |
Ratio of fluid inertial and viscous forces |
| Relative density Relative density Relative density, or specific gravity, is the ratio of the density of a substance to the density of a given reference material. Specific gravity usually means relative density with respect to water... |
RD | hydrometer Hydrometer A hydrometer is an instrument used to measure the specific gravity of liquids; that is, the ratio of the density of the liquid to the density of water.... s, material comparisons |
|
| Richardson number | Ri | effect of buoyancy on flow stability | |
| Rockwell scale Rockwell scale The Rockwell scale is a hardness scale based on the indentation hardness of a material. The Rockwell test determines the hardness by measuring the depth of penetration of an indenter under a large load compared to the penetration made by a preload. There are different scales, denoted by a single... |
mechanical hardness | ||
| Rolling resistance coefficient | Crr | 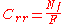 |
vehicle dynamics Vehicle dynamics Vehicle dynamics refers to the dynamics of vehicles, here assumed to be ground vehicles. Vehicle dynamics is a part of engineering primarily based on classical mechanics but it may also involve chemistry, solid state physics, electrical engineering, communications, psychology, control theory,... |
| Rossby number Rossby number The Rossby number, named for Carl-Gustav Arvid Rossby, is a dimensionless number used in describing fluid flow. The Rossby number is the ratio of inertial to Coriolis force, terms v\cdot\nabla v\sim U^2 / L and \Omega\times v\sim U\Omega in the Navier–Stokes equations, respectively... |
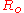 |
inertial forces in geophysics Geophysics Geophysics is the physics of the Earth and its environment in space; also the study of the Earth using quantitative physical methods. The term geophysics sometimes refers only to the geological applications: Earth's shape; its gravitational and magnetic fields; its internal structure and... |
|
| Rouse number Rouse number The Rouse number is a non-dimensional number in fluid dynamics which is used to define a concentration profile of suspended sediment and which also determines how sediment will be transported in a flowing fluid... |
Z or P | sediment transport Sediment transport Sediment transport is the movement of solid particles , typically due to a combination of the force of gravity acting on the sediment, and/or the movement of the fluid in which the sediment is entrained... |
|
| Schmidt number Schmidt number Schmidt number is a dimensionless number defined as the ratio of momentum diffusivity and mass diffusivity, and is used to characterize fluid flows in which there are simultaneous momentum and mass diffusion convection processes... |
Sc | fluid dynamics (mass transfer and diffusion Diffusion Molecular diffusion, often called simply diffusion, is the thermal motion of all particles at temperatures above absolute zero. The rate of this movement is a function of temperature, viscosity of the fluid and the size of the particles... ) |
|
| Shape factor | H | ratio of displacement thickness to momentum thickness in boundary layer flow | |
| Sherwood number | Sh | mass transfer with forced convection | |
| Shields parameter Shields parameter The Shields parameter, also called the Shields criterion or Shields number, is a nondimensional number used to calculate the initiation of motion of sediment in a fluid flow. It is a nondimensionalization of a shear stress, and is typically denoted \tau_\ast or \theta... |
τ∗ or θ | threshold of sediment movement Sediment transport Sediment transport is the movement of solid particles , typically due to a combination of the force of gravity acting on the sediment, and/or the movement of the fluid in which the sediment is entrained... due to fluid motion |
|
| Sommerfeld number Sommerfeld number In the design of fluid bearings, the Sommerfeld number, or bearing characteristic number, is a dimensionless quantity used extensively in hydrodynamic lubrication analysis... |
boundary lubrication Lubrication Lubrication is the process, or technique employed to reduce wear of one or both surfaces in close proximity, and moving relative to each another, by interposing a substance called lubricant between the surfaces to carry or to help carry the load between the opposing surfaces. The interposed... |
||
| Stanton number Stanton number The Stanton number, St or CH, is a dimensionless number that measures the ratio of heat transferred into a fluid to the thermal capacity of fluid... |
St | heat transfer in forced convection Convection Convection is the movement of molecules within fluids and rheids. It cannot take place in solids, since neither bulk current flows nor significant diffusion can take place in solids.... |
|
| Stefan number | Ste | heat transfer during phase change | |
| Stokes number Stokes number The Stokes number, named after Irish mathematician George Gabriel Stokes, is a dimensionless number corresponding to the behavior of particles suspended in a fluid flow... |
Stk or  |
particle dynamics in a fluid stream | |
| Strain Strain (materials science) In continuum mechanics, the infinitesimal strain theory, sometimes called small deformation theory, small displacement theory, or small displacement-gradient theory, deals with infinitesimal deformations of a continuum body... |
 |
materials science Materials science Materials science is an interdisciplinary field applying the properties of matter to various areas of science and engineering. This scientific field investigates the relationship between the structure of materials at atomic or molecular scales and their macroscopic properties. It incorporates... , elasticity Elasticity (physics) In physics, elasticity is the physical property of a material that returns to its original shape after the stress that made it deform or distort is removed. The relative amount of deformation is called the strain.... |
|
| Strouhal number Strouhal number In dimensional analysis, the Strouhal number is a dimensionless number describing oscillating flow mechanisms. The parameter is named after Vincenc Strouhal, a Czech physicist who experimented in 1878 with wires experiencing vortex shedding and singing in the wind... |
St or Sr | nondimensional frequency, continuous and pulsating flow | |
| Taylor number Taylor number In fluid dynamics, the Taylor number is a dimensionless quantity that characterizes the importance of centrifugal "forces" or so-called inertial forces due to rotation of a fluid about an axis, relative to viscous forces. The typical context of the Taylor number is in characterization of the... |
Ta | rotating fluid flows | |
| Ursell number Ursell number In fluid dynamics, the Ursell number indicates the nonlinearity of long surface gravity waves on a fluid layer. This dimensionless parameter is named after Fritz Ursell, who discussed its significance in 1953.... |
U | nonlinearity of surface gravity waves Ocean surface wave In fluid dynamics, wind waves or, more precisely, wind-generated waves are surface waves that occur on the free surface of oceans, seas, lakes, rivers, and canals or even on small puddles and ponds. They usually result from the wind blowing over a vast enough stretch of fluid surface. Waves in the... on a shallow fluid layer |
|
| Vadasz number | Va | 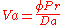 |
governs the effects of porosity  , the Prandtl number and the Darcy number on flow in a porous medium , the Prandtl number and the Darcy number on flow in a porous medium |
| van 't Hoff factor Van 't Hoff factor The van 't Hoff factor i is a measure of the effect of a solute upon colligative properties, such as vapor pressure, osmotic pressure and freezing point depression. The van 't Hoff factor is the ratio between the actual concentration of particles produced when the substance is dissolved, and the... |
i | quantitative analysis Quantitative analysis (chemistry) In chemistry, quantitative analysis is the determination of the absolute or relative abundance of one, several or all particular substance present in a sample.... (Kf Freezing-point depression Freezing-point depression describes the phenomenon in which the freezing point of a liquid is depressed when another compound is added, meaning that a solution has a lower freezing point than a pure solvent. This happens whenever a non-volatile solute is added to a pure solvent, such as water... and Kb) |
|
| Wallis parameter | J* | nondimensional superficial velocity Superficial velocity Superficial velocity , in engineering of multiphase flows and flows in porous media, is an hypothetical fluid velocity calculated as if the given phase or fluid were the only one flowing or present in a given cross sectional area. Other phases, particles, the skeleton of the porous medium, etc... in multiphase flows |
|
| Weaver flame speed number | laminar burning velocity relative to hydrogen Hydrogen Hydrogen is the chemical element with atomic number 1. It is represented by the symbol H. With an average atomic weight of , hydrogen is the lightest and most abundant chemical element, constituting roughly 75% of the Universe's chemical elemental mass. Stars in the main sequence are mainly... gas |
||
| Weber number Weber number The Weber number is a dimensionless number in fluid mechanics that is often useful in analysing fluid flows where there is an interface between two different fluids, especially for multiphase flows with strongly curved surfaces. It can be thought of as a measure of the relative importance of the... |
We | multiphase flow with strongly curved surfaces | |
| Weissenberg number Weissenberg number The Weissenberg number is a dimensionless number used in the study of viscoelastic flows. It is named after Karl Weissenberg. The dimensionless number is the ratio of the relaxation time of the fluid and a specific process time... |
Wi | viscoelastic flows | |
| Womersley number Womersley number The Womersley number is a dimensionless number in biofluid mechanics. It is a dimensionless expression of the pulsatile flow frequency in relation to viscous effects. It is named after John R. Womersley . The Womersley number is important in keeping dynamic similarity when scaling an experiment. An... |
 |
continuous and pulsating flows |
Dimensionless physical constants
Certain fundamental physical constants, such as the speed of lightSpeed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
in a vacuum, the universal gravitational constant, and the constants of Planck and Boltzmann, are normalized to 1 if the units for time
Time
Time is a part of the measuring system used to sequence events, to compare the durations of events and the intervals between them, and to quantify rates of change such as the motions of objects....
, length
Length
In geometric measurements, length most commonly refers to the longest dimension of an object.In certain contexts, the term "length" is reserved for a certain dimension of an object along which the length is measured. For example it is possible to cut a length of a wire which is shorter than wire...
, mass
Mass
Mass can be defined as a quantitive measure of the resistance an object has to change in its velocity.In physics, mass commonly refers to any of the following three properties of matter, which have been shown experimentally to be equivalent:...
, charge
Electric charge
Electric charge is a physical property of matter that causes it to experience a force when near other electrically charged matter. Electric charge comes in two types, called positive and negative. Two positively charged substances, or objects, experience a mutual repulsive force, as do two...
, and temperature
Temperature
Temperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot...
are chosen appropriately. The resulting system of units is known as natural
Natural units
In physics, natural units are physical units of measurement based only on universal physical constants. For example the elementary charge e is a natural unit of electric charge, or the speed of light c is a natural unit of speed...
. However, not all physical constant
Physical constant
A physical constant is a physical quantity that is generally believed to be both universal in nature and constant in time. It can be contrasted with a mathematical constant, which is a fixed numerical value but does not directly involve any physical measurement.There are many physical constants in...
s can be eliminated in any system of units; the values of the remaining ones must be determined experimentally. Resulting constants include:
- α, the fine structure constant, the coupling constantCoupling constantIn physics, a coupling constant, usually denoted g, is a number that determines the strength of an interaction. Usually the Lagrangian or the Hamiltonian of a system can be separated into a kinetic part and an interaction part...
for the electromagnetic interaction; - μ or β, the proton-to-electron mass ratioProton-to-electron mass ratioIn physics, the proton-to-electron mass ratio, μ or β, is simply the rest mass of the proton divided by that of the electron...
, the rest mass of the protonProtonThe proton is a subatomic particle with the symbol or and a positive electric charge of 1 elementary charge. One or more protons are present in the nucleus of each atom, along with neutrons. The number of protons in each atom is its atomic number....
divided by that of the electronElectronThe electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
. More generally, the rest masses of all elementary particles relative to that of the electron; - αs, the coupling constantCoupling constantIn physics, a coupling constant, usually denoted g, is a number that determines the strength of an interaction. Usually the Lagrangian or the Hamiltonian of a system can be separated into a kinetic part and an interaction part...
for the strong force; - αG, the gravitational coupling constantGravitational coupling constantIn physics, the gravitational coupling constant, αG, is the coupling constant characterizing the gravitational attraction between two charged elementary particles having nonzero mass...
.
See also
- Similitude (model)Similitude (model)Similitude is a concept applicable to the testing of engineering models. A model is said to have similitude with the real application if the two share geometric similarity, kinematic similarity and dynamic similarity...
- Orders of magnitude (numbers)Orders of magnitude (numbers)This list contains selected positive numbers in increasing order, including counts of things, dimensionless quantity and probabilities. Each number is given a name in the short scale, which is used in English speaking countries, as well as a name in the long scale, which is used in some of the...
- Dimensional analysisDimensional analysisIn physics and all science, dimensional analysis is a tool to find or check relations among physical quantities by using their dimensions. The dimension of a physical quantity is the combination of the basic physical dimensions which describe it; for example, speed has the dimension length per...
- Normalization (statistics)Normalization (statistics)In one usage in statistics, normalization is the process of isolating statistical error in repeated measured data. A normalization is sometimes based on a property...
and standardized moment, the analogous concepts in statisticsStatisticsStatistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments.... - Buckingham π theorem
External links
- John Baez, " How Many Fundamental Constants Are There?"
- Huba, J. D., 2007, NRL Plasma Formulary: Dimensionless Numbers of Fluid Mechanics. Naval Research LaboratoryUnited States Naval Research LaboratoryThe United States Naval Research Laboratory is the corporate research laboratory for the United States Navy and the United States Marine Corps and conducts a program of scientific research and development. NRL opened in 1923 at the instigation of Thomas Edison...
. p. 23, 24, 25 - Sheppard, Mike, 2007, "Systematic Search for Expressions of Dimensionless Constants using the NIST database of Physical Constants."

