
Dean number
Encyclopedia
The Dean number is a dimensionless group
in fluid mechanics
, which occurs in the study of flow in curved pipes and channels. It is named after the British scientist W. R. Dean
, who studied such flows in the 1920s (Dean, 1927, 1928).
where
The Dean number is therefore the product of the Reynolds number (based on axial flow through a pipe of diameter
through a pipe of diameter  ) and the square root of the curvature ratio.
) and the square root of the curvature ratio.
for the steady axially uniform flow of a Newtonian fluid
in a toroidal
pipe, obtained by retaining just the leading order curvature effects (i.e. the leading-order equations for ).
).
We use an orthogonal coordinates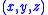 with corresponding unit vectors
with corresponding unit vectors  aligned with the centre-line of the pipe at each point. The axial direction is
aligned with the centre-line of the pipe at each point. The axial direction is  , with
, with  being the normal in the plane of the centre-line, and
being the normal in the plane of the centre-line, and  the binormal. For an axial flow driven by a pressure gradient
the binormal. For an axial flow driven by a pressure gradient  , the axial velocity
, the axial velocity  is scaled with
is scaled with  . The cross-stream velocities
. The cross-stream velocities  are scaled with
are scaled with 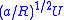 , and cross-stream pressures with
, and cross-stream pressures with 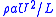 . Lengths are scaled with the tube radius
. Lengths are scaled with the tube radius  .
.
In terms of these non-dimensional variables and coordinates, the Dean equations are then


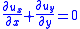
where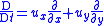
is the convective derivative
.
The Dean number D is the only parameter left in the system, and encapsulates the leading order curvature effects. Higher-order approximations will involve additional parameters.
For weak curvature effects (small D), the Dean equations can be solved as a series expansion in D. The first correction to the leading-order axial Poiseuille flow is a pair of vortices in the cross-section carrying flow form the inside to the outrside of the bend across the centre and back around the edges. This solution is stable up to a critical Dean number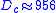 (Dennis & Ng 1982). For larger D, there are multiple solutions, many of which are unstable.
(Dennis & Ng 1982). For larger D, there are multiple solutions, many of which are unstable.
Dimensionless quantity
In dimensional analysis, a dimensionless quantity or quantity of dimension one is a quantity without an associated physical dimension. It is thus a "pure" number, and as such always has a dimension of 1. Dimensionless quantities are widely used in mathematics, physics, engineering, economics, and...
in fluid mechanics
Fluid mechanics
Fluid mechanics is the study of fluids and the forces on them. Fluid mechanics can be divided into fluid statics, the study of fluids at rest; fluid kinematics, the study of fluids in motion; and fluid dynamics, the study of the effect of forces on fluid motion...
, which occurs in the study of flow in curved pipes and channels. It is named after the British scientist W. R. Dean
W. R. Dean
W. R. Dean was a British applied mathematician and fluid dynamicist. His research interests included Stokes flow, solid mechanics, and flow in curved channels. The Dean number bears his name....
, who studied such flows in the 1920s (Dean, 1927, 1928).
Definition
The Dean number is typically denoted by the symbol De. For flow in a pipe or tube it is defined as:where
-
 is the density of the fluid
is the density of the fluid -
 is the dynamic viscosity
is the dynamic viscosity -
 is the axial velocity scale
is the axial velocity scale -
 is the diameter (other shapes are represented by an equivalent diameter, see Reynolds number)
is the diameter (other shapes are represented by an equivalent diameter, see Reynolds number) -
 is the radius of curvature of the path of the channel.
is the radius of curvature of the path of the channel.
The Dean number is therefore the product of the Reynolds number (based on axial flow
 through a pipe of diameter
through a pipe of diameter  ) and the square root of the curvature ratio.
) and the square root of the curvature ratio.The Dean Equations
The Dean number appears in the so-called Dean Equations. These are an approximation to the full Navier–Stokes equationsNavier-Stokes equations
In physics, the Navier–Stokes equations, named after Claude-Louis Navier and George Gabriel Stokes, describe the motion of fluid substances. These equations arise from applying Newton's second law to fluid motion, together with the assumption that the fluid stress is the sum of a diffusing viscous...
for the steady axially uniform flow of a Newtonian fluid
Newtonian fluid
A Newtonian fluid is a fluid whose stress versus strain rate curve is linear and passes through the origin. The constant of proportionality is known as the viscosity.-Definition:...
in a toroidal
Torus
In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
pipe, obtained by retaining just the leading order curvature effects (i.e. the leading-order equations for
 ).
).We use an orthogonal coordinates
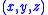 with corresponding unit vectors
with corresponding unit vectors  aligned with the centre-line of the pipe at each point. The axial direction is
aligned with the centre-line of the pipe at each point. The axial direction is  , with
, with  being the normal in the plane of the centre-line, and
being the normal in the plane of the centre-line, and  the binormal. For an axial flow driven by a pressure gradient
the binormal. For an axial flow driven by a pressure gradient  , the axial velocity
, the axial velocity  is scaled with
is scaled with  . The cross-stream velocities
. The cross-stream velocities  are scaled with
are scaled with 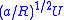 , and cross-stream pressures with
, and cross-stream pressures with 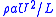 . Lengths are scaled with the tube radius
. Lengths are scaled with the tube radius  .
.In terms of these non-dimensional variables and coordinates, the Dean equations are then



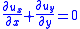
where
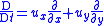
is the convective derivative
Convective derivative
The material derivative is a derivative taken along a path moving with velocity v, and is often used in fluid mechanics and classical mechanics...
.
The Dean number D is the only parameter left in the system, and encapsulates the leading order curvature effects. Higher-order approximations will involve additional parameters.
For weak curvature effects (small D), the Dean equations can be solved as a series expansion in D. The first correction to the leading-order axial Poiseuille flow is a pair of vortices in the cross-section carrying flow form the inside to the outrside of the bend across the centre and back around the edges. This solution is stable up to a critical Dean number
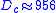 (Dennis & Ng 1982). For larger D, there are multiple solutions, many of which are unstable.
(Dennis & Ng 1982). For larger D, there are multiple solutions, many of which are unstable.


