Buoyancy
Overview
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
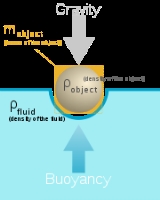
, buoyancy (icon) is a force exerted by a fluid that opposes an object's weight. In a column of fluid, pressure increases with depth as a result of the weight of the overlying fluid. Thus a column of fluid, or an object submerged in the fluid, experiences greater pressure at the bottom of the column than at the top. This difference in pressure results in a net force that tends to accelerate an object upwards.
Unanswered Questions

