Taylor number
Encyclopedia
In fluid dynamics
, the Taylor number is a dimensionless quantity
that characterizes the importance of centrifugal "forces" or so-called inertial forces due to rotation
of a fluid
about an axis, relative to viscous forces
. The typical context of the Taylor number is in characterization of the Couette flow between rotating colinear cylinders or rotating concentric spheres. In the case of a system which is not rotating uniformly, such as the case of cylindrical Couette flow
in the case where the outer cylinder is stationary and the inner cylinder is rotating, inertial forces will often tend to destabilize a system, whereas viscous forces tend to stabilize a system and damp out perturbations and turbulence.
On the other hand, in other cases the effect of rotation can be stabilizing. For example, in the case of cylindrical Couette flow with positive Rayleigh discriminant, there are no axisymmetric instabilities. Another example is a bucket of water that is rotating uniformly (i.e. undergoing solid body rotation). Here the fluid is subject to the Taylor-Proudman theorem which says that small motions will tend to produce purely two-dimensional perturbations to the overall rotational flow. However, in this case the effects of rotation and viscosity are usually characterized by the Ekman number
and the Rossby number
rather than by the Taylor number.
There are various definitions of the Taylor number which are not all equivalent, but most commonly it is given by
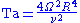
where
is a characteristic angular velocity, 
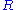is a characteristic linear dimension perpendicular to the rotation axis, and 
is the kinematic viscosity
.
In the case of inertial instability such as Taylor–Couette flow
, the Taylor number is mathematically analogous to the Grashof number which characterizes the strength of buoyant forces relative to viscous forces in convection. When the former exceeds the latter by a critical ratio, convective instability sets in. Likewise, in various systems and geometries, when the Taylor number exceeds a critical value, inertial instabilities set in, sometimes known as Taylor instabilities, which may lead to Taylor vortices or cells.
A Taylor–Couette flow describe the fluid behavior between 2 concentric cylinders in rotation. The Taylor number definition in this case (as described in the reference book "M. Frank White, Fluid Mechanics, 3rd edition, McGraw-Hill,inc., eq.4.147 at page 239" ISBN 0-07-911695-7)
R_1 = external radius of internal cylinder, R_2 = internal radius of external cylinder
Critical Ta≈1700 (G.I.Taylor,1923)
Taylor refers to the British physicist Geoffrey Ingram Taylor
(1886-1975).
Fluid dynamics
In physics, fluid dynamics is a sub-discipline of fluid mechanics that deals with fluid flow—the natural science of fluids in motion. It has several subdisciplines itself, including aerodynamics and hydrodynamics...
, the Taylor number is a dimensionless quantity
Dimensionless quantity
In dimensional analysis, a dimensionless quantity or quantity of dimension one is a quantity without an associated physical dimension. It is thus a "pure" number, and as such always has a dimension of 1. Dimensionless quantities are widely used in mathematics, physics, engineering, economics, and...
that characterizes the importance of centrifugal "forces" or so-called inertial forces due to rotation
Rotation
A rotation is a circular movement of an object around a center of rotation. A three-dimensional object rotates always around an imaginary line called a rotation axis. If the axis is within the body, and passes through its center of mass the body is said to rotate upon itself, or spin. A rotation...
of a fluid
Fluid
In physics, a fluid is a substance that continually deforms under an applied shear stress. Fluids are a subset of the phases of matter and include liquids, gases, plasmas and, to some extent, plastic solids....
about an axis, relative to viscous forces
Viscosity
Viscosity is a measure of the resistance of a fluid which is being deformed by either shear or tensile stress. In everyday terms , viscosity is "thickness" or "internal friction". Thus, water is "thin", having a lower viscosity, while honey is "thick", having a higher viscosity...
. The typical context of the Taylor number is in characterization of the Couette flow between rotating colinear cylinders or rotating concentric spheres. In the case of a system which is not rotating uniformly, such as the case of cylindrical Couette flow
Couette flow
In fluid dynamics, Couette flow refers to the laminar flow of a viscous fluid in the space between two parallel plates, one of which is moving relative to the other. The flow is driven by virtue of viscous drag force acting on the fluid and the applied pressure gradient parallel to the plates...
in the case where the outer cylinder is stationary and the inner cylinder is rotating, inertial forces will often tend to destabilize a system, whereas viscous forces tend to stabilize a system and damp out perturbations and turbulence.
On the other hand, in other cases the effect of rotation can be stabilizing. For example, in the case of cylindrical Couette flow with positive Rayleigh discriminant, there are no axisymmetric instabilities. Another example is a bucket of water that is rotating uniformly (i.e. undergoing solid body rotation). Here the fluid is subject to the Taylor-Proudman theorem which says that small motions will tend to produce purely two-dimensional perturbations to the overall rotational flow. However, in this case the effects of rotation and viscosity are usually characterized by the Ekman number
Ekman number
The Ekman number is a dimensionless number used in describing geophysical phenomena in the oceans and atmosphere. It characterises the ratio of viscous forces in a fluid to the fictitious forces arising from planetary rotation...
and the Rossby number
Rossby number
The Rossby number, named for Carl-Gustav Arvid Rossby, is a dimensionless number used in describing fluid flow. The Rossby number is the ratio of inertial to Coriolis force, terms v\cdot\nabla v\sim U^2 / L and \Omega\times v\sim U\Omega in the Navier–Stokes equations, respectively...
rather than by the Taylor number.
There are various definitions of the Taylor number which are not all equivalent, but most commonly it is given by
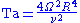
where
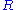is a characteristic angular velocity, is a characteristic linear dimension perpendicular to the rotation axis, and is the kinematic viscosityViscosity
Viscosity is a measure of the resistance of a fluid which is being deformed by either shear or tensile stress. In everyday terms , viscosity is "thickness" or "internal friction". Thus, water is "thin", having a lower viscosity, while honey is "thick", having a higher viscosity...
.
In the case of inertial instability such as Taylor–Couette flow
Taylor–Couette flow
In fluid dynamics, the Taylor–Couette flow consists of a viscous fluid confined in the gap between two rotating cylinders. For low angular velocities, measured by the Reynolds number Re, the flow is steady and purely azimuthal. This basic state is known as circular Couette flow, after Maurice...
, the Taylor number is mathematically analogous to the Grashof number which characterizes the strength of buoyant forces relative to viscous forces in convection. When the former exceeds the latter by a critical ratio, convective instability sets in. Likewise, in various systems and geometries, when the Taylor number exceeds a critical value, inertial instabilities set in, sometimes known as Taylor instabilities, which may lead to Taylor vortices or cells.
A Taylor–Couette flow describe the fluid behavior between 2 concentric cylinders in rotation. The Taylor number definition in this case (as described in the reference book "M. Frank White, Fluid Mechanics, 3rd edition, McGraw-Hill,inc., eq.4.147 at page 239" ISBN 0-07-911695-7)
R_1 = external radius of internal cylinder, R_2 = internal radius of external cylinder
Critical Ta≈1700 (G.I.Taylor,1923)
Taylor refers to the British physicist Geoffrey Ingram Taylor
Geoffrey Ingram Taylor
Sir Geoffrey Ingram Taylor OM was a British physicist, mathematician and expert on fluid dynamics and wave theory. His biographer and one-time student, George Batchelor, described him as "one of the most notable scientists of this century".-Biography:Taylor was born in St. John's Wood, London...
(1886-1975).