
Diffraction
Encyclopedia
Diffraction refers to various phenomena which occur when a wave encounters an obstacle. Italian scientist Francesco Maria Grimaldi
coined the word "diffraction" and was the first to record accurate observations of the phenomenon in 1665. In classical physics, the diffraction phenomenon is described as the apparent bending of waves around small obstacles and the spreading out of waves past small openings. Similar effects occur when light waves travel through a medium with a varying refractive index
or a sound wave through one with varying acoustic impedance
. Diffraction occurs with all waves, including sound
waves, water
waves, and electromagnetic waves
such as visible light
, x-ray
s and radio waves
. As physical objects have wave-like properties (at the atomic level), diffraction also occurs with matter and can be studied according to the principles of quantum mechanics
.
Richard Feynman
said that
He suggested that when there are only a few sources, say two, we call it interference, as in Young's slits, but with a large number of sources, the process is labelled diffraction.
While diffraction occurs whenever propagating waves encounter such changes, its effects are generally most pronounced for waves where the wavelength
is roughly similar to the dimensions of the diffracting objects. If the obstructing object provides multiple, closely spaced openings, a complex pattern of varying intensity can result. This is due to the superposition, or interference, of different parts of a wave that traveled to the observer by different paths (see diffraction grating
).
The formalism of diffraction can also describe the way in which waves of finite extent propagate in free space. For example, the expanding profile of a laser beam, the beam shape of a radar antenna and the field of view of an ultrasonic transducer can all be analysed using diffraction equations.
 The effects of diffraction are often seen in everyday life. The most striking examples of diffraction are those involving light; for example, the closely spaced tracks on a CD or DVD act as a diffraction grating
The effects of diffraction are often seen in everyday life. The most striking examples of diffraction are those involving light; for example, the closely spaced tracks on a CD or DVD act as a diffraction grating
to form the familiar rainbow pattern seen when looking at a disk. This principle can be extended to engineer a grating with a structure such that it will produce any diffraction pattern desired; the hologram
on a credit card is an example. Diffraction in the atmosphere
by small particles can cause a bright ring to be visible around a bright light source like the sun or the moon. A shadow of a solid object, using light from a compact source, shows small fringes near its edges. The speckle pattern
which is observed when laser light falls on an optically rough surface is also a diffraction phenomenon. All these effects are a consequence of the fact that light propagates as a wave
.
Diffraction can occur with any kind of wave. Ocean waves diffract around jetties
and other obstacles. Sound waves can diffract around objects, which is why one can still hear someone calling even when hiding behind a tree.
Diffraction can also be a concern in some technical applications; it sets a fundamental limit to the resolution of a camera, telescope, or microscope.
 The effects of diffraction of light were first carefully observed and characterized by Francesco Maria Grimaldi
The effects of diffraction of light were first carefully observed and characterized by Francesco Maria Grimaldi
, who also coined the term diffraction, from the Latin diffringere, 'to break into pieces', referring to light breaking up into different directions. The results of Grimaldi's observations were published posthumously in 1665. Isaac Newton
studied these effects and attributed them to inflexion of light rays. James Gregory
(1638–1675) observed the diffraction patterns caused by a bird feather, which was effectively the first diffraction grating to be discovered. Thomas Young
performed a celebrated experiment in 1803 demonstrating interference from two closely spaced slits. Explaining his results by interference of the waves emanating from the two different slits, he deduced that light must propagate as waves. Augustin-Jean Fresnel
did more definitive studies and calculations of diffraction, made public in 1815 and 1818, and thereby gave great support to the wave theory of light that had been advanced by Christiaan Huygens and reinvigorated by Young, against Newton's particle theory.
 Diffraction arises because of the way in which waves propagate; this is described by the Huygens–Fresnel principle and the principle of superposition of waves
Diffraction arises because of the way in which waves propagate; this is described by the Huygens–Fresnel principle and the principle of superposition of waves
. The propagation of a wave can be visualized by considering every point on a wavefront as a point source for a secondary spherical wave. The wave displacement at any subsequent point is the sum of these secondary waves. When waves are added together, their sum is determined by the relative phases as well as the amplitudes of the individual waves so that the summed amplitude of the waves can have any value between zero and the sum of the individual amplitudes. Hence, diffraction patterns usually have a series of maxima and minima.
There are various analytical models which allow the diffracted field to be calculated, including the Kirchhoff-Fresnel diffraction equation
which is derived from wave equation
, the Fraunhofer diffraction
approximation of the Kirchhoff equation which applies to the far field and the Fresnel diffraction
approximation which applies to the near field. Most configurations cannot be solved analytically, but can yield numerical solutions through finite element and boundary element methods.
It is possible to obtain a qualitative understanding of many diffraction phenomena by considering how the relative phases of the individual secondary wave sources vary, and in particular, the conditions in which the phase difference equals half a cycle in which case waves will cancel one another out.
The simplest descriptions of diffraction are those in which the situation can be reduced to a two-dimensional problem. For water waves, this is already the case; water waves propagate only on the surface of the water. For light, we can often neglect one direction if the diffracting object extends in that direction over a distance far greater than the wavelength. In the case of light shining through small circular holes we will have to take into account the full three dimensional nature of the problem.

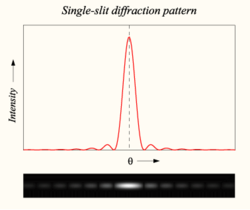 A long slit of infinitesimal width which is illuminated by light diffracts the light into a series of circular waves and the wavefront which emerges from the slit is a cylindrical wave of uniform intensity.
A long slit of infinitesimal width which is illuminated by light diffracts the light into a series of circular waves and the wavefront which emerges from the slit is a cylindrical wave of uniform intensity.
A slit which is wider than a wavelength produces interference effects in the space downstream of the slit. These can be explained by assuming that the slit behaves as though it has a large number of point sources spaced evenly across the width of the slit. The analysis of this system is simplified if we consider light of a single wavelength. If the incident light is monochromatic, these sources all have the same phase. Light incident at a given point in the space downstream of the slit is made up of contributions from each of these point sources and if the relative phases of these contributions vary by 2π or more, we may expect to find minima and maxima in the diffracted light. Such phase differences are caused by differences in the path lengths over which contributing rays reach the point from the slit.
We can find the angle at which a first minimum is obtained in the diffracted light by the following reasoning. The light from a source located at the top edge of the slit interferes destructively with a source located at the middle of the slit, when the path difference between them is equal to λ/2. Similarly, the source just below the top of the slit will interfere destructively with the source located just below the middle of the slit at the same angle. We can continue this reasoning along the entire height of the slit to conclude that the condition for destructive interference for the entire slit is the same as the condition for destructive interference between two narrow slits a distance apart that is half the width of the slit. The path difference is given by so that the minimum intensity occurs at an angle θmin given by
so that the minimum intensity occurs at an angle θmin given by

where
A similar argument can be used to show that if we imagine the slit to be divided into four, six, eight parts, etc., minima are obtained at angles θn given by
where
There is no such simple argument to enable us to find the maxima of the diffraction pattern. The intensity profile can be calculated using the Fraunhofer diffraction
equation as
where
This analysis applies only to the far field, that is, at a distance much larger than the width of the slit.


where
The light diffracted by a grating is found by summing the light diffracted from each of the elements, and is essentially a convolution
of diffraction and interference patterns.
The figure shows the light diffracted by 2-element and 5-element gratings where the grating spacings are the same; it can be seen that the maxima are in the same position, but the detailed structures of the intensities are different.


where a is the radius of the circular aperture, k is equal to 2π/λ and J1 is a Bessel function
. The smaller the aperture, the larger the spot size at a given distance, and the greater the divergence of the diffracted beams.
 at location r that is given by the solution of the frequency domain
at location r that is given by the solution of the frequency domain
wave equation
for a point source (The Helmholtz Equation
),

where is the 3-dimensional delta function. The delta function has only radial dependence, so the Laplace operator
is the 3-dimensional delta function. The delta function has only radial dependence, so the Laplace operator
(aka scalar Laplacian) in the spherical coordinate system
simplifies to (see del in cylindrical and spherical coordinates
)

By direct substitution, the solution to this equation can be readily shown to be the scalar Green's function
, which in the spherical coordinate system
(and using the physics time convention ) is:
) is:

This solution assumes that the delta function source is located at the origin. If the source is located at an arbitrary source point, denoted by the vector and the field point is located at the point
and the field point is located at the point  , then we may represent the scalar Green's function
, then we may represent the scalar Green's function
(for arbitrary source location) as:

Therefore, if an electric field, Einc(x,y) is incident on the aperture, the field produced by this aperture distribution is given by the surface integral
:

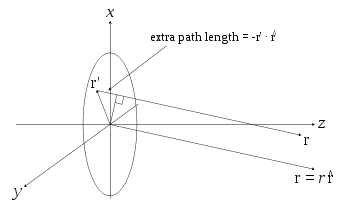 where the source point in the aperture is given by the vector
where the source point in the aperture is given by the vector

In the far field, wherein the parallel rays approximation can be employed, the Green's function,

simplifies to

as can be seen in the figure to the right (click to enlarge).
The expression for the far-zone (Fraunhofer region) field becomes

Now, since

and

the expression for the Fraunhofer region field from a planar aperture now becomes,

Letting,

and

the Fraunhofer region field of the planar aperture assumes the form of a Fourier transform

In the far-field / Fraunhofer region, this becomes the spatial Fourier transform
of the aperture distribution. Huygens' principle when applied to an aperture simply says that the far-field diffraction pattern is the spatial Fourier transform of the aperture shape, and this is a direct by-product of using the parallel-rays approximation, which is identical to doing a plane wave decomposition of the aperture plane fields (see Fourier optics
).
of a laser beam
changes as it propagates is determined by diffraction. The output mirror of the laser is an aperture, and the subsequent beam shape is determined by that aperture. Hence, the smaller the output beam, the quicker it diverges. Diode lasers have much greater divergence than He–Ne lasers for this reason.
Paradoxically, it is possible to reduce the divergence of a laser beam by first expanding it with one convex lens, and then collimating it with a second convex lens whose focal point is coincident with that of the first lens. The resulting beam has a larger aperture, and hence a lower divergence.
 The ability of an imaging system to resolve detail is ultimately limited by diffraction
The ability of an imaging system to resolve detail is ultimately limited by diffraction
. This is because a plane wave incident on a circular lens or mirror is diffracted as described above. The light is not focused to a point but forms an Airy disk having a central spot in the focal plane with radius to first null of

where λ is the wavelength of the light and N is the f-number
(focal length divided by diameter) of the imaging optics. In object space, the corresponding angular resolution
is

where D is the diameter of the entrance pupil
of the imaging lens (e.g., of a telescope's main mirror).
Two point sources will each produce an Airy pattern – see the photo of a binary star. As the point sources move closer together, the patterns will start to overlap, and ultimately they will merge to form a single pattern, in which case the two point sources cannot be resolved in the image. The Rayleigh criterion specifies that two point sources can be considered to be resolvable if the separation of the two images is at least the radius of the Airy disk, i.e. if the first minimum of one coincides with the maximum of the other.
Thus, the larger the aperture of the lens, and the smaller the wavelength, the finer the resolution of an imaging system. This is why telescopes have very large lenses or mirrors, and why optical microscopes are limited in the detail which they can see.
which is seen when using a laser pointer is another diffraction phenomenon. It is a result of the superpostion of many waves with different phases, which are produced when a laser beam illuminates a rough surface. They add together to give a resultant wave whose amplitude, and therefore intensity varies randomly.

where h is Planck's constant and p is the momentum
of the particle (mass × velocity for slow-moving particles).
For most macroscopic objects, this wavelength is so short that it is not meaningful to assign a wavelength to them. A sodium atom traveling at about 30,000 m/s would have a De Broglie wavelength of about 50 pico meters.
Because the wavelength for even the smallest of macroscopic objects is extremely small, diffraction of matter waves is only visible for small particles, like electrons, neutrons, atoms and small molecules. The short wavelength of these matter waves makes them ideally suited to study the atomic crystal structure of solids and large molecules like proteins.
Relatively larger molecules like buckyballs were also shown to diffract.

Diffraction from a three dimensional periodic structure such as atoms in a crystal is called Bragg diffraction.
It is similar to what occurs when waves are scattered from a diffraction grating. Bragg diffraction is a consequence of interference between waves reflecting from different crystal planes.
The condition of constructive interference is given by Bragg's law:

where
Bragg diffraction may be carried out using either light of very short wavelength like x-rays or matter waves like neutrons
(and electrons
) whose wavelength is on the order of (or much smaller than) the atomic spacing. The pattern produced gives information of the separations of crystallographic planes d, allowing one to deduce the crystal structure. Diffraction contrast, in electron microscope
s and x-topography devices
in particular, is also a powerful tool for examining individual defects and local strain fields in crystals.
The length over which the phase in a beam of light is correlated, is called the coherence length
. In order for interference to occur, the path length difference must be smaller than the coherence length. This is sometimes referred to as spectral coherence, as it is related to the presence of different frequency components in the wave. In the case of light emitted by an atomic transition
, the coherence length is related to the lifetime of the excited state from which the atom made its transition.
If waves are emitted from an extended source, this can lead to incoherence in the transversal direction. When looking at a cross section of a beam of light, the length over which the phase is correlated is called the transverse coherence length. In the case of Young's double slit experiment, this would mean that if the transverse coherence length is smaller than the spacing between the two slits, the resulting pattern on a screen would look like two single slit diffraction patterns.
In the case of particles like electrons, neutrons and atoms, the coherence length is related to the spatial extent of the wave function that describes the particle.
Francesco Maria Grimaldi
Francesco Maria Grimaldi was an Italian Jesuit priest, mathematician and physicist who taught at the Jesuit college in Bologna....
coined the word "diffraction" and was the first to record accurate observations of the phenomenon in 1665. In classical physics, the diffraction phenomenon is described as the apparent bending of waves around small obstacles and the spreading out of waves past small openings. Similar effects occur when light waves travel through a medium with a varying refractive index
Refractive index
In optics the refractive index or index of refraction of a substance or medium is a measure of the speed of light in that medium. It is expressed as a ratio of the speed of light in vacuum relative to that in the considered medium....
or a sound wave through one with varying acoustic impedance
Acoustic impedance
The acoustic impedance at a particular frequency indicates how much sound pressure is generated by a given air vibration at that frequency. The acoustic impedance Z is frequency dependent and is very useful, for example, for describing the behaviour of musical wind instruments...
. Diffraction occurs with all waves, including sound
Sound
Sound is a mechanical wave that is an oscillation of pressure transmitted through a solid, liquid, or gas, composed of frequencies within the range of hearing and of a level sufficiently strong to be heard, or the sensation stimulated in organs of hearing by such vibrations.-Propagation of...
waves, water
Water
Water is a chemical substance with the chemical formula H2O. A water molecule contains one oxygen and two hydrogen atoms connected by covalent bonds. Water is a liquid at ambient conditions, but it often co-exists on Earth with its solid state, ice, and gaseous state . Water also exists in a...
waves, and electromagnetic waves
Electromagnetic radiation
Electromagnetic radiation is a form of energy that exhibits wave-like behavior as it travels through space...
such as visible light
Visible spectrum
The visible spectrum is the portion of the electromagnetic spectrum that is visible to the human eye. Electromagnetic radiation in this range of wavelengths is called visible light or simply light. A typical human eye will respond to wavelengths from about 390 to 750 nm. In terms of...
, x-ray
X-ray
X-radiation is a form of electromagnetic radiation. X-rays have a wavelength in the range of 0.01 to 10 nanometers, corresponding to frequencies in the range 30 petahertz to 30 exahertz and energies in the range 120 eV to 120 keV. They are shorter in wavelength than UV rays and longer than gamma...
s and radio waves
Radio waves
Radio waves are a type of electromagnetic radiation with wavelengths in the electromagnetic spectrum longer than infrared light. Radio waves have frequencies from 300 GHz to as low as 3 kHz, and corresponding wavelengths from 1 millimeter to 100 kilometers. Like all other electromagnetic waves,...
. As physical objects have wave-like properties (at the atomic level), diffraction also occurs with matter and can be studied according to the principles of quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
.
Richard Feynman
Richard Feynman
Richard Phillips Feynman was an American physicist known for his work in the path integral formulation of quantum mechanics, the theory of quantum electrodynamics and the physics of the superfluidity of supercooled liquid helium, as well as in particle physics...
said that
- "no-one has ever been able to define the difference between interference and diffraction satisfactorily. It is just a question of usage, and there is no specific, important physical difference between them."
He suggested that when there are only a few sources, say two, we call it interference, as in Young's slits, but with a large number of sources, the process is labelled diffraction.
While diffraction occurs whenever propagating waves encounter such changes, its effects are generally most pronounced for waves where the wavelength
Wavelength
In physics, the wavelength of a sinusoidal wave is the spatial period of the wave—the distance over which the wave's shape repeats.It is usually determined by considering the distance between consecutive corresponding points of the same phase, such as crests, troughs, or zero crossings, and is a...
is roughly similar to the dimensions of the diffracting objects. If the obstructing object provides multiple, closely spaced openings, a complex pattern of varying intensity can result. This is due to the superposition, or interference, of different parts of a wave that traveled to the observer by different paths (see diffraction grating
Diffraction grating
In optics, a diffraction grating is an optical component with a periodic structure, which splits and diffracts light into several beams travelling in different directions. The directions of these beams depend on the spacing of the grating and the wavelength of the light so that the grating acts as...
).
The formalism of diffraction can also describe the way in which waves of finite extent propagate in free space. For example, the expanding profile of a laser beam, the beam shape of a radar antenna and the field of view of an ultrasonic transducer can all be analysed using diffraction equations.
Examples

Diffraction grating
In optics, a diffraction grating is an optical component with a periodic structure, which splits and diffracts light into several beams travelling in different directions. The directions of these beams depend on the spacing of the grating and the wavelength of the light so that the grating acts as...
to form the familiar rainbow pattern seen when looking at a disk. This principle can be extended to engineer a grating with a structure such that it will produce any diffraction pattern desired; the hologram
Holography
Holography is a technique that allows the light scattered from an object to be recorded and later reconstructed so that when an imaging system is placed in the reconstructed beam, an image of the object will be seen even when the object is no longer present...
on a credit card is an example. Diffraction in the atmosphere
Atmospheric diffraction
Atmospheric diffraction is manifested in the following principal ways:* Fourier optics is the bending of light rays in the atmosphere, which results in remarkable visual displays of astronomical objects, such as depictions on this page....
by small particles can cause a bright ring to be visible around a bright light source like the sun or the moon. A shadow of a solid object, using light from a compact source, shows small fringes near its edges. The speckle pattern
Speckle pattern
A speckle pattern is a random intensity pattern produced by the mutual interference of a set of wavefronts. This phenomenon has been investigated by scientists since the time of Newton, but speckles have come into prominence since the invention of the laser and have now found a variety of...
which is observed when laser light falls on an optically rough surface is also a diffraction phenomenon. All these effects are a consequence of the fact that light propagates as a wave
Wave
In physics, a wave is a disturbance that travels through space and time, accompanied by the transfer of energy.Waves travel and the wave motion transfers energy from one point to another, often with no permanent displacement of the particles of the medium—that is, with little or no associated mass...
.
Diffraction can occur with any kind of wave. Ocean waves diffract around jetties
Jetty
A jetty is any of a variety of structures used in river, dock, and maritime works that are generally carried out in pairs from river banks, or in continuation of river channels at their outlets into deep water; or out into docks, and outside their entrances; or for forming basins along the...
and other obstacles. Sound waves can diffract around objects, which is why one can still hear someone calling even when hiding behind a tree.
Diffraction can also be a concern in some technical applications; it sets a fundamental limit to the resolution of a camera, telescope, or microscope.
History

Francesco Maria Grimaldi
Francesco Maria Grimaldi was an Italian Jesuit priest, mathematician and physicist who taught at the Jesuit college in Bologna....
, who also coined the term diffraction, from the Latin diffringere, 'to break into pieces', referring to light breaking up into different directions. The results of Grimaldi's observations were published posthumously in 1665. Isaac Newton
Isaac Newton
Sir Isaac Newton PRS was an English physicist, mathematician, astronomer, natural philosopher, alchemist, and theologian, who has been "considered by many to be the greatest and most influential scientist who ever lived."...
studied these effects and attributed them to inflexion of light rays. James Gregory
James Gregory (astronomer and mathematician)
James Gregory FRS was a Scottish mathematician and astronomer. He described an early practical design for the reflecting telescope – the Gregorian telescope – and made advances in trigonometry, discovering infinite series representations for several trigonometric functions.- Biography :The...
(1638–1675) observed the diffraction patterns caused by a bird feather, which was effectively the first diffraction grating to be discovered. Thomas Young
Thomas Young (scientist)
Thomas Young was an English polymath. He is famous for having partly deciphered Egyptian hieroglyphics before Jean-François Champollion eventually expanded on his work...
performed a celebrated experiment in 1803 demonstrating interference from two closely spaced slits. Explaining his results by interference of the waves emanating from the two different slits, he deduced that light must propagate as waves. Augustin-Jean Fresnel
Augustin-Jean Fresnel
Augustin-Jean Fresnel , was a French engineer who contributed significantly to the establishment of the theory of wave optics. Fresnel studied the behaviour of light both theoretically and experimentally....
did more definitive studies and calculations of diffraction, made public in 1815 and 1818, and thereby gave great support to the wave theory of light that had been advanced by Christiaan Huygens and reinvigorated by Young, against Newton's particle theory.
Mechanism

Superposition principle
In physics and systems theory, the superposition principle , also known as superposition property, states that, for all linear systems, the net response at a given place and time caused by two or more stimuli is the sum of the responses which would have been caused by each stimulus individually...
. The propagation of a wave can be visualized by considering every point on a wavefront as a point source for a secondary spherical wave. The wave displacement at any subsequent point is the sum of these secondary waves. When waves are added together, their sum is determined by the relative phases as well as the amplitudes of the individual waves so that the summed amplitude of the waves can have any value between zero and the sum of the individual amplitudes. Hence, diffraction patterns usually have a series of maxima and minima.
There are various analytical models which allow the diffracted field to be calculated, including the Kirchhoff-Fresnel diffraction equation
Kirchhoff's diffraction formula
Kirchhoff's diffraction formula can be used to model the propagation of light in a wide range of configurations, either analytically or using numerical modelling. It gives an expression for the wave disturbance when a monochromatic spherical wave passes through an opening in an opaque screen...
which is derived from wave equation
Wave equation
The wave equation is an important second-order linear partial differential equation for the description of waves – as they occur in physics – such as sound waves, light waves and water waves. It arises in fields like acoustics, electromagnetics, and fluid dynamics...
, the Fraunhofer diffraction
Fraunhofer diffraction
In optics, the Fraunhofer diffraction equation is used to model the diffraction of waves when the diffraction pattern is viewed at a long distance from the diffracting object, and also when it is viewed at the focal plane of an imaging lens....
approximation of the Kirchhoff equation which applies to the far field and the Fresnel diffraction
Fresnel diffraction
In optics, the Fresnel diffraction equation for near-field diffraction, is an approximation of Kirchhoff-Fresnel diffraction that can be applied to the propagation of waves in the near field....
approximation which applies to the near field. Most configurations cannot be solved analytically, but can yield numerical solutions through finite element and boundary element methods.
It is possible to obtain a qualitative understanding of many diffraction phenomena by considering how the relative phases of the individual secondary wave sources vary, and in particular, the conditions in which the phase difference equals half a cycle in which case waves will cancel one another out.
The simplest descriptions of diffraction are those in which the situation can be reduced to a two-dimensional problem. For water waves, this is already the case; water waves propagate only on the surface of the water. For light, we can often neglect one direction if the diffracting object extends in that direction over a distance far greater than the wavelength. In the case of light shining through small circular holes we will have to take into account the full three dimensional nature of the problem.
Single-slit diffraction


A slit which is wider than a wavelength produces interference effects in the space downstream of the slit. These can be explained by assuming that the slit behaves as though it has a large number of point sources spaced evenly across the width of the slit. The analysis of this system is simplified if we consider light of a single wavelength. If the incident light is monochromatic, these sources all have the same phase. Light incident at a given point in the space downstream of the slit is made up of contributions from each of these point sources and if the relative phases of these contributions vary by 2π or more, we may expect to find minima and maxima in the diffracted light. Such phase differences are caused by differences in the path lengths over which contributing rays reach the point from the slit.
We can find the angle at which a first minimum is obtained in the diffracted light by the following reasoning. The light from a source located at the top edge of the slit interferes destructively with a source located at the middle of the slit, when the path difference between them is equal to λ/2. Similarly, the source just below the top of the slit will interfere destructively with the source located just below the middle of the slit at the same angle. We can continue this reasoning along the entire height of the slit to conclude that the condition for destructive interference for the entire slit is the same as the condition for destructive interference between two narrow slits a distance apart that is half the width of the slit. The path difference is given by
 so that the minimum intensity occurs at an angle θmin given by
so that the minimum intensity occurs at an angle θmin given by
where
- d is the width of the slit,
-
 is the angle of incidence at which the minimum intensity occurs, and
is the angle of incidence at which the minimum intensity occurs, and -
 is the wavelength of the light
is the wavelength of the light
A similar argument can be used to show that if we imagine the slit to be divided into four, six, eight parts, etc., minima are obtained at angles θn given by

where
- n is an integer other than zero.
There is no such simple argument to enable us to find the maxima of the diffraction pattern. The intensity profile can be calculated using the Fraunhofer diffraction
Fraunhofer diffraction
In optics, the Fraunhofer diffraction equation is used to model the diffraction of waves when the diffraction pattern is viewed at a long distance from the diffracting object, and also when it is viewed at the focal plane of an imaging lens....
equation as

where
-
 is the intensity at a given angle,
is the intensity at a given angle, -
 is the original intensity, and
is the original intensity, and - the sinc function is given by sinc(x) = sin(πx)/(πx) if x ≠ 0, and sinc(0) = 1
This analysis applies only to the far field, that is, at a distance much larger than the width of the slit.

Diffraction grating
A diffraction grating is an optical component with a regular pattern. The form of the light diffracted by a grating depends on the structure of the elements and the number of elements present, but all gratings have intensity maxima at angles θm which are given by the grating equation
where
- θi is the angle at which the light is incident,
- d is the separation of grating elements, and
- m is an integer which can be positive or negative.
The light diffracted by a grating is found by summing the light diffracted from each of the elements, and is essentially a convolution
Convolution
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
of diffraction and interference patterns.
The figure shows the light diffracted by 2-element and 5-element gratings where the grating spacings are the same; it can be seen that the maxima are in the same position, but the detailed structures of the intensities are different.

Circular aperture
The far-field diffraction of a plane wave incident on a circular aperture is often referred to as the Airy Disk. The variation in intensity with angle is given by
where a is the radius of the circular aperture, k is equal to 2π/λ and J1 is a Bessel function
Bessel function
In mathematics, Bessel functions, first defined by the mathematician Daniel Bernoulli and generalized by Friedrich Bessel, are canonical solutions y of Bessel's differential equation:...
. The smaller the aperture, the larger the spot size at a given distance, and the greater the divergence of the diffracted beams.
General aperture
The wave that emerges from a point source has amplitude at location r that is given by the solution of the frequency domain
at location r that is given by the solution of the frequency domainFrequency domain
In electronics, control systems engineering, and statistics, frequency domain is a term used to describe the domain for analysis of mathematical functions or signals with respect to frequency, rather than time....
wave equation
Wave equation
The wave equation is an important second-order linear partial differential equation for the description of waves – as they occur in physics – such as sound waves, light waves and water waves. It arises in fields like acoustics, electromagnetics, and fluid dynamics...
for a point source (The Helmholtz Equation
Helmholtz equation
The Helmholtz equation, named for Hermann von Helmholtz, is the elliptic partial differential equation\nabla^2 A + k^2 A = 0where ∇2 is the Laplacian, k is the wavenumber, and A is the amplitude.-Motivation and uses:...
),

where
 is the 3-dimensional delta function. The delta function has only radial dependence, so the Laplace operator
is the 3-dimensional delta function. The delta function has only radial dependence, so the Laplace operatorLaplace operator
In mathematics the Laplace operator or Laplacian is a differential operator given by the divergence of the gradient of a function on Euclidean space. It is usually denoted by the symbols ∇·∇, ∇2 or Δ...
(aka scalar Laplacian) in the spherical coordinate system
Spherical coordinate system
In mathematics, a spherical coordinate system is a coordinate system for three-dimensional space where the position of a point is specified by three numbers: the radial distance of that point from a fixed origin, its inclination angle measured from a fixed zenith direction, and the azimuth angle of...
simplifies to (see del in cylindrical and spherical coordinates
Del in cylindrical and spherical coordinates
This is a list of some vector calculus formulae of general use in working with various curvilinear coordinate systems.- Note :* This page uses standard physics notation. For spherical coordinates, \theta is the angle between the z axis and the radius vector connecting the origin to the point in...
)

By direct substitution, the solution to this equation can be readily shown to be the scalar Green's function
Green's function
In mathematics, a Green's function is a type of function used to solve inhomogeneous differential equations subject to specific initial conditions or boundary conditions...
, which in the spherical coordinate system
Spherical coordinate system
In mathematics, a spherical coordinate system is a coordinate system for three-dimensional space where the position of a point is specified by three numbers: the radial distance of that point from a fixed origin, its inclination angle measured from a fixed zenith direction, and the azimuth angle of...
(and using the physics time convention
 ) is:
) is:
This solution assumes that the delta function source is located at the origin. If the source is located at an arbitrary source point, denoted by the vector
 and the field point is located at the point
and the field point is located at the point  , then we may represent the scalar Green's function
, then we may represent the scalar Green's functionGreen's function
In mathematics, a Green's function is a type of function used to solve inhomogeneous differential equations subject to specific initial conditions or boundary conditions...
(for arbitrary source location) as:

Therefore, if an electric field, Einc(x,y) is incident on the aperture, the field produced by this aperture distribution is given by the surface integral
Surface integral
In mathematics, a surface integral is a definite integral taken over a surface ; it can be thought of as the double integral analog of the line integral...
:



In the far field, wherein the parallel rays approximation can be employed, the Green's function,

simplifies to

as can be seen in the figure to the right (click to enlarge).
The expression for the far-zone (Fraunhofer region) field becomes

Now, since

and

the expression for the Fraunhofer region field from a planar aperture now becomes,

Letting,

and

the Fraunhofer region field of the planar aperture assumes the form of a Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...

In the far-field / Fraunhofer region, this becomes the spatial Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
of the aperture distribution. Huygens' principle when applied to an aperture simply says that the far-field diffraction pattern is the spatial Fourier transform of the aperture shape, and this is a direct by-product of using the parallel-rays approximation, which is identical to doing a plane wave decomposition of the aperture plane fields (see Fourier optics
Fourier optics
Fourier optics is the study of classical optics using Fourier transforms and can be seen as the dual of the Huygens-Fresnel principle. In the latter case, the wave is regarded as a superposition of expanding spherical waves which radiate outward from actual current sources via a Green's function...
).
Propagation of a laser beam
The way in which the profileGaussian beam
In optics, a Gaussian beam is a beam of electromagnetic radiation whose transverse electric field and intensity distributions are well approximated by Gaussian functions. Many lasers emit beams that approximate a Gaussian profile, in which case the laser is said to be operating on the fundamental...
of a laser beam
Laser
A laser is a device that emits light through a process of optical amplification based on the stimulated emission of photons. The term "laser" originated as an acronym for Light Amplification by Stimulated Emission of Radiation...
changes as it propagates is determined by diffraction. The output mirror of the laser is an aperture, and the subsequent beam shape is determined by that aperture. Hence, the smaller the output beam, the quicker it diverges. Diode lasers have much greater divergence than He–Ne lasers for this reason.
Paradoxically, it is possible to reduce the divergence of a laser beam by first expanding it with one convex lens, and then collimating it with a second convex lens whose focal point is coincident with that of the first lens. The resulting beam has a larger aperture, and hence a lower divergence.
Diffraction-limited imaging

Diffraction-limited
The resolution of an optical imaging system — a microscope, telescope, or camera — can be limited by factors such as imperfections in the lenses or misalignment. However, there is a fundamental maximum to the resolution of any optical system which is due to diffraction...
. This is because a plane wave incident on a circular lens or mirror is diffracted as described above. The light is not focused to a point but forms an Airy disk having a central spot in the focal plane with radius to first null of

where λ is the wavelength of the light and N is the f-number
F-number
In optics, the f-number of an optical system expresses the diameter of the entrance pupil in terms of the focal length of the lens; in simpler terms, the f-number is the focal length divided by the "effective" aperture diameter...
(focal length divided by diameter) of the imaging optics. In object space, the corresponding angular resolution
Angular resolution
Angular resolution, or spatial resolution, describes the ability of any image-forming device such as an optical or radio telescope, a microscope, a camera, or an eye, to distinguish small details of an object...
is

where D is the diameter of the entrance pupil
Entrance pupil
In an optical system, the entrance pupil is the optical image of the physical aperture stop, as 'seen' through the front of the lens system. The corresponding image of the aperture as seen through the back of the lens system is called the exit pupil...
of the imaging lens (e.g., of a telescope's main mirror).
Two point sources will each produce an Airy pattern – see the photo of a binary star. As the point sources move closer together, the patterns will start to overlap, and ultimately they will merge to form a single pattern, in which case the two point sources cannot be resolved in the image. The Rayleigh criterion specifies that two point sources can be considered to be resolvable if the separation of the two images is at least the radius of the Airy disk, i.e. if the first minimum of one coincides with the maximum of the other.
Thus, the larger the aperture of the lens, and the smaller the wavelength, the finer the resolution of an imaging system. This is why telescopes have very large lenses or mirrors, and why optical microscopes are limited in the detail which they can see.
Speckle patterns
The speckle patternSpeckle pattern
A speckle pattern is a random intensity pattern produced by the mutual interference of a set of wavefronts. This phenomenon has been investigated by scientists since the time of Newton, but speckles have come into prominence since the invention of the laser and have now found a variety of...
which is seen when using a laser pointer is another diffraction phenomenon. It is a result of the superpostion of many waves with different phases, which are produced when a laser beam illuminates a rough surface. They add together to give a resultant wave whose amplitude, and therefore intensity varies randomly.
Patterns
Several qualitative observations can be made of diffraction in general:- The angular spacing of the features in the diffraction pattern is inversely proportional to the dimensions of the object causing the diffraction. In other words: The smaller the diffracting object, the 'wider' the resulting diffraction pattern, and vice versa. (More precisely, this is true of the sineSineIn mathematics, the sine function is a function of an angle. In a right triangle, sine gives the ratio of the length of the side opposite to an angle to the length of the hypotenuse.Sine is usually listed first amongst the trigonometric functions....
s of the angles.) - The diffraction angles are invariant under scaling; that is, they depend only on the ratio of the wavelength to the size of the diffracting object.
- When the diffracting object has a periodic structure, for example in a diffraction grating, the features generally become sharper. The third figure, for example, shows a comparison of a double-slitDouble-slit experimentThe double-slit experiment, sometimes called Young's experiment, is a demonstration that matter and energy can display characteristics of both waves and particles...
pattern with a pattern formed by five slits, both sets of slits having the same spacing, between the center of one slit and the next.
Particle diffraction
Quantum theory tells us that every particle exhibits wave properties. In particular, massive particles can interfere and therefore diffract. Diffraction of electrons and neutrons stood as one of the powerful arguments in favor of quantum mechanics. The wavelength associated with a particle is the de Broglie wavelength
where h is Planck's constant and p is the momentum
Momentum
In classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...
of the particle (mass × velocity for slow-moving particles).
For most macroscopic objects, this wavelength is so short that it is not meaningful to assign a wavelength to them. A sodium atom traveling at about 30,000 m/s would have a De Broglie wavelength of about 50 pico meters.
Because the wavelength for even the smallest of macroscopic objects is extremely small, diffraction of matter waves is only visible for small particles, like electrons, neutrons, atoms and small molecules. The short wavelength of these matter waves makes them ideally suited to study the atomic crystal structure of solids and large molecules like proteins.
Relatively larger molecules like buckyballs were also shown to diffract.
Bragg diffraction

Diffraction from a three dimensional periodic structure such as atoms in a crystal is called Bragg diffraction.
It is similar to what occurs when waves are scattered from a diffraction grating. Bragg diffraction is a consequence of interference between waves reflecting from different crystal planes.
The condition of constructive interference is given by Bragg's law:

where
- λ is the wavelength,
- d is the distance between crystal planes,
- θ is the angle of the diffracted wave.
- and m is an integer known as the order of the diffracted beam.
Bragg diffraction may be carried out using either light of very short wavelength like x-rays or matter waves like neutrons
Neutron diffraction
Neutron diffraction or elastic neutron scattering is the application of neutron scattering to the determination of the atomic and/or magnetic structure of a material: A sample to be examined is placed in a beam of thermal or cold neutrons to obtain a diffraction pattern that provides information of...
(and electrons
Electron diffraction
Electron diffraction refers to the wave nature of electrons. However, from a technical or practical point of view, it may be regarded as a technique used to study matter by firing electrons at a sample and observing the resulting interference pattern...
) whose wavelength is on the order of (or much smaller than) the atomic spacing. The pattern produced gives information of the separations of crystallographic planes d, allowing one to deduce the crystal structure. Diffraction contrast, in electron microscope
Electron microscope
An electron microscope is a type of microscope that uses a beam of electrons to illuminate the specimen and produce a magnified image. Electron microscopes have a greater resolving power than a light-powered optical microscope, because electrons have wavelengths about 100,000 times shorter than...
s and x-topography devices
Diffraction topography
Diffraction topography is an X-ray imaging technique based on Bragg diffraction.Diffraction topographic images record the intensity profile of a beam of X-rays diffracted by a crystal....
in particular, is also a powerful tool for examining individual defects and local strain fields in crystals.
Coherence
The description of diffraction relies on the interference of waves emanating from the same source taking different paths to the same point on a screen. In this description, the difference in phase between waves that took different paths is only dependent on the effective path length. This does not take into account the fact that waves that arrive at the screen at the same time were emitted by the source at different times. The initial phase with which the source emits waves can change over time in an unpredictable way. This means that waves emitted by the source at times that are too far apart can no longer form a constant interference pattern since the relation between their phases is no longer time independent.The length over which the phase in a beam of light is correlated, is called the coherence length
Coherence length
In physics, coherence length is the propagation distance from a coherent source to a point where an electromagnetic wave maintains a specified degree of coherence. The significance is that interference will be strong within a coherence length of the source, but not beyond it...
. In order for interference to occur, the path length difference must be smaller than the coherence length. This is sometimes referred to as spectral coherence, as it is related to the presence of different frequency components in the wave. In the case of light emitted by an atomic transition
Energy level
A quantum mechanical system or particle that is bound -- that is, confined spatially—can only take on certain discrete values of energy. This contrasts with classical particles, which can have any energy. These discrete values are called energy levels...
, the coherence length is related to the lifetime of the excited state from which the atom made its transition.
If waves are emitted from an extended source, this can lead to incoherence in the transversal direction. When looking at a cross section of a beam of light, the length over which the phase is correlated is called the transverse coherence length. In the case of Young's double slit experiment, this would mean that if the transverse coherence length is smaller than the spacing between the two slits, the resulting pattern on a screen would look like two single slit diffraction patterns.
In the case of particles like electrons, neutrons and atoms, the coherence length is related to the spatial extent of the wave function that describes the particle.
See also
- Atmospheric diffractionAtmospheric diffractionAtmospheric diffraction is manifested in the following principal ways:* Fourier optics is the bending of light rays in the atmosphere, which results in remarkable visual displays of astronomical objects, such as depictions on this page....
- Bragg diffraction
- Brocken spectreBrocken spectreA Brocken spectre , also called Brocken bow, mountain spectre or glockenspectre is the apparently enormous and magnified shadow of an observer, cast upon the upper surfaces of clouds opposite the sun...
- Cloud iridescenceCloud iridescencethumb|260px|Cloud iridescenceCloud iridescence is the occurrence of colors in a cloud similar to those seen in oil films on puddles, and is similar to irisation. It is a fairly uncommon phenomenon, most often observed in altocumulus, cirrocumulus and lenticular clouds, and very rarely in Cirrus...
- Diffraction formalismDiffraction formalism- Quantitative description and analysis :Because diffraction is the result of addition of all waves along all unobstructed paths, the usual procedure is to consider the contribution of an infinitesimally small neighborhood around a certain path and then integrate over all paths from the source...
- Diffraction gratingDiffraction gratingIn optics, a diffraction grating is an optical component with a periodic structure, which splits and diffracts light into several beams travelling in different directions. The directions of these beams depend on the spacing of the grating and the wavelength of the light so that the grating acts as...
- Diffraction limit
- DiffractometerDiffractometerA diffractometer is a measuring instrument for analyzing the structure of a material from the scattering pattern produced when a beam of radiation or particles interacts with it....
- Dynamical theory of diffractionDynamical theory of diffractionThe dynamical theory of diffraction describes the interaction of waves with a regular lattice. The wave fields traditionally described are X-rays, neutrons or electrons and the regular lattice, atomic crystal structures or nanometer scaled multi-layers or self arranged systems...
- Electron diffractionElectron diffractionElectron diffraction refers to the wave nature of electrons. However, from a technical or practical point of view, it may be regarded as a technique used to study matter by firing electrons at a sample and observing the resulting interference pattern...
- Fraunhofer diffractionFraunhofer diffractionIn optics, the Fraunhofer diffraction equation is used to model the diffraction of waves when the diffraction pattern is viewed at a long distance from the diffracting object, and also when it is viewed at the focal plane of an imaging lens....
- Fresnel diffractionFresnel diffractionIn optics, the Fresnel diffraction equation for near-field diffraction, is an approximation of Kirchhoff-Fresnel diffraction that can be applied to the propagation of waves in the near field....
- Fresnel imagerFresnel ImagerA Fresnel imager is a proposed ultra-lightweight design for a space telescope that uses a Fresnel array as primary optics instead of a typical lens. It focuses light with a thin opaque foil sheet punched with specially shaped holes, thus focusing light on a certain point by using the phenomenon of...
- Fresnel numberFresnel numberThe Fresnel number F, named after the physicist Augustin-Jean Fresnel, is a dimensionless number occurring in optics, in particular in diffraction theory....
- Fresnel zoneFresnel zoneIn optics and radio communications , a Fresnel zone , named for physicist Augustin-Jean Fresnel, is one of a number of concentric ellipsoids which define volumes in the radiation pattern of a circular aperture...
- Neutron diffractionNeutron diffractionNeutron diffraction or elastic neutron scattering is the application of neutron scattering to the determination of the atomic and/or magnetic structure of a material: A sample to be examined is placed in a beam of thermal or cold neutrons to obtain a diffraction pattern that provides information of...
- PrismPrism (optics)In optics, a prism is a transparent optical element with flat, polished surfaces that refract light. The exact angles between the surfaces depend on the application. The traditional geometrical shape is that of a triangular prism with a triangular base and rectangular sides, and in colloquial use...
- Powder diffractionPowder diffractionPowder diffraction is a scientific technique using X-ray, neutron, or electron diffraction on powder or microcrystalline samples for structural characterization of materials.-Explanation:...
- RefractionRefractionRefraction is the change in direction of a wave due to a change in its speed. It is essentially a surface phenomenon . The phenomenon is mainly in governance to the law of conservation of energy. The proper explanation would be that due to change of medium, the phase velocity of the wave is changed...
- Schaefer–Bergmann diffraction
- Thinned array curseThinned array curseThe thinned array curse is a theorem in electromagnetic theory of transmitters. It states that a transmitting aperture which is synthesized by a coherent phased array of smaller apertures that are spaced apart will have a smaller minimum beam spot size The thinned array curse (sometimes, sparse...
- X-ray scattering techniquesX-ray scattering techniquesX-ray scattering techniques are a family of non-destructive analytical techniques which reveal information about the crystallographic structure, chemical composition, and physical properties of materials and thin films...
External links
- Diffraction and Crystallography for beginners
- Do Sensors “Outresolve” Lenses?; on lens and sensor resolution interaction.
- Diffraction and acoustics.
- Diffraction in photography.
- On Diffraction at MathPages.
- Diffraction pattern calculators at The Wolfram Demonstrations Project
- Wave Optics – A chapter of an online textbook.
- 2-D wave Java applet – Displays diffraction patterns of various slit configurations.
- Diffraction Java applet – Displays diffraction patterns of various 2-D apertures.
- Diffraction approximations illustrated – MIT site that illustrates the various approximations in diffraction and intuitively explains the Fraunhofer regime from the perspective of linear system theory.
- Gap Obstacle Corner – Java simulation of diffraction of water wave.
- Google Maps – Satellite image of Panama Canal entry ocean wave diffraction.
- Google Maps and Bing Maps - Aerial photo of waves diffracting through sea barriers at Sea PallingSea PallingSea Palling is a village and a civil parish covering in the English county of Norfolk. The village is south-east of Cromer, north-east of Norwich and north-east of London. The village lies east of the A149 between Kings Lynn and Great Yarmouth...
in NorfolkNorfolkNorfolk is a low-lying county in the East of England. It has borders with Lincolnshire to the west, Cambridgeshire to the west and southwest and Suffolk to the south. Its northern and eastern boundaries are the North Sea coast and to the north-west the county is bordered by The Wash. The county...
, UK. - Diffraction Effects
- An Introduction to The Wigner Distribution in Geometric Optics
- DoITPoMS Teaching and Learning Package - Diffraction and Imaging

