
Damping
Encyclopedia

In physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, damping is any effect that tends to reduce the amplitude
Amplitude
Amplitude is the magnitude of change in the oscillating variable with each oscillation within an oscillating system. For example, sound waves in air are oscillations in atmospheric pressure and their amplitudes are proportional to the change in pressure during one oscillation...
of oscillation
Oscillation
Oscillation is the repetitive variation, typically in time, of some measure about a central value or between two or more different states. Familiar examples include a swinging pendulum and AC power. The term vibration is sometimes used more narrowly to mean a mechanical oscillation but sometimes...
s in an oscillatory system, particularly the harmonic oscillator
Harmonic oscillator
In classical mechanics, a harmonic oscillator is a system that, when displaced from its equilibrium position, experiences a restoring force, F, proportional to the displacement, x: \vec F = -k \vec x \, where k is a positive constant....
.
In mechanics
Mechanics
Mechanics is the branch of physics concerned with the behavior of physical bodies when subjected to forces or displacements, and the subsequent effects of the bodies on their environment....
, friction is one such damping effect. For many purposes the frictional force Ff can be modeled as being proportional to the velocity v of the object:

where c is the viscous damping coefficient, given in units of newton seconds per meter (N s/m) or simply kilograms per second.
Generally, damped harmonic oscillators satisfy the second-order differential equation
Ordinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
:

where ω0 is the undamped angular frequency
Angular frequency
In physics, angular frequency ω is a scalar measure of rotation rate. Angular frequency is the magnitude of the vector quantity angular velocity...
of the oscillator and ζ is a constant called the damping ratio
Damping ratio
[[Image:Damped spring.gif|right|frame|Underdamped [[spring–mass system]] with ζ 1 , and is referred to as overdamped.*Underdamped:If s is a complex number, then the solution is a decaying exponential combined with an oscillatory portion that looks like \exp...
.
The value of the damping ratio ζ determines the behavior of the system. A damped harmonic oscillator can be:
- Overdamped (ζ > 1): The system returns (exponentially decays) to equilibrium without oscillating. Larger values of the damping ratio ζ return to equilibrium slower.
- Critically damped (ζ = 1): The system returns to equilibrium as quickly as possible without oscillating. This is often desired for the damping of systems such as doors.
- Underdamped (0 < ζ < 1): The system oscillates (at reduced frequency compared to the undamped case) with the amplitude gradually decreasing to zero.
- Undamped (ζ = 0): The system oscillates at its natural resonant frequency (ωo).
Definition
In physicsPhysics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
and engineering
Engineering
Engineering is the discipline, art, skill and profession of acquiring and applying scientific, mathematical, economic, social, and practical knowledge, in order to design and build structures, machines, devices, systems, materials and processes that safely realize improvements to the lives of...
, damping may be mathematically modelled
Mathematical model
A mathematical model is a description of a system using mathematical concepts and language. The process of developing a mathematical model is termed mathematical modeling. Mathematical models are used not only in the natural sciences and engineering disciplines A mathematical model is a...
as a force
Force
In physics, a force is any influence that causes an object to undergo a change in speed, a change in direction, or a change in shape. In other words, a force is that which can cause an object with mass to change its velocity , i.e., to accelerate, or which can cause a flexible object to deform...
synchronous with the velocity
Velocity
In physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...
of the object but opposite in direction to it. If such force is also proportional to the velocity, as for a simple mechanical viscous damper (dashpot), the force F may be related to the velocity v by

where c is the viscous damping coefficient, given in units of newton-seconds per meter.
This force is an approximation to the friction
Friction
Friction is the force resisting the relative motion of solid surfaces, fluid layers, and/or material elements sliding against each other. There are several types of friction:...
caused by drag
Drag (physics)
In fluid dynamics, drag refers to forces which act on a solid object in the direction of the relative fluid flow velocity...
.
This relationship is perfectly analogous to electrical resistance
Electrical resistance
The electrical resistance of an electrical element is the opposition to the passage of an electric current through that element; the inverse quantity is electrical conductance, the ease at which an electric current passes. Electrical resistance shares some conceptual parallels with the mechanical...
as described by Ohm's law
Ohm's law
Ohm's law states that the current through a conductor between two points is directly proportional to the potential difference across the two points...
.
Example: mass–spring–damper
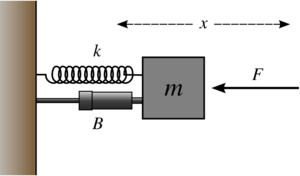
Hooke's law
In mechanics, and physics, Hooke's law of elasticity is an approximation that states that the extension of a spring is in direct proportion with the load applied to it. Many materials obey this law as long as the load does not exceed the material's elastic limit. Materials for which Hooke's law...
–damper system with mass m, spring constant k and viscous damper of damping coefficient c is subject to an oscillatory force
and a damping force

The values can be in any consistent system of units; for example, in SI units, m in kilograms, k in newtons per meter, and c in newton-second
Newton-second
The newton-second or newton second is the derived SI unit of impulse and momentum. It can also be expressed as the kilogram metre per second...
s per meter or kilograms per second
Second
The second is a unit of measurement of time, and is the International System of Units base unit of time. It may be measured using a clock....
.
Treating the mass as a free body
Free body
Free body is the generic term used by physicists and engineers to describe an object—be it a bowling ball, a spacecraft, pendulum, a television, or anything else—which can be considered as moving as a single unit. The object doesn't have to be "free" in the usual sense of the...
and applying Newton's second law, the total force Ftot on the body is

where a is the acceleration
Acceleration
In physics, acceleration is the rate of change of velocity with time. In one dimension, acceleration is the rate at which something speeds up or slows down. However, since velocity is a vector, acceleration describes the rate of change of both the magnitude and the direction of velocity. ...
of the mass and x is the displacement
Displacement (vector)
A displacement is the shortest distance from the initial to the final position of a point P. Thus, it is the length of an imaginary straight path, typically distinct from the path actually travelled by P...
of the mass relative to a fixed point of reference.
Since Ftot = Fs + Fd,

This differential equation may be rearranged into
The following parameters are then defined:
The first parameter, ω0, is called the (undamped) natural frequency
Resonance
In physics, resonance is the tendency of a system to oscillate at a greater amplitude at some frequencies than at others. These are known as the system's resonant frequencies...
of the system .
The second parameter, ζ, is called the damping ratio
Damping ratio
[[Image:Damped spring.gif|right|frame|Underdamped [[spring–mass system]] with ζ 1 , and is referred to as overdamped.*Underdamped:If s is a complex number, then the solution is a decaying exponential combined with an oscillatory portion that looks like \exp...
. The
natural frequency represents an angular frequency
Angular frequency
In physics, angular frequency ω is a scalar measure of rotation rate. Angular frequency is the magnitude of the vector quantity angular velocity...
, expressed in radian
Radian
Radian is the ratio between the length of an arc and its radius. The radian is the standard unit of angular measure, used in many areas of mathematics. The unit was formerly a SI supplementary unit, but this category was abolished in 1995 and the radian is now considered a SI derived unit...
s per second. The damping ratio is a dimensionless quantity
Dimensionless quantity
In dimensional analysis, a dimensionless quantity or quantity of dimension one is a quantity without an associated physical dimension. It is thus a "pure" number, and as such always has a dimension of 1. Dimensionless quantities are widely used in mathematics, physics, engineering, economics, and...
.
The differential equation now becomes

Continuing, we can solve the equation by assuming a solution x such that:

where the parameter
Parameter
Parameter from Ancient Greek παρά also “para” meaning “beside, subsidiary” and μέτρον also “metron” meaning “measure”, can be interpreted in mathematics, logic, linguistics, environmental science and other disciplines....
γ (gamma
Gamma
Gamma is the third letter of the Greek alphabet. In the system of Greek numerals it has a value of 3. It was derived from the Phoenician letter Gimel . Letters that arose from Gamma include the Roman C and G and the Cyrillic letters Ge Г and Ghe Ґ.-Greek:In Ancient Greek, gamma represented a...
) is, in general, a complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
.
Substituting this assumed solution back into the differential equation gives

which is the characteristic equation.
Solving the characteristic equation will give two roots, γ+ and γ−. The solution to the differential equation is thus
-

where A and B are determined by the initial conditions of the system:
-

-

System behavior
The behavior of the system depends on the relative values of the two fundamental parameters, the natural frequency ω0 and the damping ratio ζ. In particular, the qualitative behavior of the system depends crucially on whether the quadratic equationQuadratic equationIn mathematics, a quadratic equation is a univariate polynomial equation of the second degree. A general quadratic equation can be written in the formax^2+bx+c=0,\,...
for γ has one real solution, two real solutions, or two complex conjugate solutions.
Critical damping (ζ = 1)
When , there is a double root γ (defined above), which is real. The system is said to be critically damped. A critically damped system converges to zero as fast as possible without oscillating. An example of critical damping is the door closerDoor closerA door closer is a mechanical device that closes a door, in general after someone opens it, or after it was automatically opened. Choosing a door closer can involve the consideration of a variety of criteria...
seen on many hinged doors in public buildings. The recoil mechanisms in most guns are also critically damped so that they return to their original position, after the recoil due to firing, in the least possible time.
In this case, with only one root γ, there is in addition to the solution a solution :
-

where and
and  are determined by the initial conditions of the system (usually the initial position and velocity of the mass):
are determined by the initial conditions of the system (usually the initial position and velocity of the mass):
-

-

Over-damping (ζ > 1)
When ζ > 1, the system is over-damped and there are two different real roots. An over-damped door-closer will take longer to close than a critically damped door would.
The solution to the motion equation is:
-

where and
and  are determined by the initial conditions of the system:
are determined by the initial conditions of the system:
-

-

Under-damping (0 ≤ ζ < 1)
Finally, when 0 ≤ ζ < 1, γ is complexComplex numberA complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
, and the system is under-damped. In this situation, the system will oscillate at the natural damped frequency ωd, which is a function of the natural frequency and the damping ratio. To continue the analogy, an underdamped door closer would close quickly, but would hit the door frame with significant velocity, or would oscillate in the case of a swinging door.
In this case, the solution can be generally written as:

where
represents the damped frequency or ringing frequency of the system,
and A and B are again determined by the initial conditions of the system:
This "damped frequency" is not to be confused with the damped resonant frequency or peak frequency ωpeak.
This is the frequency at which a moderately underdamped (ζ < 1/) simple 2nd-order harmonic oscillator has its maximum gain (or peak transmissibility) when driven by a sinusoidalSine waveThe sine wave or sinusoid is a mathematical function that describes a smooth repetitive oscillation. It occurs often in pure mathematics, as well as physics, signal processing, electrical engineering and many other fields...
input. The frequency at which this peak occurs is given by:
For an under-damped system, the value of ζ can be found by examining the logarithm of the ratio of succeeding amplitudes of a system. This is called the logarithmic decrementLogarithmic decrementLogarithmic decrement, δ, is used to find the damping ratio of an underdamped system in the time domain. The logarithmic decrement is the natural log of the ratio of the amplitudes of any two successive peaks:...
.
Alternative models
Viscous damping models, although widely used, are not the only damping models. A wide range of models can be found in specialized literature. One is the so called "hysteretic damping model" or "structural damping model".
When a metal beam is vibrating, the internal damping can be better described by a force proportional to the displacement but in phase with the velocity. In such case, the differential equationDifferential equationA differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
that describes the free movement of a single-degree-of-freedom system becomes:
-

where h is the hysteretic damping coefficient and i denotes the imaginary unitImaginary unitIn mathematics, the imaginary unit allows the real number system ℝ to be extended to the complex number system ℂ, which in turn provides at least one root for every polynomial . The imaginary unit is denoted by , , or the Greek...
; the presence of i is required to synchronize the damping force to the velocity (xi being in phase with the velocity).
This equation is more often written as:
-

where η is the hysteretic damping ratio, that is, the fraction of energy lost in each cycle of the vibration.
Although requiring complex analysisComplex analysisComplex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
to solve the equation, this model reproduces the real behaviour of many vibrating structures more closely than the viscous model.
A more general model that also requires complex analysis, the fractional model not only includes both the viscous and hysteretic models, but also allows for intermediate cases (useful for some polymers):
-

where r is any number, usually between 0 (for hysteretic) and 1 (for viscous), and A is a general damping (h for hysteretic and c for viscous) coefficient.
Books
Komkov, VadimVadim KomkovVadim Komkov obtained a Ph.D. from the University of Utah in 1965. He was a professor of Mathematics at Texas Tech University from 1969-1980. He also taught at the University of Utah, the University of Wisconsin, Florida State University, West Virginia University, and Winthrop University in...
(1972) Optimal control theory for the damping of vibrations of simple elastic systems. Lecture Notes in Mathematics, Vol. 253. Springer-Verlag, Berlin-New York.
External links
-
-
-
-
-
-
-
-
-
-
-







