In fluid dynamics

Fluid dynamics

In physics, fluid dynamics is a sub-discipline of fluid mechanics that deals with fluid flow—the natural science of fluids in motion. It has several subdisciplines itself, including aerodynamics and hydrodynamics...

, the Ursell number indicates the nonlinearity

Nonlinearity

In mathematics, a nonlinear system is one that does not satisfy the superposition principle, or one whose output is not directly proportional to its input; a linear system fulfills these conditions. In other words, a nonlinear system is any problem where the variable to be solved for cannot be...

 of long surface gravity waves

Ocean surface wave

In fluid dynamics, wind waves or, more precisely, wind-generated waves are surface waves that occur on the free surface of oceans, seas, lakes, rivers, and canals or even on small puddles and ponds. They usually result from the wind blowing over a vast enough stretch of fluid surface. Waves in the...

 on a fluid

Fluid

In physics, a fluid is a substance that continually deforms under an applied shear stress. Fluids are a subset of the phases of matter and include liquids, gases, plasmas and, to some extent, plastic solids....

 layer. This dimensionless parameter is named after Fritz Ursell

Fritz Ursell

Fritz Joseph Ursell FRS is a British mathematician noted for his contributions to fluid mechanics, especially in the area of wave-structure interactions. He held the Beyer Chair of Applied Mathematics at the University of Manchester from 1961–1990, was elected Fellow of the Royal Society in 1972...

, who discussed its significance in 1953.

The Ursell number is derived from the Stokes' perturbation series

Perturbation theory

Perturbation theory comprises mathematical methods that are used to find an approximate solution to a problem which cannot be solved exactly, by starting from the exact solution of a related problem...

 for nonlinear periodic

Periodic function

In mathematics, a periodic function is a function that repeats its values in regular intervals or periods. The most important examples are the trigonometric functions, which repeat over intervals of length 2π radians. Periodic functions are used throughout science to describe oscillations,...

 waves, in the long-wave limit

Limit (mathematics)

In mathematics, the concept of a "limit" is used to describe the value that a function or sequence "approaches" as the input or index approaches some value. The concept of limit allows mathematicians to define a new point from a Cauchy sequence of previously defined points within a complete metric...

 of shallow water

Waves and shallow water

When waves travel into areas of shallow water, they begin to be affected by the ocean bottom. The free orbital motion of the water is disrupted, and water particles in orbital motion no longer return to their original position. As the water becomes shallower, the swell becomes higher and steeper,...

 — when the wavelength

Wavelength

In physics, the wavelength of a sinusoidal wave is the spatial period of the wave—the distance over which the wave's shape repeats.It is usually determined by considering the distance between consecutive corresponding points of the same phase, such as crests, troughs, or zero crossings, and is a...

 is much larger than the water depth. Then the Ursell number U is defined as:


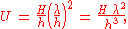
which is, apart from a constant 3 / (32 π²), the ratio of the amplitude

Amplitude

Amplitude is the magnitude of change in the oscillating variable with each oscillation within an oscillating system. For example, sound waves in air are oscillations in atmospheric pressure and their amplitudes are proportional to the change in pressure during one oscillation...

s of the second-order to the first-order term in the free surface

Free surface

In physics, a free surface is the surface of a fluid that is subject to constant perpendicular normal stress and zero parallel shear stress,such as the boundary between two homogenous fluids,for example liquid water and the air in the Earth's atmosphere...

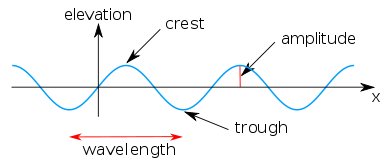
 elevation.
The used parameters are:

• H : the wave height
  Wave height
  In fluid dynamics, the wave height of a surface wave is the difference between the elevations of a crest and a neighbouring trough. Wave height is a term used by mariners, as well as in coastal, ocean and naval engineering....
  
  , i.e. the difference between the elevations of the wave crest
  Crest (physics)
  A crest is the point on a wave with the maximum value or upward displacement within a cycle. A trough is the opposite of a crest, so the minimum or lowest point in a cycle.-Interference:...
  
   and trough,
• h : the mean water depth, and
• λ : the wavelength, which has to be large compared to the depth, λ ≫ h.

So the Ursell parameter U is the relative wave height H / h times the relative wavelength λ / h squared.

For long waves (λ ≫ h) with small Ursell number, U ≪ 32 π² / 3 ≈ 100, linear wave theory is applicable. Otherwise (and most often) a non-linear theory for fairly long waves (λ > 7 h) — like the Korteweg–de Vries equation

Korteweg–de Vries equation

In mathematics, the Korteweg–de Vries equation is a mathematical model of waves on shallow water surfaces. It is particularly notable as the prototypical example of an exactly solvable model, that is, a non-linear partial differential equation whose solutions can be exactly and precisely specified...

 or Boussinesq equations

Boussinesq approximation (water waves)

In fluid dynamics, the Boussinesq approximation for water waves is an approximation valid for weakly non-linear and fairly long waves. The approximation is named after Joseph Boussinesq, who first derived them in response to the observation by John Scott Russell of the wave of translation...

 — has to be used.
The parameter, with different normalisation, was already introduced by George Gabriel Stokes

George Gabriel Stokes

Sir George Gabriel Stokes, 1st Baronet FRS , was an Irish mathematician and physicist, who at Cambridge made important contributions to fluid dynamics , optics, and mathematical physics...

in his historical paper on surface gravity waves of 1847.