.gif)
Strain (materials science)
Encyclopedia
In continuum mechanics
, the infinitesimal
strain theory, sometimes called small deformation theory, small displacement theory, or small displacement-gradient theory, deals with infinitesimal deformation
s of a continuum body
. For an infinitesimal deformation the displacements and the displacement gradients
and the displacement gradients  are small compared to unity, i.e.,
are small compared to unity, i.e.,  and
and  , allowing for the geometric linearisation of the Lagrangian finite strain tensor
, allowing for the geometric linearisation of the Lagrangian finite strain tensor  , and the Eulerian finite strain tensor
, and the Eulerian finite strain tensor  , i.e. the non-linear or second-order terms of the finite strain tensor can be neglected. The linearised Lagrangian and Eulerian strain tensors are approximately the same and can be approximated by the infinitesimal strain tensor or Cauchy's strain tensor,
, i.e. the non-linear or second-order terms of the finite strain tensor can be neglected. The linearised Lagrangian and Eulerian strain tensors are approximately the same and can be approximated by the infinitesimal strain tensor or Cauchy's strain tensor, 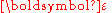 . Thus,
. Thus,
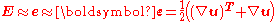
or
The infinitesimal strain theory is used in the analysis of deformations of materials exhibiting elastic
behaviour, such as materials found in mechanical and civil engineering applications, e.g. concrete and steel.
, in which the displacements and the displacement gradients are small compared to unity, i.e., and
and  , it is possible to perform a geometric linearisation of the Lagrangian finite strain tensor
, it is possible to perform a geometric linearisation of the Lagrangian finite strain tensor  , and the Eulerian finite strain tensor
, and the Eulerian finite strain tensor  . In such a linearisation, the non-linear or second-order terms of the finite strain tensor are neglected. Thus we have
. In such a linearisation, the non-linear or second-order terms of the finite strain tensor are neglected. Thus we have

or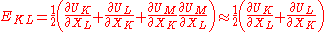
and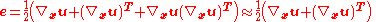
or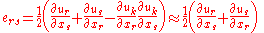
This linearisation implies that the Lagrangian description and the Eulerian description are approximately the same as there is little difference in the material and spatial coordinates of a given material point in the continuum. Therefore, the material displacement gradient components and the spatial displacement gradient components are approximately equal. Thus we have
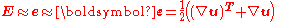
or

where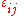 are the components of the infinitesimal strain tensor
are the components of the infinitesimal strain tensor 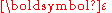 , also called Cauchy's strain tensor, linear strain tensor, or small strain tensor.
, also called Cauchy's strain tensor, linear strain tensor, or small strain tensor.

or using different notation:
Furthermore, since the deformation gradient can be expressed as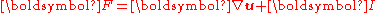 where
where  is the second-order identity tensor, we have
is the second-order identity tensor, we have

Also, from the general expression for the Lagrangian and Eulerian finite strain tensors we have

 Considering a two-dimensional deformation of an infinitesimal rectangular material element with dimensions
Considering a two-dimensional deformation of an infinitesimal rectangular material element with dimensions  by
by 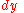 (Figure 1), which after deformation, takes the form of a rhombus. From the geometry of Figure 1 we have
(Figure 1), which after deformation, takes the form of a rhombus. From the geometry of Figure 1 we have
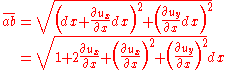
For very small displacement gradients, i.e., , we have
, we have
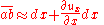
The normal strain in the -direction of the rectangular element is defined by
-direction of the rectangular element is defined by
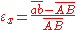
and knowing that , we have
, we have
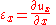
Similarly, the normal strain in the -direction, and
-direction, and  -direction, becomes
-direction, becomes
The engineering shear strain, or the change in angle between two originally orthogonal material lines, in this case line and
and  , is defined as
, is defined as
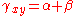
From the geometry of Figure 1 we have
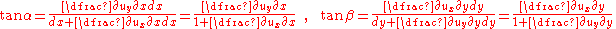
For small rotations, i.e. and
and 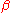 are
are  we have
we have

and, again, for small displacement gradients, we have
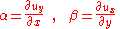
thus
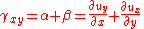
By interchanging and
and 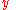 and
and 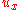 and
and 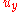 , it can be shown that
, it can be shown that 
Similarly, for the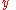 -
- and
and  -
- planes, we have
planes, we have

It can be seen that the tensorial shear strain components of the infinitesimal strain tensor can then be expressed using the engineering strain definition,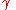 , as
, as
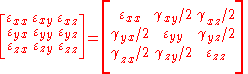
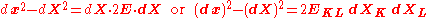
For infinitesimal strains then we have

Dividing by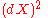 we have
we have
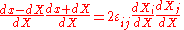
For small deformations we assume that , thus the second term of the left hand side becomes:
, thus the second term of the left hand side becomes: 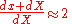 .
.
Then we have
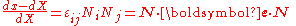
where , is the unit vector in the direction of
, is the unit vector in the direction of  , and the left-hand-side expression is the normal strain
, and the left-hand-side expression is the normal strain 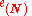 in the direction of
in the direction of  . For the particular case of
. For the particular case of  in the
in the 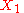 direction, i.e.
direction, i.e.  , we have
, we have
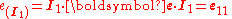
Similarly, for and
and  we can find the normal strains
we can find the normal strains  and
and 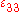 , respectively. Therefore, the diagonal elements of the infinitesimal strain tensor are the normal strains in the coordinate directions.
, respectively. Therefore, the diagonal elements of the infinitesimal strain tensor are the normal strains in the coordinate directions.
(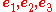 ) we can write the tensor in terms of components with respect to those base vectors as
) we can write the tensor in terms of components with respect to those base vectors as
In matrix form,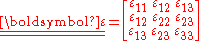
We can easily choose to use another orthonormal coordinate system (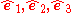 ) instead. In that case the components of the tensor are different, say
) instead. In that case the components of the tensor are different, say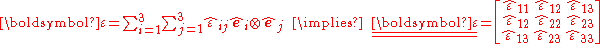
The components of the strain in the two coordinate systems are related by
where the Einstein summation convention for repeated indices has been used and . In matrix form
. In matrix form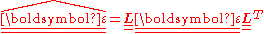
or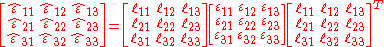
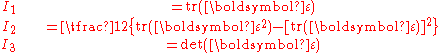
In terms of components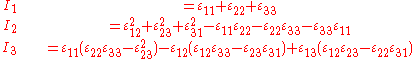
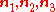 ) in which the components of the strain tensor are
) in which the components of the strain tensor are
The components of the strain tensor in the ( ) coordinate system are called the principal strains and the directions
) coordinate system are called the principal strains and the directions 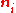 are called the directions of principal strain. Since there are no shear strain components in this coordinate system, the principal strains represent the maximum and minimum stretches of an elemental volume.
are called the directions of principal strain. Since there are no shear strain components in this coordinate system, the principal strains represent the maximum and minimum stretches of an elemental volume.
If we are given the components of the strain tensor in an arbitrary orthonormal coordinate system, we can find the principal strains using an eigenvalue decomposition determined by solving the system of equations
This system of equations is equivalent to finding the vector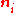 along which the strain tensor becomes a pure stretch with no shear component.
along which the strain tensor becomes a pure stretch with no shear component.
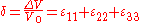
Actually, if we consider a cube with an edge length a, it is a quasi-cube after the deformation (the variations of the angles do not change the volume) with the dimensions and V0 = a3, thus
and V0 = a3, thus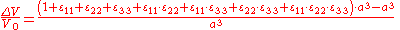
as we consider small deformations,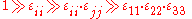
therefore the formula.
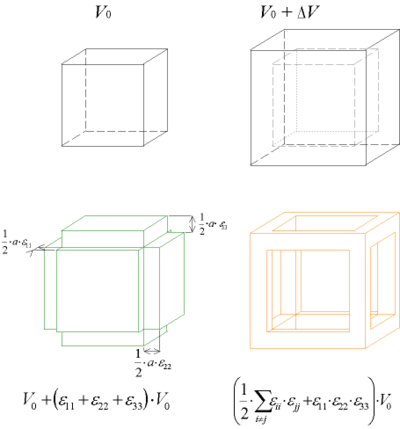
Real variation of volume (top) and the approximated one (bottom): the green drawing shows the estimated volume and the orange drawing the neglected volume
In case of pure shear, we can see that there is no change of the volume.
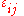 , similarly to the stress tensor, can be expressed as the sum of two other tensors:
, similarly to the stress tensor, can be expressed as the sum of two other tensors:

where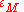 is the mean strain given by
is the mean strain given by
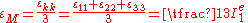
The deviatoric strain tensor can be obtained by subtracting the mean strain tensor from the infinitesimal strain tensor:
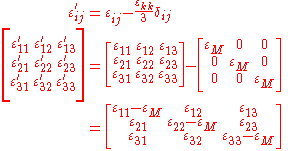
 ) be the directions of the three principal strains. An octahedral plane is whose normal makes equal angles with the three principal directions. The engineering shear strain on an octahedral plane is called the octahedral shear strain and is given by
) be the directions of the three principal strains. An octahedral plane is whose normal makes equal angles with the three principal directions. The engineering shear strain on an octahedral plane is called the octahedral shear strain and is given by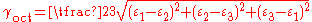
where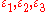 are the principal strains.
are the principal strains.
The normal strain on an octahedral plane is given by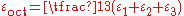
equivalent strain, is often used to describe the state of strain in solids. Several definitions of equivalent strain can be found in the literature. A definition that is commonly used in the literature on plasticity
is
This quantity is work conjugate to the equivalent stress defined as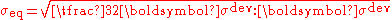
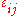 the strain tensor equation
the strain tensor equation 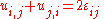 represents a system of six differential equations for the determination of three displacements components
represents a system of six differential equations for the determination of three displacements components 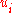 , giving an over-determined system. Thus, a solution does not generally exist for an arbitrary choice of strain components. Therefore, some restrictions, named compatibility equations, are imposed upon the strain components. With the addition of the three compatibility equations the number of independent equations is reduced to three, matching the number of unknown displacement components. These constraints on the strain tensor were discovered by Saint-Venant
, giving an over-determined system. Thus, a solution does not generally exist for an arbitrary choice of strain components. Therefore, some restrictions, named compatibility equations, are imposed upon the strain components. With the addition of the three compatibility equations the number of independent equations is reduced to three, matching the number of unknown displacement components. These constraints on the strain tensor were discovered by Saint-Venant
, and are called the "Saint Venant compatibility equations".
The compatibility functions serve to assure a single-valued continuous displacement function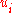 . If the elastic medium is visualised as a set of infinitesimal cubes in the unstrained state, after the medium is strained, an arbitrary strain tensor may not yield a situation in which the distorted cubes still fit together without overlapping.
. If the elastic medium is visualised as a set of infinitesimal cubes in the unstrained state, after the medium is strained, an arbitrary strain tensor may not yield a situation in which the distorted cubes still fit together without overlapping.
In index notation, the compatibility equations are expressed as
(and strain) are 3-D tensor
s but in prismatic structures such as a long metal billet, the length of the structure is much greater than the other two dimensions. The strains associated with length, i.e., the normal strain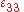 and the shear strains
and the shear strains 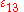 and
and 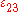 (if the length is the 3-direction) are constrained by nearby material and are small compared to the cross-sectional strains. The strain tensor can then be approximated by:
(if the length is the 3-direction) are constrained by nearby material and are small compared to the cross-sectional strains. The strain tensor can then be approximated by:
Continuum mechanics
Continuum mechanics is a branch of mechanics that deals with the analysis of the kinematics and the mechanical behavior of materials modelled as a continuous mass rather than as discrete particles...
, the infinitesimal
Infinitesimal
Infinitesimals have been used to express the idea of objects so small that there is no way to see them or to measure them. The word infinitesimal comes from a 17th century Modern Latin coinage infinitesimus, which originally referred to the "infinite-th" item in a series.In common speech, an...
strain theory, sometimes called small deformation theory, small displacement theory, or small displacement-gradient theory, deals with infinitesimal deformation
Deformation (mechanics)
Deformation in continuum mechanics is the transformation of a body from a reference configuration to a current configuration. A configuration is a set containing the positions of all particles of the body...
s of a continuum body
Continuum mechanics
Continuum mechanics is a branch of mechanics that deals with the analysis of the kinematics and the mechanical behavior of materials modelled as a continuous mass rather than as discrete particles...
. For an infinitesimal deformation the displacements
 and the displacement gradients
and the displacement gradients  are small compared to unity, i.e.,
are small compared to unity, i.e.,  and
and  , allowing for the geometric linearisation of the Lagrangian finite strain tensor
, allowing for the geometric linearisation of the Lagrangian finite strain tensor  , and the Eulerian finite strain tensor
, and the Eulerian finite strain tensor  , i.e. the non-linear or second-order terms of the finite strain tensor can be neglected. The linearised Lagrangian and Eulerian strain tensors are approximately the same and can be approximated by the infinitesimal strain tensor or Cauchy's strain tensor,
, i.e. the non-linear or second-order terms of the finite strain tensor can be neglected. The linearised Lagrangian and Eulerian strain tensors are approximately the same and can be approximated by the infinitesimal strain tensor or Cauchy's strain tensor, 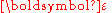 . Thus,
. Thus,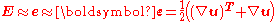
or

The infinitesimal strain theory is used in the analysis of deformations of materials exhibiting elastic
Elasticity (physics)
In physics, elasticity is the physical property of a material that returns to its original shape after the stress that made it deform or distort is removed. The relative amount of deformation is called the strain....
behaviour, such as materials found in mechanical and civil engineering applications, e.g. concrete and steel.
Infinitesimal strain tensor
For infinitesimal deformations of a continuum bodyContinuum mechanics
Continuum mechanics is a branch of mechanics that deals with the analysis of the kinematics and the mechanical behavior of materials modelled as a continuous mass rather than as discrete particles...
, in which the displacements and the displacement gradients are small compared to unity, i.e.,
 and
and  , it is possible to perform a geometric linearisation of the Lagrangian finite strain tensor
, it is possible to perform a geometric linearisation of the Lagrangian finite strain tensor  , and the Eulerian finite strain tensor
, and the Eulerian finite strain tensor  . In such a linearisation, the non-linear or second-order terms of the finite strain tensor are neglected. Thus we have
. In such a linearisation, the non-linear or second-order terms of the finite strain tensor are neglected. Thus we have
or
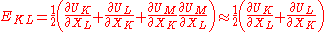
and
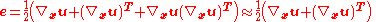
or
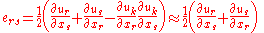
This linearisation implies that the Lagrangian description and the Eulerian description are approximately the same as there is little difference in the material and spatial coordinates of a given material point in the continuum. Therefore, the material displacement gradient components and the spatial displacement gradient components are approximately equal. Thus we have
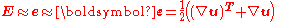
or

where
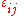 are the components of the infinitesimal strain tensor
are the components of the infinitesimal strain tensor 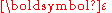 , also called Cauchy's strain tensor, linear strain tensor, or small strain tensor.
, also called Cauchy's strain tensor, linear strain tensor, or small strain tensor.
or using different notation:

Furthermore, since the deformation gradient can be expressed as
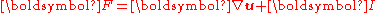 where
where  is the second-order identity tensor, we have
is the second-order identity tensor, we have
Also, from the general expression for the Lagrangian and Eulerian finite strain tensors we have

Geometric derivation of the infinitesimal strain tensor

 by
by 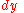 (Figure 1), which after deformation, takes the form of a rhombus. From the geometry of Figure 1 we have
(Figure 1), which after deformation, takes the form of a rhombus. From the geometry of Figure 1 we have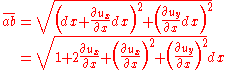
For very small displacement gradients, i.e.,
 , we have
, we have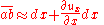
The normal strain in the
 -direction of the rectangular element is defined by
-direction of the rectangular element is defined by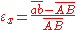
and knowing that
 , we have
, we have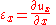
Similarly, the normal strain in the
 -direction, and
-direction, and  -direction, becomes
-direction, becomes
The engineering shear strain, or the change in angle between two originally orthogonal material lines, in this case line
 and
and  , is defined as
, is defined as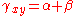
From the geometry of Figure 1 we have
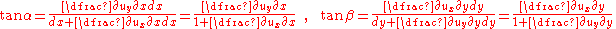
For small rotations, i.e.
 and
and 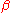 are
are  we have
we have
and, again, for small displacement gradients, we have
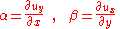
thus
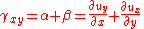
By interchanging
 and
and 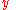 and
and 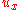 and
and 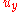 , it can be shown that
, it can be shown that 
Similarly, for the
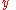 -
- and
and  -
- planes, we have
planes, we have
It can be seen that the tensorial shear strain components of the infinitesimal strain tensor can then be expressed using the engineering strain definition,
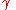 , as
, as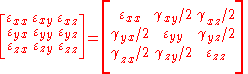
Physical interpretation of the infinitesimal strain tensor
From finite strain theory we have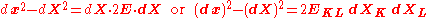
For infinitesimal strains then we have

Dividing by
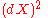 we have
we have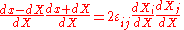
For small deformations we assume that
 , thus the second term of the left hand side becomes:
, thus the second term of the left hand side becomes: 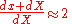 .
.Then we have
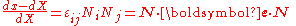
where
 , is the unit vector in the direction of
, is the unit vector in the direction of  , and the left-hand-side expression is the normal strain
, and the left-hand-side expression is the normal strain 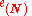 in the direction of
in the direction of  . For the particular case of
. For the particular case of  in the
in the 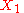 direction, i.e.
direction, i.e.  , we have
, we have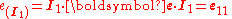
Similarly, for
 and
and  we can find the normal strains
we can find the normal strains  and
and 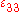 , respectively. Therefore, the diagonal elements of the infinitesimal strain tensor are the normal strains in the coordinate directions.
, respectively. Therefore, the diagonal elements of the infinitesimal strain tensor are the normal strains in the coordinate directions.Strain transformation rules
If we choose an orthonormal coordinate systemOrthonormal basis
In mathematics, particularly linear algebra, an orthonormal basis for inner product space V with finite dimension is a basis for V whose vectors are orthonormal. For example, the standard basis for a Euclidean space Rn is an orthonormal basis, where the relevant inner product is the dot product of...
(
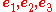 ) we can write the tensor in terms of components with respect to those base vectors as
) we can write the tensor in terms of components with respect to those base vectors as
In matrix form,
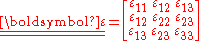
We can easily choose to use another orthonormal coordinate system (
 ) instead. In that case the components of the tensor are different, say
) instead. In that case the components of the tensor are different, say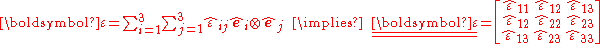
The components of the strain in the two coordinate systems are related by

where the Einstein summation convention for repeated indices has been used and
 . In matrix form
. In matrix form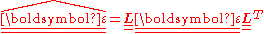
or
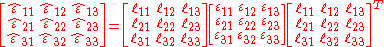
Strain invariants
Certain operations on the strain tensor give the same result without regard to which orthonormal coordinate system is used to represent the components of strain. The results of these operations are called strain invariants. The most commonly used strain invariants are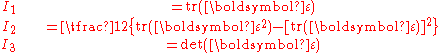
In terms of components
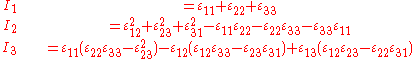
Principal strains
It can be shown that it is possible to find a coordinate system (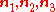 ) in which the components of the strain tensor are
) in which the components of the strain tensor are
The components of the strain tensor in the (
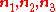 ) coordinate system are called the principal strains and the directions
) coordinate system are called the principal strains and the directions 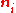 are called the directions of principal strain. Since there are no shear strain components in this coordinate system, the principal strains represent the maximum and minimum stretches of an elemental volume.
are called the directions of principal strain. Since there are no shear strain components in this coordinate system, the principal strains represent the maximum and minimum stretches of an elemental volume.If we are given the components of the strain tensor in an arbitrary orthonormal coordinate system, we can find the principal strains using an eigenvalue decomposition determined by solving the system of equations

This system of equations is equivalent to finding the vector
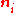 along which the strain tensor becomes a pure stretch with no shear component.
along which the strain tensor becomes a pure stretch with no shear component.Volumetric strain
The dilatation (the relative variation of the volume) is the trace of the tensor: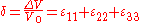
Actually, if we consider a cube with an edge length a, it is a quasi-cube after the deformation (the variations of the angles do not change the volume) with the dimensions
 and V0 = a3, thus
and V0 = a3, thus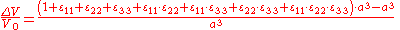
as we consider small deformations,
therefore the formula.

Real variation of volume (top) and the approximated one (bottom): the green drawing shows the estimated volume and the orange drawing the neglected volume
In case of pure shear, we can see that there is no change of the volume.
Strain deviator tensor
The infinitesimal strain tensor , similarly to the stress tensor, can be expressed as the sum of two other tensors:
, similarly to the stress tensor, can be expressed as the sum of two other tensors:
- a mean strain tensor or volumetric strain tensor or spherical strain tensor,
 , related to dilation or volume change; and
, related to dilation or volume change; and - a deviatoric component called the strain deviator tensor,
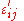 , related to distortion.
, related to distortion.

where
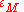 is the mean strain given by
is the mean strain given by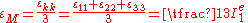
The deviatoric strain tensor can be obtained by subtracting the mean strain tensor from the infinitesimal strain tensor:
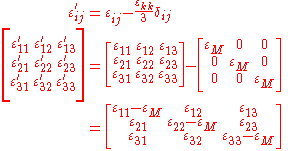
Octahedral strains
Let ( ) be the directions of the three principal strains. An octahedral plane is whose normal makes equal angles with the three principal directions. The engineering shear strain on an octahedral plane is called the octahedral shear strain and is given by
) be the directions of the three principal strains. An octahedral plane is whose normal makes equal angles with the three principal directions. The engineering shear strain on an octahedral plane is called the octahedral shear strain and is given by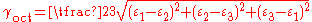
where
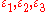 are the principal strains.
are the principal strains.The normal strain on an octahedral plane is given by
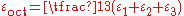
Equivalent strain
A scalar quantity called the equivalent strain, or the von MisesVon Mises
von Mises may refer to:* Ludwig von Mises Institute* von Mises distribution, named after Richard von Mises* von Mises yield criterion, named after Richard von Mises- People :* Dr...
equivalent strain, is often used to describe the state of strain in solids. Several definitions of equivalent strain can be found in the literature. A definition that is commonly used in the literature on plasticity
Plasticity
Plasticity may refer to:Science* Plasticity , in physics and engineering, plasticity is the propensity of a material to undergo permanent deformation under load...
is

This quantity is work conjugate to the equivalent stress defined as
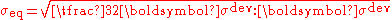
Compatibility equations
For prescribed strain components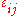 the strain tensor equation
the strain tensor equation 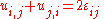 represents a system of six differential equations for the determination of three displacements components
represents a system of six differential equations for the determination of three displacements components 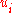 , giving an over-determined system. Thus, a solution does not generally exist for an arbitrary choice of strain components. Therefore, some restrictions, named compatibility equations, are imposed upon the strain components. With the addition of the three compatibility equations the number of independent equations is reduced to three, matching the number of unknown displacement components. These constraints on the strain tensor were discovered by Saint-Venant
, giving an over-determined system. Thus, a solution does not generally exist for an arbitrary choice of strain components. Therefore, some restrictions, named compatibility equations, are imposed upon the strain components. With the addition of the three compatibility equations the number of independent equations is reduced to three, matching the number of unknown displacement components. These constraints on the strain tensor were discovered by Saint-VenantAdhémar Jean Claude Barré de Saint-Venant
Adhémar Jean Claude Barré de Saint-Venant was a mechanician and mathematician who contributed to early stress analysis and also developed the one-dimensional unsteady open channel flow shallow water equations or Saint-Venant equations that are a fundamental set of equations used in modern...
, and are called the "Saint Venant compatibility equations".
The compatibility functions serve to assure a single-valued continuous displacement function
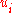 . If the elastic medium is visualised as a set of infinitesimal cubes in the unstrained state, after the medium is strained, an arbitrary strain tensor may not yield a situation in which the distorted cubes still fit together without overlapping.
. If the elastic medium is visualised as a set of infinitesimal cubes in the unstrained state, after the medium is strained, an arbitrary strain tensor may not yield a situation in which the distorted cubes still fit together without overlapping.In index notation, the compatibility equations are expressed as

| Engineering notation |
|---|
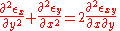 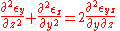 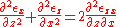 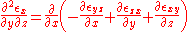 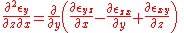 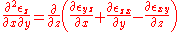 |
Plane strain
In real engineering components, stressStress (physics)
In continuum mechanics, stress is a measure of the internal forces acting within a deformable body. Quantitatively, it is a measure of the average force per unit area of a surface within the body on which internal forces act. These internal forces are a reaction to external forces applied on the body...
(and strain) are 3-D tensor
Tensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
s but in prismatic structures such as a long metal billet, the length of the structure is much greater than the other two dimensions. The strains associated with length, i.e., the normal strain
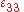 and the shear strains
and the shear strains 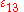 and
and 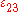 (if the length is the 3-direction) are constrained by nearby material and are small compared to the cross-sectional strains. The strain tensor can then be approximated by:
(if the length is the 3-direction) are constrained by nearby material and are small compared to the cross-sectional strains. The strain tensor can then be approximated by:-

in which the double underline indicates a second order tensorTensorTensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
. This strain state is called plane strain. The corresponding stress tensor is:
-
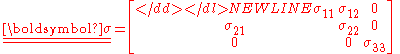
in which the non-zero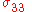 is needed to maintain the constraint
is needed to maintain the constraint  . This stress term can be temporarily removed from the analysis to leave only the in-plane terms, effectively reducing the 3-D problem to a much simpler 2-D problem.
. This stress term can be temporarily removed from the analysis to leave only the in-plane terms, effectively reducing the 3-D problem to a much simpler 2-D problem.
Antiplane strain
Antiplane strain is another special state of strain that can occur in a body, for instance in a region close to a screw dislocation. The strain tensor for antiplane strain is given by-
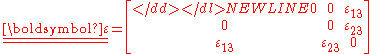
Infinitesimal rotation tensor
The infinitesimal strain tensor is defined as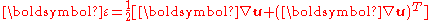
Therefore the displacement gradient can be expressed as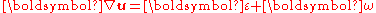
where
The quantity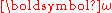 is the infinitesimal rotation tensor. This tensor is skew symmetric. For infinitesimal deformations the scalar components of
is the infinitesimal rotation tensor. This tensor is skew symmetric. For infinitesimal deformations the scalar components of 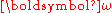 satisfy the condition
satisfy the condition 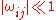 . Note that the displacement gradient is small only if both the strain tensor and the rotation tensor are infinitesimal.
. Note that the displacement gradient is small only if both the strain tensor and the rotation tensor are infinitesimal.
The axial vector
A skew symmetric second-order tensor has three independent scalar components. These three components are used to define an axial vector, , as follows
, as follows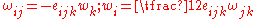
where is the permutation symbol. In matrix form
is the permutation symbol. In matrix form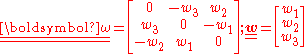
The axial vector is also called the infinitesimal rotation vector. The rotation vector is related to the displacement gradient by the relation
In index notation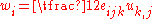
If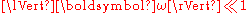 and
and  then the material undergoes an approximate rigid body rotation of magnitude
then the material undergoes an approximate rigid body rotation of magnitude  around the vector
around the vector  .
.
Relation between the strain tensor and the rotation vector
Given a continuous, single-valued displacement field and the corresponding infinitesimal strain tensor
and the corresponding infinitesimal strain tensor 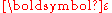 , we have (see Tensor derivative (continuum mechanics)Tensor derivative (continuum mechanics)The derivatives of scalars, vectors, and second-order tensors with respect to second-order tensors are of considerable use in continuum mechanics. These derivatives are used in the theories of nonlinear elasticity and plasticity, particularly in the design of algorithms for numerical...
, we have (see Tensor derivative (continuum mechanics)Tensor derivative (continuum mechanics)The derivatives of scalars, vectors, and second-order tensors with respect to second-order tensors are of considerable use in continuum mechanics. These derivatives are used in the theories of nonlinear elasticity and plasticity, particularly in the design of algorithms for numerical...
)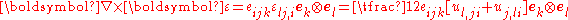
Since a change in the order of differentiation does not change the result,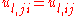 . Therefore
. Therefore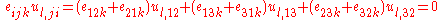
Also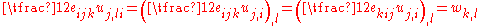
Hence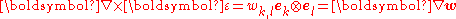
Relation between rotation tensor and rotation vector
From an important identity regarding the curl of a tensorTensor derivative (continuum mechanics)The derivatives of scalars, vectors, and second-order tensors with respect to second-order tensors are of considerable use in continuum mechanics. These derivatives are used in the theories of nonlinear elasticity and plasticity, particularly in the design of algorithms for numerical...
we know that for a continuous, single-valued displacement field ,
,
Since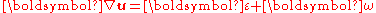 we have
we have

Strain tensor in cylindrical coordinates
In cylindrical polar coordinates ( ), the displacement vector can be written as
), the displacement vector can be written as
The components of the strain tensor in a cylindrical coordinate system are given by
Strain tensor in spherical coordinates
In spherical coordinates (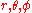 ), the displacement vector can be written as
), the displacement vector can be written as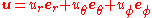
The components of the strain tensor in a spherical coordinate system are given by
See also
- Deformation (mechanics)Deformation (mechanics)Deformation in continuum mechanics is the transformation of a body from a reference configuration to a current configuration. A configuration is a set containing the positions of all particles of the body...
- Compatibility (mechanics)Compatibility (mechanics)In continuum mechanics, a compatible deformation tensor field in a body is that unique field that is obtained when the body is subjected to a continuous, single-valued, displacement field. Compatibility is the study of the conditions under which such a displacement field can be guaranteed...
- StressStress (physics)In continuum mechanics, stress is a measure of the internal forces acting within a deformable body. Quantitatively, it is a measure of the average force per unit area of a surface within the body on which internal forces act. These internal forces are a reaction to external forces applied on the body...
- Strain gaugeStrain gaugeA strain gauge is a device used to measure the strain of an object. Invented by Edward E. Simmons and Arthur C. Ruge in 1938, the most common type of strain gauge consists of an insulating flexible backing which supports a metallic foil pattern. The gauge is attached to the object by a suitable...
- Stress–strain curve
- Hooke's lawHooke's lawIn mechanics, and physics, Hooke's law of elasticity is an approximation that states that the extension of a spring is in direct proportion with the load applied to it. Many materials obey this law as long as the load does not exceed the material's elastic limit. Materials for which Hooke's law...
- Poisson's ratioPoisson's ratioPoisson's ratio , named after Siméon Poisson, is the ratio, when a sample object is stretched, of the contraction or transverse strain , to the extension or axial strain ....
- Finite strain theory
- Strain rate
- Plane stress
- Digital image correlationDigital image correlationDigital Image Correlation and Tracking is an optical method that employs tracking & image registration techniques for accurate 2D and 3D measurements of changes in images. This is often used to measure deformation , displacement, and strain, but it is widely applied in many areas of science and...
External links
- Deformation (mechanics)
-
-

