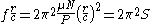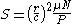Sommerfeld number
Encyclopedia
In the design of fluid bearings
, the Sommerfeld number, or bearing characteristic number, is a dimensionless quantity
used extensively in hydrodynamic lubrication analysis. The Sommerfeld number is very important in lubrication analysis because it contains all the variables normally specified by the designer.
The Sommerfeld number is named after Arnold Sommerfeld
(1868 –1951).
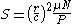
Where:
shaft and bearing, was the first to explain the phenomenon of bearing
friction
. This method, which ultimately produces the equation known as Petroff's Law, is useful because it defines groups of relevant dimensionless parameters, and predicts a fairly accurate coefficient of friction, even when the shaft is not concentric.
Considering a vertical shaft rotating inside a bearing, it can be assumed that the bearing is subjected to a negligible load, the radial clearance space is completely filled with lubricant, and that leakage is negligible. The surface velocity of the shaft is: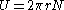
, where N is the rotational speed of the shaft in rev/s.
The shear stress
in the lubricant can be represented as follows:
Assuming a constant rate of shear,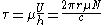
The torque
required to shear the film is
If a small radial load W acts on the shaft and hence the bearing, the frictional drag force can be considered equal to the product fW, with the friction torque represented as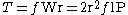
Where
If the small radial load W is considered negligible, setting the two expressions for torque equal to one another and solving for the coefficient of friction yields
Which is known as Petroff's Law or the Petroff equation.
It provides a quick and simple means of obtaining reasonable estimates of coefficients of friction of lightly loaded bearings.
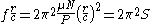
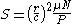
Fluid bearing
Fluid bearings are bearings which support the bearing's loads solely on a thin layer of liquid or gas.They can be broadly classified as fluid dynamic bearings or hydrostatic bearings. Hydrostatic bearings are externally pressurized fluid bearings, where the fluid is usually oil, water or air, and...
, the Sommerfeld number, or bearing characteristic number, is a dimensionless quantity
Dimensionless quantity
In dimensional analysis, a dimensionless quantity or quantity of dimension one is a quantity without an associated physical dimension. It is thus a "pure" number, and as such always has a dimension of 1. Dimensionless quantities are widely used in mathematics, physics, engineering, economics, and...
used extensively in hydrodynamic lubrication analysis. The Sommerfeld number is very important in lubrication analysis because it contains all the variables normally specified by the designer.
The Sommerfeld number is named after Arnold Sommerfeld
Arnold Sommerfeld
Arnold Johannes Wilhelm Sommerfeld was a German theoretical physicist who pioneered developments in atomic and quantum physics, and also educated and groomed a large number of students for the new era of theoretical physics...
(1868 –1951).
Definition
The Sommerfeld Number is typically defined by the following equation.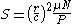Where:
- S is the Sommerfeld Number or bearing characteristic number
- r is the shaft radius
- c is the radial clearance
- μ is the absolute viscosity of the lubricant
- N is the speed of the rotating shaft in revs/s
- P is the load per unit of projected bearing area
Petroff's Law
Petroff's method of lubrication analysis, which assumes a concentricConcentric
Concentric objects share the same center, axis or origin with one inside the other. Circles, tubes, cylindrical shafts, disks, and spheres may be concentric to one another...
shaft and bearing, was the first to explain the phenomenon of bearing
Bearing (mechanical)
A bearing is a device to allow constrained relative motion between two or more parts, typically rotation or linear movement. Bearings may be classified broadly according to the motions they allow and according to their principle of operation as well as by the directions of applied loads they can...
friction
Friction
Friction is the force resisting the relative motion of solid surfaces, fluid layers, and/or material elements sliding against each other. There are several types of friction:...
. This method, which ultimately produces the equation known as Petroff's Law, is useful because it defines groups of relevant dimensionless parameters, and predicts a fairly accurate coefficient of friction, even when the shaft is not concentric.
Considering a vertical shaft rotating inside a bearing, it can be assumed that the bearing is subjected to a negligible load, the radial clearance space is completely filled with lubricant, and that leakage is negligible. The surface velocity of the shaft is:
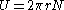, where N is the rotational speed of the shaft in rev/s.The shear stress
Shear stress
A shear stress, denoted \tau\, , is defined as the component of stress coplanar with a material cross section. Shear stress arises from the force vector component parallel to the cross section...
in the lubricant can be represented as follows:
Assuming a constant rate of shear,
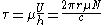
The torque
Torque
Torque, moment or moment of force , is the tendency of a force to rotate an object about an axis, fulcrum, or pivot. Just as a force is a push or a pull, a torque can be thought of as a twist....
required to shear the film is
If a small radial load W acts on the shaft and hence the bearing, the frictional drag force can be considered equal to the product fW, with the friction torque represented as
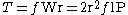
Where
- W is the force acting on the bearing
- P is the radial load per unit of project bearing area (Pressure)
-
is the coefficient of friction
If the small radial load W is considered negligible, setting the two expressions for torque equal to one another and solving for the coefficient of friction yields
Which is known as Petroff's Law or the Petroff equation.
It provides a quick and simple means of obtaining reasonable estimates of coefficients of friction of lightly loaded bearings.
Sommerfeld number
Multiplying both sides of Petroff's Law by the clearance ratio r/c,