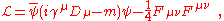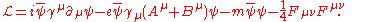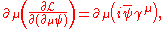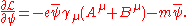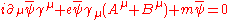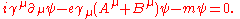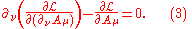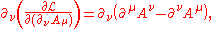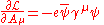Quantum electrodynamics
Encyclopedia
Quantum electrodynamics (QED) is the relativistic quantum field theory
of electrodynamics. In essence, it describes how light
and matter
interact and is the first theory where full agreement between quantum mechanics
and special relativity
is achieved. QED mathematically describes all phenomena
involving electrically charged
particles interacting by means of exchange of photon
s and represents the quantum
counterpart of classical electrodynamics giving a complete account of matter and light interaction. One of the founding fathers of QED, Richard Feynman
, has called it "the jewel of physics" for its extremely accurate predictions
of quantities like the anomalous magnetic moment of the electron, and the Lamb shift of the energy level
s of hydrogen
.
In technical terms, QED can be described as a perturbation theory
of the electromagnetic
quantum vacuum
.
describing radiation and matter interaction is due to British scientist Paul Adrien Maurice Dirac, who, during 1920, was first able to compute the coefficient of spontaneous emission of an atom
.
Dirac described the quantization of the electromagnetic field
as an ensemble of harmonic oscillator
s with the introduction of the concept of creation and annihilation operators
of particles. In the following years, with contributions from Wolfgang Pauli
, Eugene Wigner, Pascual Jordan
, Werner Heisenberg
and an elegant formulation of quantum electrodynamics due to Enrico Fermi
, physicists came to believe that, in principle, it would be possible to perform any computation for any physical process involving photons and charged particles. However, further studies by Felix Bloch
with Arnold Nordsieck, and Victor Weisskopf, in 1937 and 1939, revealed that such computations were reliable only at a first order of perturbation theory
, a problem already pointed out by Robert Oppenheimer
. At higher orders in the series infinities emerged, making such computations meaningless and casting serious doubts on the internal consistency of the theory itself. With no solution for this problem known at the time, it appeared that a fundamental incompatibility existed between special relativity
and quantum mechanics
.
 Difficulties with the theory increased through the end of 1940. Improvements in microwave
Difficulties with the theory increased through the end of 1940. Improvements in microwave
technology made it possible to take more precise measurements of the shift of the levels of a hydrogen atom
, now known as the Lamb shift and magnetic moment
of the electron. These experiments unequivocally exposed discrepancies which the theory was unable to explain.
A first indication of a possible way out was given by Hans Bethe
. In 1947, while he was traveling by train to reach Schenectady from New York
, after giving a talk at the conference at Shelter Island
on the subject, Bethe completed the first non-relativistic computation of the shift of the lines of the hydrogen atom as measured by Lamb and Retherford. Despite the limitations of the computation, agreement was excellent. The idea was simply to attach infinities to corrections at mass
and charge
that were actually fixed to a finite value by experiments. In this way, the infinities get absorbed in those constants and yield a finite result in good agreement with experiments. This procedure was named renormalization
.
 Based on Bethe's intuition and fundamental papers on the subject by Sin-Itiro Tomonaga
Based on Bethe's intuition and fundamental papers on the subject by Sin-Itiro Tomonaga
, Julian Schwinger
, Richard Feynman
and Freeman Dyson
, it was finally possible to get fully covariant
formulations that were finite at any order in a perturbation series of quantum electrodynamics. Sin-Itiro Tomonaga
, Julian Schwinger
and Richard Feynman
were jointly awarded with a Nobel prize in physics
in 1965 for their work in this area. Their contributions, and those of Freeman Dyson
, were about covariant
and gauge invariant formulations of quantum electrodynamics that allow computations of observables at any order of perturbation theory
. Feynman's mathematical technique, based on his diagrams
, initially seemed very different from the field-theoretic, operator
-based approach of Schwinger and Tomonaga, but Freeman Dyson
later showed that the two approaches were equivalent. Renormalization
, the need to attach a physical meaning at certain divergences appearing in the theory through integral
s, has subsequently become one of the fundamental aspects of quantum field theory
and has come to be seen as a criterion for a theory's general acceptability. Even though renormalization works very well in practice, Feynman was never entirely comfortable with its mathematical validity, even referring to renormalization as a "shell game" and "hocus pocus
".
QED has served as the model and template for all subsequent quantum field theories. One such subsequent theory is quantum chromodynamics
, which began in the early 1960s and attained its present form in the 1975 work by H. David Politzer, Sidney Coleman
, David Gross
and Frank Wilczek
. Building on the pioneering work of Schwinger, Gerald Guralnik
, Dick Hagen
, and Tom Kibble
, Peter Higgs
, Jeffrey Goldstone
, and others, Sheldon Glashow, Steven Weinberg
and Abdus Salam
independently showed how the weak nuclear force and quantum electrodynamics could be merged into a single electroweak force.
, a classic non-mathematical exposition of QED from the point of view articulated below.
The key components of Feynman's presentation of QED are three basic actions.
These actions are represented in a form of visual shorthand by the three basic elements of Feynman diagrams: a wavy line for the photon, a straight line for the electron and a junction of two straight lines and a wavy one for a vertex representing emission or absorption of a photon by an electron. These may all be seen in the adjacent diagram.
It is important not to over-interpret these diagrams. Nothing is implied about how a particle gets from one point to another. The diagrams do not imply that the particles are moving in straight or curved lines. They do not imply that the particles are moving with fixed speeds. The fact that the photon is often represented, by convention, by a wavy line and not a straight one does not imply that it is thought that it is more wavelike than is an electron. The images are just symbols to represent the actions above: photons and electrons do, somehow, move from point to point and electrons, somehow, emit and absorb photons. We do not know how these things happen, but the theory tells us about the probabilities of these things happening.
As well as the visual shorthand for the actions Feynman introduces another kind of shorthand for the numerical quantities which tell us about the probabilities. If a photon moves from one place and time – in shorthand, A – to another place and time – shorthand, B – the associated quantity is written in Feynman's shorthand as P(A to B). The similar quantity for an electron moving from C to D is written E(C to D). The quantity which tells us about the probability for the emission or absorption of a photon he calls 'j'. This is related to, but not the same as, the measured electron charge
'e'.
QED is based on the assumption that complex interactions of many electrons and photons can be represented by fitting together a suitable collection of the above three building blocks, and then using the probability-quantities to calculate the probability of any such complex interaction. It turns out that the basic idea of QED can be communicated while making the assumption that the quantities mentioned above are just our everyday probabilities
. (A simplification of Feynman's book.) Later on this will be corrected to include specifically quantum mathematics, following Feynman.
The basic rules of probabilities that will be used are that a) if an event can happen in a variety of different ways then its probability is the sum of the probabilities of the possible ways and b) if a process involves a number of independent subprocesses then its probability is the product of the component probabilities.
.) But there is another possibility: that is that the electron first moves to G where it emits a photon which goes on to D, while the electron moves on to H, where it absorbs the first photon, before moving on to C. Again we can calculate the probability of these possibilities (for all points G and H). We then have a better estimation for the total probability by adding the probabilities of these two possibilities to our original simple estimate. Incidentally the name given to this process of a photon interacting with an electron in this way is Compton Scattering
.
There are an infinite number of other intermediate processes in which more and more photons are absorbed and/or emitted. For each of these possibilities there is a Feynman diagram describing it. This implies a complex computation for the resulting probabilities, but provided it is the case that the more complicated the diagram the less it contributes to the result, it is only a matter of time and effort to find as accurate an answer as one wants to the original question. This is the basic approach of QED. To calculate the probability of any interactive process between electrons and photons it is a matter of first noting, with Feynman diagrams, all the possible ways in which the process can be constructed from the three basic elements. Each diagram involves some calculation involving definite rules to find the associated probability.
That basic scaffolding remains when one moves to a quantum description but some conceptual changes are needed. One is that whereas we might expect in our everyday life that there would be some constraints on the points to which a particle can move, that is not true in full quantum electrodynamics. There is a possibility of an electron at A, or a photon at B, moving as a basic action to any other place and time in the universe. That includes places that could only be reached at speeds greater than that of light and also earlier times. (An electron moving backwards in time can be viewed as a positron
moving forward in time.)
introduces an important change on the way probabilities are computed. It has been found that the quantities which we have to use to represent the probabilities are not the usual real numbers we use for probabilities in our everyday world, but complex number
s which are called probability amplitude
s. Feynman avoids exposing the reader to the mathematics of complex numbers by using a simple but accurate representation of them as arrows on a piece of paper or screen. (These must not be confused with the arrows of Feynman diagrams which are actually simplified representations in two dimensions of a relationship between points in three dimensions of space and one of time.) The amplitude-arrows are fundamental to the description of the world given by quantum theory. No satisfactory reason has been given for why they are needed. But pragmatically we have to accept that they are an essential part of our description of all quantum phenomena. They are related to our everyday ideas of probability by the simple rule that the probability of an event is the square of the length of the corresponding amplitude-arrow. So, for a given process, if two probability amplitudes, v and w, are involved, the probability of the process will be given either by

or
 .
.
The rules as regards adding or multiplying, however, are the same as above. But where you would expect to add or multiply probabilities, instead you add or multiply probability amplitudes that now are complex numbers.
Addition and multiplication are familiar operations in the theory of complex numbers and are given in the figures. The sum is found as follows. Let the start of the second arrow be at the end of the first. The sum is then a third arrow that goes directly from the start of the first to the end of the second. The product of two arrows is an arrow whose length is the product of the two lengths. The direction of the product is found by adding the angles that each of the two have been turned through relative to a reference direction: that gives the angle that the product is turned relative to the reference direction.
That change, from probabilities to probability amplitudes, complicates the mathematics without changing the basic approach. But that change is still not quite enough because it fails to take into account the fact that both photons and electrons can be polarized, which is to say that their orientation in space and time have to be taken into account. Therefore P(A to B) actually consists of 16 complex numbers, or probability amplitude arrows. There are also some minor changes to do with the quantity "j", which may have to be rotated by a multiple of 90º for some polarizations, which is only of interest for the detailed bookkeeping.
Associated with the fact that the electron can be polarized is another small necessary detail which is connected with the fact that an electron is a Fermion
and obeys Fermi-Dirac statistics
. The basic rule is that if we have the probability amplitude for a given complex process involving more than one electron, then when we include (as we always must) the complementary Feynman diagram in which we just exchange two electron events, the resulting amplitude is the reverse – the negative – of the first. The simplest case would be two electrons starting at A and B ending at C and D. The amplitude would be calculated as the "difference", E(A to B)xE(C to D) – E(A to C)xE(B to D), where we would expect, from our everyday idea of probabilities, that it would be a sum.
which describes the behavior of the electron's probability amplitude and the Klein-Gordon equation
which describes the behavior of the photon's probability amplitude. These are called Feynman propagators
. The translation to a notation commonly used in the standard literature is as follows:
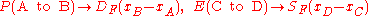
where a shorthand symbol such as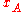 stands for the four real numbers which give the time and position in three dimensions of the point labeled A.
stands for the four real numbers which give the time and position in three dimensions of the point labeled A.
in which if we look closely at a line it breaks up into a collection of "simple" lines, each of which, if looked at closely, are in turn composed of "simple" lines, and so on ad infinitum. This is a very difficult situation to handle. If adding that detail only altered things slightly then it would not have been too bad, but disaster struck when it was found that the simple correction mentioned above led to infinite probability amplitudes. In time this problem was "fixed" by the technique of renormalization
(see below and the article on mass renormalization
). However, Feynman himself remained unhappy about it, calling it a "dippy process".
. However, as Feynman points out, it fails totally to explain why particles such as the electron have the masses they do. "There is no theory that adequately explains these numbers. We use the numbers in all our theories, but we don't understand them – what they are, or where they come from. I believe that from a fundamental point of view, this is a very interesting and serious problem."
gauge theory
with the symmetry group U(1). The gauge field, which mediates the interaction between the charged spin-1/2
field
s, is the electromagnetic field
.
The QED Lagrangian
for a spin-1/2 field interacting with the electromagnetic field is given by the real part of
Next, we can substitute this Lagrangian into the Euler-Lagrange equation
of motion for a field:
to find the field equations for QED.
The two terms from this Lagrangian are then
Substituting these two back into the Euler-Lagrange equation (2) results in
with complex conjugate
Bringing the middle term to the right-hand side transforms this second equation into
|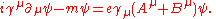
|}
The left-hand side is like the original Dirac equation
and the right-hand side is the interaction with the electromagnetic field.
One further important equation can be found by substituting the Lagrangian into another Euler-Lagrange equation, this time for the field,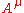 :
:
The two terms this time are
and these two terms, when substituted back into (3) give us
|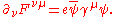
|}
Now, if we impose the Lorenz-Gauge condition, i.e., that the divergence of the four potential vanishes then we get
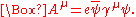
that, for a given initial state, will give a final state in such a way to have
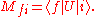
This technique is also known as the S-Matrix. Evolution operator is obtained in the interaction picture
where time evolution is given by the interaction Hamiltonian. So, from equations above is
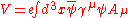
and so, one has

being T the time ordering
operator. This evolution operator has only a meaning as a series and what we get here is a perturbation series
with a development parameter being fine structure constant
. This series is named Dyson series
.
s of the propagator
s. Quantum physics considers particle's momenta
rather than their positions, and it is convenient to think of particles as being created or annihilated when they interact. Feynman diagrams then look the same, but the lines have different interpretations. The electron line represents an electron with a given energy and momentum, with a similar interpretation of the photon line. A vertex diagram represents the annihilation of one electron and the creation of another together with the absorption or creation of a photon, each having specified energies and momenta.
Using Wick theorem on the terms of the Dyson series, all the terms of the S-matrix for quantum electrodynamics can be computed through the technique of Feynman diagrams. In this case rules for drawing are the following
To these rules we must add a further one for closed loops that implies an integration on momenta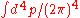 .
.
From them, computations of probability amplitude
s are straightforwardly given. An example is Compton scattering
, with an electron
and a photon
undergoing elastic scattering
. Feynman diagrams are in this case
and so we are able to get the corresponding amplitude at the first order of a perturbation series
for S-matrix:

from which we are able to compute the cross section
for this scattering.
that, being closed loops, imply the presence of diverging integral
s having no mathematical meaning. To overcome this difficulty, a technique like renormalization
has been devised, producing finite results in very close agreement with experiments. It is important to note that a criterion for theory being meaningful after renormalization is that the number of diverging diagrams is finite. In this case the theory is said renormalizable. The reason for this is that to get observables renormalized one needs a finite number of constants to maintain the predictive value of the theory untouched. This is exactly the case of quantum electrodynamics displaying just three diverging diagrams. This procedure gives observables in very close agreement with experiment as seen e.g. for electron gyromagnetic ratio.
Renormalizability has become an essential criterion for a quantum field theory
to be considered as a viable one. All the theories describing fundamental interaction
s, except gravitation
whose quantum counterpart is presently under very active research, are renormalizable theories.
shows that the radius of convergence
of the perturbation series in QED is zero. The basic argument goes as follows: if the coupling constant were negative, this would be equivalent to the Coulomb force constant being negative. This would "reverse" the electromagnetic interaction so that like charges would attract and unlike charges would repel. This would render the vacuum unstable against decay into a cluster of electrons on one side of the universe and a cluster of positrons on the other side of the universe. Because the theory is 'sick' for any negative value of the coupling constant, the series do not converge, but are an asymptotic series. This can be taken as a need for a new theory, a problem with perturbation theory
, or ignored by taking a "shut-up-and-calculate" approach.
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
of electrodynamics. In essence, it describes how light
Light
Light or visible light is electromagnetic radiation that is visible to the human eye, and is responsible for the sense of sight. Visible light has wavelength in a range from about 380 nanometres to about 740 nm, with a frequency range of about 405 THz to 790 THz...
and matter
Matter
Matter is a general term for the substance of which all physical objects consist. Typically, matter includes atoms and other particles which have mass. A common way of defining matter is as anything that has mass and occupies volume...
interact and is the first theory where full agreement between quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
and special relativity
Special relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
is achieved. QED mathematically describes all phenomena
Phenomenon
A phenomenon , plural phenomena, is any observable occurrence. Phenomena are often, but not always, understood as 'appearances' or 'experiences'...
involving electrically charged
Electric charge
Electric charge is a physical property of matter that causes it to experience a force when near other electrically charged matter. Electric charge comes in two types, called positive and negative. Two positively charged substances, or objects, experience a mutual repulsive force, as do two...
particles interacting by means of exchange of photon
Photon
In physics, a photon is an elementary particle, the quantum of the electromagnetic interaction and the basic unit of light and all other forms of electromagnetic radiation. It is also the force carrier for the electromagnetic force...
s and represents the quantum
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
counterpart of classical electrodynamics giving a complete account of matter and light interaction. One of the founding fathers of QED, Richard Feynman
Richard Feynman
Richard Phillips Feynman was an American physicist known for his work in the path integral formulation of quantum mechanics, the theory of quantum electrodynamics and the physics of the superfluidity of supercooled liquid helium, as well as in particle physics...
, has called it "the jewel of physics" for its extremely accurate predictions
Precision tests of QED
Quantum electrodynamics , a relativistic quantum field theory of electrodynamics, is among the most stringently tested theories in physics....
of quantities like the anomalous magnetic moment of the electron, and the Lamb shift of the energy level
Energy level
A quantum mechanical system or particle that is bound -- that is, confined spatially—can only take on certain discrete values of energy. This contrasts with classical particles, which can have any energy. These discrete values are called energy levels...
s of hydrogen
Hydrogen
Hydrogen is the chemical element with atomic number 1. It is represented by the symbol H. With an average atomic weight of , hydrogen is the lightest and most abundant chemical element, constituting roughly 75% of the Universe's chemical elemental mass. Stars in the main sequence are mainly...
.
In technical terms, QED can be described as a perturbation theory
Perturbation theory (quantum mechanics)
In quantum mechanics, perturbation theory is a set of approximation schemes directly related to mathematical perturbation for describing a complicated quantum system in terms of a simpler one. The idea is to start with a simple system for which a mathematical solution is known, and add an...
of the electromagnetic
Electromagnetism
Electromagnetism is one of the four fundamental interactions in nature. The other three are the strong interaction, the weak interaction and gravitation...
quantum vacuum
Vacuum state
In quantum field theory, the vacuum state is the quantum state with the lowest possible energy. Generally, it contains no physical particles...
.
History
The first formulation of a quantum theoryQuantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
describing radiation and matter interaction is due to British scientist Paul Adrien Maurice Dirac, who, during 1920, was first able to compute the coefficient of spontaneous emission of an atom
Atom
The atom is a basic unit of matter that consists of a dense central nucleus surrounded by a cloud of negatively charged electrons. The atomic nucleus contains a mix of positively charged protons and electrically neutral neutrons...
.
Dirac described the quantization of the electromagnetic field
Electromagnetic field
An electromagnetic field is a physical field produced by moving electrically charged objects. It affects the behavior of charged objects in the vicinity of the field. The electromagnetic field extends indefinitely throughout space and describes the electromagnetic interaction...
as an ensemble of harmonic oscillator
Harmonic oscillator
In classical mechanics, a harmonic oscillator is a system that, when displaced from its equilibrium position, experiences a restoring force, F, proportional to the displacement, x: \vec F = -k \vec x \, where k is a positive constant....
s with the introduction of the concept of creation and annihilation operators
Creation and annihilation operators
Creation and annihilation operators are mathematical operators that have widespread applications in quantum mechanics, notably in the study of quantum harmonic oscillators and many-particle systems. An annihilation operator lowers the number of particles in a given state by one...
of particles. In the following years, with contributions from Wolfgang Pauli
Wolfgang Pauli
Wolfgang Ernst Pauli was an Austrian theoretical physicist and one of the pioneers of quantum physics. In 1945, after being nominated by Albert Einstein, he received the Nobel Prize in Physics for his "decisive contribution through his discovery of a new law of Nature, the exclusion principle or...
, Eugene Wigner, Pascual Jordan
Pascual Jordan
-Further reading:...
, Werner Heisenberg
Werner Heisenberg
Werner Karl Heisenberg was a German theoretical physicist who made foundational contributions to quantum mechanics and is best known for asserting the uncertainty principle of quantum theory...
and an elegant formulation of quantum electrodynamics due to Enrico Fermi
Enrico Fermi
Enrico Fermi was an Italian-born, naturalized American physicist particularly known for his work on the development of the first nuclear reactor, Chicago Pile-1, and for his contributions to the development of quantum theory, nuclear and particle physics, and statistical mechanics...
, physicists came to believe that, in principle, it would be possible to perform any computation for any physical process involving photons and charged particles. However, further studies by Felix Bloch
Felix Bloch
Felix Bloch was a Swiss physicist, working mainly in the U.S.-Life and work:Bloch was born in Zürich, Switzerland to Jewish parents Gustav and Agnes Bloch. He was educated there and at the Eidgenössische Technische Hochschule, also in Zürich. Initially studying engineering he soon changed to physics...
with Arnold Nordsieck, and Victor Weisskopf, in 1937 and 1939, revealed that such computations were reliable only at a first order of perturbation theory
Perturbation theory (quantum mechanics)
In quantum mechanics, perturbation theory is a set of approximation schemes directly related to mathematical perturbation for describing a complicated quantum system in terms of a simpler one. The idea is to start with a simple system for which a mathematical solution is known, and add an...
, a problem already pointed out by Robert Oppenheimer
Robert Oppenheimer
Julius Robert Oppenheimer was an American theoretical physicist and professor of physics at the University of California, Berkeley. Along with Enrico Fermi, he is often called the "father of the atomic bomb" for his role in the Manhattan Project, the World War II project that developed the first...
. At higher orders in the series infinities emerged, making such computations meaningless and casting serious doubts on the internal consistency of the theory itself. With no solution for this problem known at the time, it appeared that a fundamental incompatibility existed between special relativity
Special relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
and quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
.

Microwave
Microwaves, a subset of radio waves, have wavelengths ranging from as long as one meter to as short as one millimeter, or equivalently, with frequencies between 300 MHz and 300 GHz. This broad definition includes both UHF and EHF , and various sources use different boundaries...
technology made it possible to take more precise measurements of the shift of the levels of a hydrogen atom
Hydrogen atom
A hydrogen atom is an atom of the chemical element hydrogen. The electrically neutral atom contains a single positively-charged proton and a single negatively-charged electron bound to the nucleus by the Coulomb force...
, now known as the Lamb shift and magnetic moment
Magnetic moment
The magnetic moment of a magnet is a quantity that determines the force that the magnet can exert on electric currents and the torque that a magnetic field will exert on it...
of the electron. These experiments unequivocally exposed discrepancies which the theory was unable to explain.
A first indication of a possible way out was given by Hans Bethe
Hans Bethe
Hans Albrecht Bethe was a German-American nuclear physicist, and Nobel laureate in physics for his work on the theory of stellar nucleosynthesis. A versatile theoretical physicist, Bethe also made important contributions to quantum electrodynamics, nuclear physics, solid-state physics and...
. In 1947, while he was traveling by train to reach Schenectady from New York
New York
New York is a state in the Northeastern region of the United States. It is the nation's third most populous state. New York is bordered by New Jersey and Pennsylvania to the south, and by Connecticut, Massachusetts and Vermont to the east...
, after giving a talk at the conference at Shelter Island
Shelter Island Conference
The first Shelter Island Conference on the Foundations of Quantum Mechanics was held from June 2–4, 1947 at the Ram's Head Inn in Shelter Island, New York. Shelter Island was the first major opportunity since Pearl Harbor and the Manhattan Project for the leaders of the American physics community...
on the subject, Bethe completed the first non-relativistic computation of the shift of the lines of the hydrogen atom as measured by Lamb and Retherford. Despite the limitations of the computation, agreement was excellent. The idea was simply to attach infinities to corrections at mass
Mass
Mass can be defined as a quantitive measure of the resistance an object has to change in its velocity.In physics, mass commonly refers to any of the following three properties of matter, which have been shown experimentally to be equivalent:...
and charge
Charge
Charge or charged may refer to:* Charge , illegal contact by pushing or moving into another player's torso* Charge , a six-note trumpet or bugle piece denoting the call to rush forward...
that were actually fixed to a finite value by experiments. In this way, the infinities get absorbed in those constants and yield a finite result in good agreement with experiments. This procedure was named renormalization
Renormalization
In quantum field theory, the statistical mechanics of fields, and the theory of self-similar geometric structures, renormalization is any of a collection of techniques used to treat infinities arising in calculated quantities....
.

Sin-Itiro Tomonaga
was a Japanese physicist, influential in the development of quantum electrodynamics, work for which he was jointly awarded the Nobel Prize in Physics in 1965 along with Richard Feynman and Julian Schwinger.-Biography:...
, Julian Schwinger
Julian Schwinger
Julian Seymour Schwinger was an American theoretical physicist. He is best known for his work on the theory of quantum electrodynamics, in particular for developing a relativistically invariant perturbation theory, and for renormalizing QED to one loop order.Schwinger is recognized as one of the...
, Richard Feynman
Richard Feynman
Richard Phillips Feynman was an American physicist known for his work in the path integral formulation of quantum mechanics, the theory of quantum electrodynamics and the physics of the superfluidity of supercooled liquid helium, as well as in particle physics...
and Freeman Dyson
Freeman Dyson
Freeman John Dyson FRS is a British-born American theoretical physicist and mathematician, famous for his work in quantum field theory, solid-state physics, astronomy and nuclear engineering. Dyson is a member of the Board of Sponsors of the Bulletin of the Atomic Scientists...
, it was finally possible to get fully covariant
Lorentz covariance
In standard physics, Lorentz symmetry is "the feature of nature that says experimental results are independent of the orientation or the boost velocity of the laboratory through space"...
formulations that were finite at any order in a perturbation series of quantum electrodynamics. Sin-Itiro Tomonaga
Sin-Itiro Tomonaga
was a Japanese physicist, influential in the development of quantum electrodynamics, work for which he was jointly awarded the Nobel Prize in Physics in 1965 along with Richard Feynman and Julian Schwinger.-Biography:...
, Julian Schwinger
Julian Schwinger
Julian Seymour Schwinger was an American theoretical physicist. He is best known for his work on the theory of quantum electrodynamics, in particular for developing a relativistically invariant perturbation theory, and for renormalizing QED to one loop order.Schwinger is recognized as one of the...
and Richard Feynman
Richard Feynman
Richard Phillips Feynman was an American physicist known for his work in the path integral formulation of quantum mechanics, the theory of quantum electrodynamics and the physics of the superfluidity of supercooled liquid helium, as well as in particle physics...
were jointly awarded with a Nobel prize in physics
Nobel Prize in Physics
The Nobel Prize in Physics is awarded once a year by the Royal Swedish Academy of Sciences. It is one of the five Nobel Prizes established by the will of Alfred Nobel in 1895 and awarded since 1901; the others are the Nobel Prize in Chemistry, Nobel Prize in Literature, Nobel Peace Prize, and...
in 1965 for their work in this area. Their contributions, and those of Freeman Dyson
Freeman Dyson
Freeman John Dyson FRS is a British-born American theoretical physicist and mathematician, famous for his work in quantum field theory, solid-state physics, astronomy and nuclear engineering. Dyson is a member of the Board of Sponsors of the Bulletin of the Atomic Scientists...
, were about covariant
Lorentz covariance
In standard physics, Lorentz symmetry is "the feature of nature that says experimental results are independent of the orientation or the boost velocity of the laboratory through space"...
and gauge invariant formulations of quantum electrodynamics that allow computations of observables at any order of perturbation theory
Perturbation theory (quantum mechanics)
In quantum mechanics, perturbation theory is a set of approximation schemes directly related to mathematical perturbation for describing a complicated quantum system in terms of a simpler one. The idea is to start with a simple system for which a mathematical solution is known, and add an...
. Feynman's mathematical technique, based on his diagrams
Feynman diagram
Feynman diagrams are a pictorial representation scheme for the mathematical expressions governing the behavior of subatomic particles, first developed by the Nobel Prize-winning American physicist Richard Feynman, and first introduced in 1948...
, initially seemed very different from the field-theoretic, operator
Operator (physics)
In physics, an operator is a function acting on the space of physical states. As a resultof its application on a physical state, another physical state is obtained, very often along withsome extra relevant information....
-based approach of Schwinger and Tomonaga, but Freeman Dyson
Freeman Dyson
Freeman John Dyson FRS is a British-born American theoretical physicist and mathematician, famous for his work in quantum field theory, solid-state physics, astronomy and nuclear engineering. Dyson is a member of the Board of Sponsors of the Bulletin of the Atomic Scientists...
later showed that the two approaches were equivalent. Renormalization
Renormalization
In quantum field theory, the statistical mechanics of fields, and the theory of self-similar geometric structures, renormalization is any of a collection of techniques used to treat infinities arising in calculated quantities....
, the need to attach a physical meaning at certain divergences appearing in the theory through integral
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
s, has subsequently become one of the fundamental aspects of quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
and has come to be seen as a criterion for a theory's general acceptability. Even though renormalization works very well in practice, Feynman was never entirely comfortable with its mathematical validity, even referring to renormalization as a "shell game" and "hocus pocus
Hocus Pocus
Hocus pocus, hocus-pocus, or hokus pokus is a term used by magicians, usually the magic words spoken when bringing about some sort of change.It may also refer to:-Books:* Hocus Pocus , a 1990 novel by Kurt Vonnegut...
".
QED has served as the model and template for all subsequent quantum field theories. One such subsequent theory is quantum chromodynamics
Quantum chromodynamics
In theoretical physics, quantum chromodynamics is a theory of the strong interaction , a fundamental force describing the interactions of the quarks and gluons making up hadrons . It is the study of the SU Yang–Mills theory of color-charged fermions...
, which began in the early 1960s and attained its present form in the 1975 work by H. David Politzer, Sidney Coleman
Sidney Coleman
Sidney Richard Coleman was an American theoretical physicist who studied under Murray Gell-Mann.- Life and work :Sidney Coleman grew up on the Far North Side of Chicago...
, David Gross
David Gross
David Jonathan Gross is an American particle physicist and string theorist. Along with Frank Wilczek and David Politzer, he was awarded the 2004 Nobel Prize in Physics for their discovery of asymptotic freedom. He is currently the director and holder of the Frederick W...
and Frank Wilczek
Frank Wilczek
Frank Anthony Wilczek is a theoretical physicist from the United States and a Nobel laureate. He is currently the Herman Feshbach Professor of Physics at the Massachusetts Institute of Technology ....
. Building on the pioneering work of Schwinger, Gerald Guralnik
Gerald Guralnik
Gerald Stanford Guralnik is the Chancellor’s Professor of Physics at Brown University. He is most famous for his co-discovery of the Higgs mechanism and Higgs Boson with C. R. Hagen and Tom Kibble...
, Dick Hagen
C. R. Hagen
Carl Richard Hagen is a professor of particle physics at the University of Rochester. He is most noted for his contributions to the Standard Model and Symmetry breaking as well as the co-discovery of the Higgs mechanism and Higgs boson with Gerald Guralnik and Tom Kibble...
, and Tom Kibble
Tom W. B. Kibble
Thomas Walter Bannerman Kibble, FRS, is a British scientist and senior research investigator at The Blackett Laboratory, at Imperial College London, UK. His research interests are in quantum field theory, especially the interface between high-energy particle physics and cosmology...
, Peter Higgs
Peter Higgs
Peter Ware Higgs, FRS, FRSE, FKC , is an English theoretical physicist and an emeritus professor at the University of Edinburgh....
, Jeffrey Goldstone
Jeffrey Goldstone
Jeffrey Goldstone is a British-born theoretical physicist and an emeritus physics faculty at MIT Center for Theoretical Physics.He worked at the University of Cambridge until 1977....
, and others, Sheldon Glashow, Steven Weinberg
Steven Weinberg
Steven Weinberg is an American theoretical physicist and Nobel laureate in Physics for his contributions with Abdus Salam and Sheldon Glashow to the unification of the weak force and electromagnetic interaction between elementary particles....
and Abdus Salam
Abdus Salam
Mohammad Abdus Salam, NI, SPk Mohammad Abdus Salam, NI, SPk Mohammad Abdus Salam, NI, SPk (Urdu: محمد عبد السلام, pronounced , (January 29, 1926– November 21, 1996) was a Pakistani theoretical physicist and Nobel laureate in Physics for his work on the electroweak unification of the...
independently showed how the weak nuclear force and quantum electrodynamics could be merged into a single electroweak force.
Introduction
Near the end of his life, Richard P. Feynman gave a series of lectures on QED intended for the lay public. These lectures were transcribed and published as Feynman (1985), QED: The strange theory of light and matterQED (book)
QED: The Strange Theory of Light and Matter is an adaptation for the general reader of four lectures on quantum electrodynamics by Richard Feynman ....
, a classic non-mathematical exposition of QED from the point of view articulated below.
The key components of Feynman's presentation of QED are three basic actions.
- A photonPhotonIn physics, a photon is an elementary particle, the quantum of the electromagnetic interaction and the basic unit of light and all other forms of electromagnetic radiation. It is also the force carrier for the electromagnetic force...
goes from one place and time to another place and time. - An electronElectronThe electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
goes from one place and time to another place and time. - An electron emits or absorbs a photon at a certain place and time.
These actions are represented in a form of visual shorthand by the three basic elements of Feynman diagrams: a wavy line for the photon, a straight line for the electron and a junction of two straight lines and a wavy one for a vertex representing emission or absorption of a photon by an electron. These may all be seen in the adjacent diagram.
It is important not to over-interpret these diagrams. Nothing is implied about how a particle gets from one point to another. The diagrams do not imply that the particles are moving in straight or curved lines. They do not imply that the particles are moving with fixed speeds. The fact that the photon is often represented, by convention, by a wavy line and not a straight one does not imply that it is thought that it is more wavelike than is an electron. The images are just symbols to represent the actions above: photons and electrons do, somehow, move from point to point and electrons, somehow, emit and absorb photons. We do not know how these things happen, but the theory tells us about the probabilities of these things happening.
As well as the visual shorthand for the actions Feynman introduces another kind of shorthand for the numerical quantities which tell us about the probabilities. If a photon moves from one place and time – in shorthand, A – to another place and time – shorthand, B – the associated quantity is written in Feynman's shorthand as P(A to B). The similar quantity for an electron moving from C to D is written E(C to D). The quantity which tells us about the probability for the emission or absorption of a photon he calls 'j'. This is related to, but not the same as, the measured electron charge
Elementary charge
The elementary charge, usually denoted as e, is the electric charge carried by a single proton, or equivalently, the absolute value of the electric charge carried by a single electron. This elementary charge is a fundamental physical constant. To avoid confusion over its sign, e is sometimes called...
'e'.
QED is based on the assumption that complex interactions of many electrons and photons can be represented by fitting together a suitable collection of the above three building blocks, and then using the probability-quantities to calculate the probability of any such complex interaction. It turns out that the basic idea of QED can be communicated while making the assumption that the quantities mentioned above are just our everyday probabilities
Probability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
. (A simplification of Feynman's book.) Later on this will be corrected to include specifically quantum mathematics, following Feynman.
The basic rules of probabilities that will be used are that a) if an event can happen in a variety of different ways then its probability is the sum of the probabilities of the possible ways and b) if a process involves a number of independent subprocesses then its probability is the product of the component probabilities.
Basic constructions
Suppose we start with one electron at a certain place and time (this place and time being given the arbitrary label A) and a photon at another place and time (given the label B). A typical question from a physical standpoint is: 'What is the probability of finding an electron at C (another place and a later time) and a photon at D (yet another place and time)?'. The simplest process to achieve this end is for the electron to move from A to C (an elementary action) and that the photon moves from B to D (another elementary action). From a knowledge of the probabilities of each of these subprocesses – E(A to C) and P(B to D) – then we would expect to calculate the probability of both happening by multiplying them, using rule b) above. This gives a simple estimated answer to our question. But there are other ways in which the end result could come about. The electron might move to a place and time E where it absorbs the photon; then move on before emitting another photon at F; then move on to C where it is detected, while the new photon moves on to D. The probability of this complex process can again be calculated by knowing the probabilities of each of the individual actions: three electron actions, two photon actions and two vertexes – one emission and one absorption. We would expect to find the total probability by multiplying the probabilities of each of the actions, for any chosen positions of E and F. We then, using rule a) above, have to add up all these probabilities for all the alternatives for E and F. (This is not elementary in practice, and involves integrationIntegral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
.) But there is another possibility: that is that the electron first moves to G where it emits a photon which goes on to D, while the electron moves on to H, where it absorbs the first photon, before moving on to C. Again we can calculate the probability of these possibilities (for all points G and H). We then have a better estimation for the total probability by adding the probabilities of these two possibilities to our original simple estimate. Incidentally the name given to this process of a photon interacting with an electron in this way is Compton Scattering
Compton scattering
In physics, Compton scattering is a type of scattering that X-rays and gamma rays undergo in matter. The inelastic scattering of photons in matter results in a decrease in energy of an X-ray or gamma ray photon, called the Compton effect...
.
There are an infinite number of other intermediate processes in which more and more photons are absorbed and/or emitted. For each of these possibilities there is a Feynman diagram describing it. This implies a complex computation for the resulting probabilities, but provided it is the case that the more complicated the diagram the less it contributes to the result, it is only a matter of time and effort to find as accurate an answer as one wants to the original question. This is the basic approach of QED. To calculate the probability of any interactive process between electrons and photons it is a matter of first noting, with Feynman diagrams, all the possible ways in which the process can be constructed from the three basic elements. Each diagram involves some calculation involving definite rules to find the associated probability.
That basic scaffolding remains when one moves to a quantum description but some conceptual changes are needed. One is that whereas we might expect in our everyday life that there would be some constraints on the points to which a particle can move, that is not true in full quantum electrodynamics. There is a possibility of an electron at A, or a photon at B, moving as a basic action to any other place and time in the universe. That includes places that could only be reached at speeds greater than that of light and also earlier times. (An electron moving backwards in time can be viewed as a positron
Positron
The positron or antielectron is the antiparticle or the antimatter counterpart of the electron. The positron has an electric charge of +1e, a spin of ½, and has the same mass as an electron...
moving forward in time.)
Probability amplitudes
Quantum mechanicsQuantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
introduces an important change on the way probabilities are computed. It has been found that the quantities which we have to use to represent the probabilities are not the usual real numbers we use for probabilities in our everyday world, but complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s which are called probability amplitude
Probability amplitude
In quantum mechanics, a probability amplitude is a complex number whose modulus squared represents a probability or probability density.For example, if the probability amplitude of a quantum state is \alpha, the probability of measuring that state is |\alpha|^2...
s. Feynman avoids exposing the reader to the mathematics of complex numbers by using a simple but accurate representation of them as arrows on a piece of paper or screen. (These must not be confused with the arrows of Feynman diagrams which are actually simplified representations in two dimensions of a relationship between points in three dimensions of space and one of time.) The amplitude-arrows are fundamental to the description of the world given by quantum theory. No satisfactory reason has been given for why they are needed. But pragmatically we have to accept that they are an essential part of our description of all quantum phenomena. They are related to our everyday ideas of probability by the simple rule that the probability of an event is the square of the length of the corresponding amplitude-arrow. So, for a given process, if two probability amplitudes, v and w, are involved, the probability of the process will be given either by

or
 .
.The rules as regards adding or multiplying, however, are the same as above. But where you would expect to add or multiply probabilities, instead you add or multiply probability amplitudes that now are complex numbers.
Addition and multiplication are familiar operations in the theory of complex numbers and are given in the figures. The sum is found as follows. Let the start of the second arrow be at the end of the first. The sum is then a third arrow that goes directly from the start of the first to the end of the second. The product of two arrows is an arrow whose length is the product of the two lengths. The direction of the product is found by adding the angles that each of the two have been turned through relative to a reference direction: that gives the angle that the product is turned relative to the reference direction.
That change, from probabilities to probability amplitudes, complicates the mathematics without changing the basic approach. But that change is still not quite enough because it fails to take into account the fact that both photons and electrons can be polarized, which is to say that their orientation in space and time have to be taken into account. Therefore P(A to B) actually consists of 16 complex numbers, or probability amplitude arrows. There are also some minor changes to do with the quantity "j", which may have to be rotated by a multiple of 90º for some polarizations, which is only of interest for the detailed bookkeeping.
Associated with the fact that the electron can be polarized is another small necessary detail which is connected with the fact that an electron is a Fermion
Fermion
In particle physics, a fermion is any particle which obeys the Fermi–Dirac statistics . Fermions contrast with bosons which obey Bose–Einstein statistics....
and obeys Fermi-Dirac statistics
Fermi-Dirac statistics
Fermi–Dirac statistics is a part of the science of physics that describes the energies of single particles in a system comprising many identical particles that obey the Pauli Exclusion Principle...
. The basic rule is that if we have the probability amplitude for a given complex process involving more than one electron, then when we include (as we always must) the complementary Feynman diagram in which we just exchange two electron events, the resulting amplitude is the reverse – the negative – of the first. The simplest case would be two electrons starting at A and B ending at C and D. The amplitude would be calculated as the "difference", E(A to B)xE(C to D) – E(A to C)xE(B to D), where we would expect, from our everyday idea of probabilities, that it would be a sum.
Propagators
Finally, one has to compute P(A to B) and E (C to D) corresponding to the probability amplitudes for the photon and the electron respectively. These are essentially the solutions of the Dirac EquationDirac equation
The Dirac equation is a relativistic quantum mechanical wave equation formulated by British physicist Paul Dirac in 1928. It provided a description of elementary spin-½ particles, such as electrons, consistent with both the principles of quantum mechanics and the theory of special relativity, and...
which describes the behavior of the electron's probability amplitude and the Klein-Gordon equation
Klein-Gordon equation
The Klein–Gordon equation is a relativistic version of the Schrödinger equation....
which describes the behavior of the photon's probability amplitude. These are called Feynman propagators
Propagator
In quantum mechanics and quantum field theory, the propagator gives the probability amplitude for a particle to travel from one place to another in a given time, or to travel with a certain energy and momentum. Propagators are used to represent the contribution of virtual particles on the internal...
. The translation to a notation commonly used in the standard literature is as follows:
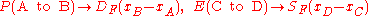
where a shorthand symbol such as
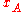 stands for the four real numbers which give the time and position in three dimensions of the point labeled A.
stands for the four real numbers which give the time and position in three dimensions of the point labeled A.Mass renormalization
A problem arose historically which held up progress for twenty years: although we start with the assumption of three basic "simple" actions, the rules of the game say that if we want to calculate the probability amplitude for an electron to get from A to B we must take into account all the possible ways: all possible Feynman diagrams with those end points. Thus there will be a way in which the electron travels to C, emits a photon there and then absorbs it again at D before moving on to B. Or it could do this kind of thing twice, or more. In short we have a fractal-like situationFractal
A fractal has been defined as "a rough or fragmented geometric shape that can be split into parts, each of which is a reduced-size copy of the whole," a property called self-similarity...
in which if we look closely at a line it breaks up into a collection of "simple" lines, each of which, if looked at closely, are in turn composed of "simple" lines, and so on ad infinitum. This is a very difficult situation to handle. If adding that detail only altered things slightly then it would not have been too bad, but disaster struck when it was found that the simple correction mentioned above led to infinite probability amplitudes. In time this problem was "fixed" by the technique of renormalization
Renormalization
In quantum field theory, the statistical mechanics of fields, and the theory of self-similar geometric structures, renormalization is any of a collection of techniques used to treat infinities arising in calculated quantities....
(see below and the article on mass renormalization
Self-energy
In theoretical physics and quantum field theory a particle's self-energy \Sigma represents the contribution to the particle's energy, or effective mass, due to interactions between the particle and the system it is part of...
). However, Feynman himself remained unhappy about it, calling it a "dippy process".
Conclusions
Within the above framework physicists were then able to calculate to a high degree of accuracy some of the properties of electrons, such as the anomalous magnetic dipole momentAnomalous magnetic dipole moment
In quantum electrodynamics, the anomalous magnetic moment of a particle is a contribution of effects of quantum mechanics, expressed by Feynman diagrams with loops, to the magnetic moment of that particle...
. However, as Feynman points out, it fails totally to explain why particles such as the electron have the masses they do. "There is no theory that adequately explains these numbers. We use the numbers in all our theories, but we don't understand them – what they are, or where they come from. I believe that from a fundamental point of view, this is a very interesting and serious problem."
Mathematics
Mathematically, QED is an abelianAbelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
gauge theory
Gauge theory
In physics, gauge invariance is the property of a field theory in which different configurations of the underlying fundamental but unobservable fields result in identical observable quantities. A theory with such a property is called a gauge theory...
with the symmetry group U(1). The gauge field, which mediates the interaction between the charged spin-1/2
Spin (physics)
In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,...
field
Field (physics)
In physics, a field is a physical quantity associated with each point of spacetime. A field can be classified as a scalar field, a vector field, a spinor field, or a tensor field according to whether the value of the field at each point is a scalar, a vector, a spinor or, more generally, a tensor,...
s, is the electromagnetic field
Electromagnetic field
An electromagnetic field is a physical field produced by moving electrically charged objects. It affects the behavior of charged objects in the vicinity of the field. The electromagnetic field extends indefinitely throughout space and describes the electromagnetic interaction...
.
The QED Lagrangian
Lagrangian
The Lagrangian, L, of a dynamical system is a function that summarizes the dynamics of the system. It is named after Joseph Louis Lagrange. The concept of a Lagrangian was originally introduced in a reformulation of classical mechanics by Irish mathematician William Rowan Hamilton known as...
for a spin-1/2 field interacting with the electromagnetic field is given by the real part of
- where
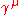 are Dirac matrices;
are Dirac matrices; a bispinorBispinorIn physics, bispinor is a four-component object which transforms under the ⊕ representation of the covariance group of special relativity...
a bispinorBispinorIn physics, bispinor is a four-component object which transforms under the ⊕ representation of the covariance group of special relativity...
fieldField (physics)In physics, a field is a physical quantity associated with each point of spacetime. A field can be classified as a scalar field, a vector field, a spinor field, or a tensor field according to whether the value of the field at each point is a scalar, a vector, a spinor or, more generally, a tensor,...
of spin-1/2 particles (e.g. electronElectronThe electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
-positronPositronThe positron or antielectron is the antiparticle or the antimatter counterpart of the electron. The positron has an electric charge of +1e, a spin of ½, and has the same mass as an electron...
field);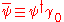 , called "psi-bar", is sometimes referred to as Dirac adjoint;
, called "psi-bar", is sometimes referred to as Dirac adjoint; is the gauge covariant derivativeGauge covariant derivativeThe gauge covariant derivative is like a generalization of the covariant derivative used in general relativity. If a theory has gauge transformations, it means that some physical properties of certain equations are preserved under those transformations...
is the gauge covariant derivativeGauge covariant derivativeThe gauge covariant derivative is like a generalization of the covariant derivative used in general relativity. If a theory has gauge transformations, it means that some physical properties of certain equations are preserved under those transformations...
; is the coupling constantFine-structure constantIn physics, the fine-structure constant is a fundamental physical constant, namely the coupling constant characterizing the strength of the electromagnetic interaction. Being a dimensionless quantity, it has constant numerical value in all systems of units...
is the coupling constantFine-structure constantIn physics, the fine-structure constant is a fundamental physical constant, namely the coupling constant characterizing the strength of the electromagnetic interaction. Being a dimensionless quantity, it has constant numerical value in all systems of units...
, equal to the electric chargeElectric chargeElectric charge is a physical property of matter that causes it to experience a force when near other electrically charged matter. Electric charge comes in two types, called positive and negative. Two positively charged substances, or objects, experience a mutual repulsive force, as do two...
of the bispinor field;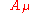 is the covariant four-potential of the electromagnetic field generated by the electron itself;
is the covariant four-potential of the electromagnetic field generated by the electron itself; is the external field imposed by external source;
is the external field imposed by external source;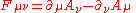 is the electromagnetic field tensor.
is the electromagnetic field tensor.
Equations of motion
To begin, substituting the definition of D into the Lagrangian gives usNext, we can substitute this Lagrangian into the Euler-Lagrange equation
Euler-Lagrange equation
In calculus of variations, the Euler–Lagrange equation, Euler's equation, or Lagrange's equation, is a differential equation whose solutions are the functions for which a given functional is stationary...
of motion for a field:
to find the field equations for QED.
The two terms from this Lagrangian are then
Substituting these two back into the Euler-Lagrange equation (2) results in
with complex conjugate
Bringing the middle term to the right-hand side transforms this second equation into
-
- {|cellpadding="2" style="border:2px solid #ccccff"
|
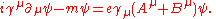
|}
The left-hand side is like the original Dirac equation
Dirac equation
The Dirac equation is a relativistic quantum mechanical wave equation formulated by British physicist Paul Dirac in 1928. It provided a description of elementary spin-½ particles, such as electrons, consistent with both the principles of quantum mechanics and the theory of special relativity, and...
and the right-hand side is the interaction with the electromagnetic field.
One further important equation can be found by substituting the Lagrangian into another Euler-Lagrange equation, this time for the field,
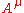 :
:
The two terms this time are
and these two terms, when substituted back into (3) give us
-
- {|cellpadding="2" style="border:2px solid #ccccff"
|
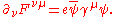
|}
Now, if we impose the Lorenz-Gauge condition, i.e., that the divergence of the four potential vanishes then we get
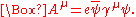
Interaction picture
This theory can be straightforwardly quantized treating bosonic and fermionic sectors as free. This permits to build a set of asymptotic states to start a computation of the probability amplitudes for different processes. In order to be able to do so, we have to compute an evolution operatorHamiltonian (quantum mechanics)
In quantum mechanics, the Hamiltonian H, also Ȟ or Ĥ, is the operator corresponding to the total energy of the system. Its spectrum is the set of possible outcomes when one measures the total energy of a system...
that, for a given initial state, will give a final state in such a way to have
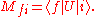
This technique is also known as the S-Matrix. Evolution operator is obtained in the interaction picture
Interaction picture
In quantum mechanics, the Interaction picture is an intermediate between the Schrödinger picture and the Heisenberg picture. Whereas in the other two pictures either the state vector or the operators carry time dependence, in the interaction picture both carry part of the time dependence of...
where time evolution is given by the interaction Hamiltonian. So, from equations above is
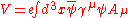
and so, one has

being T the time ordering
Path-ordering
In theoretical physics, path-ordering is the procedure of ordering a product of many operators according to the value of one chosen parameter:...
operator. This evolution operator has only a meaning as a series and what we get here is a perturbation series
Perturbation theory (quantum mechanics)
In quantum mechanics, perturbation theory is a set of approximation schemes directly related to mathematical perturbation for describing a complicated quantum system in terms of a simpler one. The idea is to start with a simple system for which a mathematical solution is known, and add an...
with a development parameter being fine structure constant
Fine-structure constant
In physics, the fine-structure constant is a fundamental physical constant, namely the coupling constant characterizing the strength of the electromagnetic interaction. Being a dimensionless quantity, it has constant numerical value in all systems of units...
. This series is named Dyson series
Dyson series
In scattering theory, the Dyson series, formulated by British-born American physicist Freeman Dyson, is a perturbative series, and each term is represented by Feynman diagrams. This series diverges asymptotically, but in quantum electrodynamics at the second order the difference from...
.
Feynman diagrams
Despite the conceptual clarity of this Feynman approach to QED, almost no textbooks follow him in their presentation. When performing calculations it is much easier to work with the Fourier transformFourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
s of the propagator
Propagator
In quantum mechanics and quantum field theory, the propagator gives the probability amplitude for a particle to travel from one place to another in a given time, or to travel with a certain energy and momentum. Propagators are used to represent the contribution of virtual particles on the internal...
s. Quantum physics considers particle's momenta
Momentum
In classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...
rather than their positions, and it is convenient to think of particles as being created or annihilated when they interact. Feynman diagrams then look the same, but the lines have different interpretations. The electron line represents an electron with a given energy and momentum, with a similar interpretation of the photon line. A vertex diagram represents the annihilation of one electron and the creation of another together with the absorption or creation of a photon, each having specified energies and momenta.
Using Wick theorem on the terms of the Dyson series, all the terms of the S-matrix for quantum electrodynamics can be computed through the technique of Feynman diagrams. In this case rules for drawing are the following
To these rules we must add a further one for closed loops that implies an integration on momenta
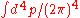 .
.From them, computations of probability amplitude
Probability amplitude
In quantum mechanics, a probability amplitude is a complex number whose modulus squared represents a probability or probability density.For example, if the probability amplitude of a quantum state is \alpha, the probability of measuring that state is |\alpha|^2...
s are straightforwardly given. An example is Compton scattering
Compton scattering
In physics, Compton scattering is a type of scattering that X-rays and gamma rays undergo in matter. The inelastic scattering of photons in matter results in a decrease in energy of an X-ray or gamma ray photon, called the Compton effect...
, with an electron
Electron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
and a photon
Photon
In physics, a photon is an elementary particle, the quantum of the electromagnetic interaction and the basic unit of light and all other forms of electromagnetic radiation. It is also the force carrier for the electromagnetic force...
undergoing elastic scattering
Elastic scattering
In scattering theory and in particular in particle physics, elastic scattering is one of the specific forms of scattering. In this process, the kinetic energy of the incident particles is conserved, only their direction of propagation is modified .-Electron elastic scattering:When an alpha particle...
. Feynman diagrams are in this case
and so we are able to get the corresponding amplitude at the first order of a perturbation series
Perturbation theory (quantum mechanics)
In quantum mechanics, perturbation theory is a set of approximation schemes directly related to mathematical perturbation for describing a complicated quantum system in terms of a simpler one. The idea is to start with a simple system for which a mathematical solution is known, and add an...
for S-matrix:

from which we are able to compute the cross section
Cross section (physics)
A cross section is the effective area which governs the probability of some scattering or absorption event. Together with particle density and path length, it can be used to predict the total scattering probability via the Beer-Lambert law....
for this scattering.
Renormalizability
Higher order terms can be straightforwardly computed for the evolution operator but these terms display diagrams containing the following simpler onesthat, being closed loops, imply the presence of diverging integral
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
s having no mathematical meaning. To overcome this difficulty, a technique like renormalization
Renormalization
In quantum field theory, the statistical mechanics of fields, and the theory of self-similar geometric structures, renormalization is any of a collection of techniques used to treat infinities arising in calculated quantities....
has been devised, producing finite results in very close agreement with experiments. It is important to note that a criterion for theory being meaningful after renormalization is that the number of diverging diagrams is finite. In this case the theory is said renormalizable. The reason for this is that to get observables renormalized one needs a finite number of constants to maintain the predictive value of the theory untouched. This is exactly the case of quantum electrodynamics displaying just three diverging diagrams. This procedure gives observables in very close agreement with experiment as seen e.g. for electron gyromagnetic ratio.
Renormalizability has become an essential criterion for a quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
to be considered as a viable one. All the theories describing fundamental interaction
Fundamental interaction
In particle physics, fundamental interactions are the ways that elementary particles interact with one another...
s, except gravitation
Gravitation
Gravitation, or gravity, is a natural phenomenon by which physical bodies attract with a force proportional to their mass. Gravitation is most familiar as the agent that gives weight to objects with mass and causes them to fall to the ground when dropped...
whose quantum counterpart is presently under very active research, are renormalizable theories.
Nonconvergence of series
An argument by Freeman DysonFreeman Dyson
Freeman John Dyson FRS is a British-born American theoretical physicist and mathematician, famous for his work in quantum field theory, solid-state physics, astronomy and nuclear engineering. Dyson is a member of the Board of Sponsors of the Bulletin of the Atomic Scientists...
shows that the radius of convergence
Radius of convergence
In mathematics, the radius of convergence of a power series is a quantity, either a non-negative real number or ∞, that represents a domain in which the series will converge. Within the radius of convergence, a power series converges absolutely and uniformly on compacta as well...
of the perturbation series in QED is zero. The basic argument goes as follows: if the coupling constant were negative, this would be equivalent to the Coulomb force constant being negative. This would "reverse" the electromagnetic interaction so that like charges would attract and unlike charges would repel. This would render the vacuum unstable against decay into a cluster of electrons on one side of the universe and a cluster of positrons on the other side of the universe. Because the theory is 'sick' for any negative value of the coupling constant, the series do not converge, but are an asymptotic series. This can be taken as a need for a new theory, a problem with perturbation theory
Perturbation theory
Perturbation theory comprises mathematical methods that are used to find an approximate solution to a problem which cannot be solved exactly, by starting from the exact solution of a related problem...
, or ignored by taking a "shut-up-and-calculate" approach.
See also
- Abraham-Lorentz forceAbraham-Lorentz forceIn the physics of electromagnetism, the Abraham–Lorentz force is the recoil force on an accelerating charged particle caused by the particle emitting electromagnetic radiation. It is also called the radiation reaction force....
- Anomalous magnetic moment
- Basics of quantum mechanics
- Bhabha scatteringBhabha scatteringIn quantum electrodynamics, Bhabha scattering is the electron-positron scattering process:There are two leading-order Feynman diagrams contributing to this interaction: an annihilation process and a scattering process. The Bhabha scattering rate is used as a luminosity monitor in electron-positron...
- Cavity quantum electrodynamicsCavity quantum electrodynamicsCavity quantum electrodynamics is the study of the interaction between light confined in a reflective cavity and atoms or other particles, under conditions where the quantum nature of light photons is significant...
- Compton scatteringCompton scatteringIn physics, Compton scattering is a type of scattering that X-rays and gamma rays undergo in matter. The inelastic scattering of photons in matter results in a decrease in energy of an X-ray or gamma ray photon, called the Compton effect...
- Euler-Heisenberg LagrangianEuler-Heisenberg LagrangianIn physics, the Euler-Heisenberg Lagrangian describes the non-linear dynamics of electromagnetic fields in vacuum. It takes into account vacuum polarization to one loop, and it is valid for electromagnetic fields that change slowly compared to the inverse electron mass...
- Feynman path integralsPath integral formulationThe path integral formulation of quantum mechanics is a description of quantum theory which generalizes the action principle of classical mechanics...
- Gauge theoryGauge theoryIn physics, gauge invariance is the property of a field theory in which different configurations of the underlying fundamental but unobservable fields result in identical observable quantities. A theory with such a property is called a gauge theory...
- Gupta-Bleuler formalismGupta-Bleuler formalismIn quantum field theory, the Gupta–Bleuler formalism is a way of quantizing the electromagnetic field. The formulation is due to theoretical physicist Suraj N. Gupta and Konrad Bleuler.Let's start with a single photon first...
- Lamb shift
- Landau poleLandau poleIn physics, the Landau pole is the momentum scale at which the coupling constant of a quantum field theory becomes infinite...
- Moeller scattering
- Photon dynamics in the double-slit experimentPhoton dynamics in the double-slit experimentThe dynamics of photons in the double-slit experiment describes the relationship between classical electromagnetic waves and photons, the quantum counterpart of classical electromagnetic waves, in the context of the double-slit experiment....
- Photon polarizationPhoton polarizationPhoton polarization is the quantum mechanical description of the classical polarized sinusoidal plane electromagnetic wave. Individual photons are completely polarized...
- PositroniumPositroniumPositronium is a system consisting of an electron and its anti-particle, a positron, bound together into an "exotic atom". Being unstable, the two particles annihilate each other to produce two gamma ray photons after an average lifetime of 125 ps or three gamma ray photons after 142 ns in...
- PropagatorPropagatorIn quantum mechanics and quantum field theory, the propagator gives the probability amplitude for a particle to travel from one place to another in a given time, or to travel with a certain energy and momentum. Propagators are used to represent the contribution of virtual particles on the internal...
s
- Quantum chromodynamicsQuantum chromodynamicsIn theoretical physics, quantum chromodynamics is a theory of the strong interaction , a fundamental force describing the interactions of the quarks and gluons making up hadrons . It is the study of the SU Yang–Mills theory of color-charged fermions...
- Quantum field theoryQuantum field theoryQuantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
- Quantum gauge theoryQuantum gauge theoryIn quantum physics, in order to quantize a gauge theory, like for example Yang-Mills theory, Chern-Simons or BF model, one method is to perform a gauge fixing. This is done in the BRST and Batalin-Vilkovisky formulation...
- RenormalizationRenormalizationIn quantum field theory, the statistical mechanics of fields, and the theory of self-similar geometric structures, renormalization is any of a collection of techniques used to treat infinities arising in calculated quantities....
- Scalar electrodynamicsScalar electrodynamicsIn theoretical physics, scalar electrodynamics is a theory of a U gauge field coupled to a charged spin 0 scalar field that takes the place of the Dirac fermions in "ordinary" quantum electrodynamics...
- Schrödinger equationSchrödinger equationThe Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
- Schwinger modelSchwinger modelIn physics, the Schwinger model, named after Julian Schwinger, is the model describing 2D Euclidean quantum electrodynamics with a Dirac fermion. This model exhibits a spontaneous symmetry breaking of the U symmetry due to a chiral condensate due to a pool of instantons. The photon in this model...
- Schwinger-Dyson equationSchwinger-Dyson equationThe Schwinger–Dyson equation , also Dyson-Schwinger equations, named after Julian Schwinger and Freeman Dyson, are general relations between Green functions in quantum field theories...
- Self-energySelf-energyIn theoretical physics and quantum field theory a particle's self-energy \Sigma represents the contribution to the particle's energy, or effective mass, due to interactions between the particle and the system it is part of...
- Standard ModelStandard ModelThe Standard Model of particle physics is a theory concerning the electromagnetic, weak, and strong nuclear interactions, which mediate the dynamics of the known subatomic particles. Developed throughout the mid to late 20th century, the current formulation was finalized in the mid 1970s upon...
- Theoretical and experimental justification for the Schrödinger equationTheoretical and experimental justification for the Schrödinger equationThe theoretical and experimental justification for the Schrödinger equation motivates the discovery of the Schrödinger equation, the equation that describes the dynamics of nonrelativistic particles...
- Vacuum polarizationVacuum polarizationIn quantum field theory, and specifically quantum electrodynamics, vacuum polarization describes a process in which a background electromagnetic field produces virtual electron–positron pairs that change the distribution of charges and currents that generated the original electromagnetic...
- Vertex functionVertex functionIn quantum electrodynamics, the vertex function describes the coupling between a photon and an electron beyond the leading order of perturbation theory...
- Ward–Takahashi identityWard–Takahashi identityIn quantum field theory, a Ward-Takahashi identity is an identity between correlation functions that follows from the global or gauged symmetries of the theory, and which remains valid after renormalization....
- Wheeler-Feynman absorber theory
Books
- Milonni, Peter W., (1994) The quantum vacuum - an introduction to quantum electrodynamics. Academic Press. ISBN 0-12-498080-5