Grashof number
Encyclopedia
The Grashof number 
is a dimensionless number in fluid dynamics
and heat transfer
which approximates the ratio of the buoyancy
to viscous force acting on a fluid. It frequently arises in the study of situations involving natural convection
. It is named after the German engineer Franz Grashof
.
for vertical flat plates
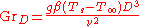for pipes
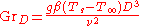for bluff bodies
where the L and D subscripts indicates the length scale basis for the Grashof Number.
The transition to turbulent flow occurs in the range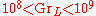
for natural convection from vertical flat plates. At higher Grashof numbers, the boundary layer is turbulent; at lower Grashof numbers, the boundary layer is laminar.
The product of the Grashof number and the Prandtl number gives the Rayleigh number
, a dimensionless number that characterizes convection problems in heat transfer.
There is an analogous form of the Grashof number used in cases of natural convection mass transfer
problems.
where
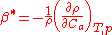
and
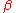as follows:
This partial relation of the volume expansion coefficient,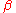
with respect to fluid density, 
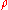and constant pressure can be rewritten as
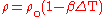
and
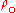- bulk fluid density
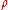- boundary layer density
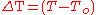- temperature difference between boundary layer and bulk fluid
There are two different ways to find the Grashof Number from this point. One involves the energy equation while the other incorporates the buoyant force due to the difference in density between the boundary layer and bulk fluid.
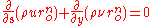
- rotational direction
- tangential velocity
- planar direction
- normal velocity
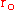- radius
This equation expands to the following with the addition of physical fluid properties:
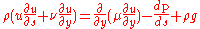
In this equation the superscript n is to differentiate between rotationally symmetric flow from planar flow. The following characteristics of this equation hold true.
- rotationally symmetric flow
- planar, two-dimensional flow
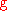- gravitational acceleration
From here we can further simplify the momentum equation by setting the bulk fluid velocity to 0.
This relation shows that the pressure gradient is simply a product of the bulk fluid density and the gravitational acceleration. The next step is to plug in the pressure gradient into the momentum equation.
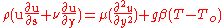
Further simplification of the momentum equation comes by substituting the volume expansion coefficient, density relationship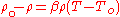
found above into the momentum equation.
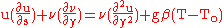
To find the Grashof Number from this point the preceding equation must be non-dimesionalized. This means that every variable in the equation should have no dimension. This is done by dividing each variable by corresponding constant quantities. Lengths are divided by a characteristic length
. Velocities are divided by appropriate reference velocities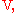 
which considering the Reynolds number gives 
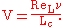Temperatures are divided by the appropriate temperature difference 
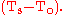These dimensionless parameters look like the following:
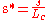
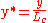
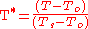
The asteriks represent dimensionless parameter. Combining these dimensionless equations with the momentum equations gives the following simplified equation.
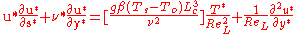
- surface temperature
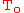- bulk fluid temperature
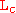- characteristic length
The dimensionless parameter enclosed in the brackets in the preceding equation is known as the Grashof Number
due to the density difference in the boundary layer and the bulk fluid.
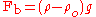
This equation can be manipulated to give,
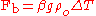
The list of variables that are used in the Buckingham Pi method is listed below, along with their symbols and dimensions.
With reference to the Buckingham Pi Theorem there are 9-5=4 dimensionless groups. Choose L,
k, g and 
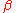as the reference variables. Thus the 
groups are as follows:
,
,
,
.
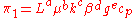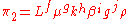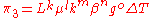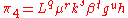Solving these
groups gives:
,
,
,
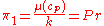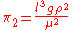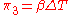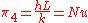
From the two groups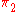
and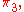 
the product forms the Grashof Number
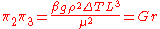
Taking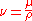
and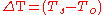 
the preceding equation can be rendered as the same result from deriving the Grashof Number from the energy equation.
In forced convection the Reynolds Number governs the fluid flow. But, in natural convection the Grashof Number is the dimensionless parameter that governs the fluid flow. Using the energy equation and the buoyant force combined with dimensional analysis provides two different ways to derive the Grashof Number.
is a dimensionless number in fluid dynamicsFluid dynamics
In physics, fluid dynamics is a sub-discipline of fluid mechanics that deals with fluid flow—the natural science of fluids in motion. It has several subdisciplines itself, including aerodynamics and hydrodynamics...
and heat transfer
Heat transfer
Heat transfer is a discipline of thermal engineering that concerns the exchange of thermal energy from one physical system to another. Heat transfer is classified into various mechanisms, such as heat conduction, convection, thermal radiation, and phase-change transfer...
which approximates the ratio of the buoyancy
Buoyancy
In physics, buoyancy is a force exerted by a fluid that opposes an object's weight. In a column of fluid, pressure increases with depth as a result of the weight of the overlying fluid. Thus a column of fluid, or an object submerged in the fluid, experiences greater pressure at the bottom of the...
to viscous force acting on a fluid. It frequently arises in the study of situations involving natural convection
Natural convection
Natural convection is a mechanism, or type of heat transport, in which the fluid motion is not generated by any external source but only by density differences in the fluid occurring due to temperature gradients. In natural convection, fluid surrounding a heat source receives heat, becomes less...
. It is named after the German engineer Franz Grashof
Franz Grashof
Franz Grashof was a German engineer. He was a professor of Applied Mechanics at the Technische Hochschule Karlsruhe. He is one of the founding directors of Verein Deutscher Ingenieure in 1855. He developed some early steam-flow formulas but made no significant contribution to free convection.The...
.
for vertical flat plates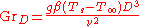 for pipes 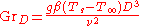for bluff bodieswhere the L and D subscripts indicates the length scale basis for the Grashof Number.
- g = acceleration due to Earth's gravityStandard gravityStandard gravity, or standard acceleration due to free fall, usually denoted by g0 or gn, is the nominal acceleration of an object in a vacuum near the surface of the Earth. It is defined as precisely , or about...
- β = volumetric thermal expansion coefficient (equal to approximately 1/T, for ideal fluids, where T is absolute temperature)
- Ts = surface temperature
- T∞ = bulk temperature
- L = length
- D = diameter
- ν = kinematic viscosity
The transition to turbulent flow occurs in the range
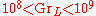for natural convection from vertical flat plates. At higher Grashof numbers, the boundary layer is turbulent; at lower Grashof numbers, the boundary layer is laminar.The product of the Grashof number and the Prandtl number gives the Rayleigh number
Rayleigh number
In fluid mechanics, the Rayleigh number for a fluid is a dimensionless number associated with buoyancy driven flow...
, a dimensionless number that characterizes convection problems in heat transfer.
There is an analogous form of the Grashof number used in cases of natural convection mass transfer
Mass transfer
Mass transfer is the net movement of mass from one location, usually meaning a stream, phase, fraction or component, to another. Mass transfer occurs in many processes, such as absorption, evaporation, adsorption, drying, precipitation, membrane filtration, and distillation. Mass transfer is used...
problems.
where
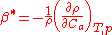
and
- g = acceleration due to Earth's gravityStandard gravityStandard gravity, or standard acceleration due to free fall, usually denoted by g0 or gn, is the nominal acceleration of an object in a vacuum near the surface of the Earth. It is defined as precisely , or about...
- Ca,s = concentration of species a at surface
- Ca,a = concentration of species a in ambient medium
- L = characteristic length
- ν = kinematic viscosity
- ρ = fluidFluidIn physics, a fluid is a substance that continually deforms under an applied shear stress. Fluids are a subset of the phases of matter and include liquids, gases, plasmas and, to some extent, plastic solids....
densityDensityThe mass density or density of a material is defined as its mass per unit volume. The symbol most often used for density is ρ . In some cases , density is also defined as its weight per unit volume; although, this quantity is more properly called specific weight... - Ca = concentration of species a
- T = constant temperature
- p = constant pressure
Derivation of Grashof Number
The first step to deriving the Grashof Number Gr is manipulating the volume expansion coefficient,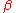 as follows:This partial relation of the volume expansion coefficient,
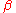with respect to fluid density, 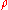and constant pressure can be rewritten as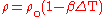and
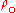- bulk fluid density 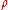- boundary layer density 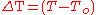- temperature difference between boundary layer and bulk fluidThere are two different ways to find the Grashof Number from this point. One involves the energy equation while the other incorporates the buoyant force due to the difference in density between the boundary layer and bulk fluid.
Energy Equation
This discussion involving the energy equation is with respect to rotationally symmetric flow. This analysis will take into consideration the effect of gravitational acceleration on flow and heat transfer. The mathematical equations to follow apply both to rotational symmetric flow as well as two-dimensional planar flow.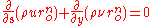 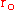- rotational direction - tangential velocity - planar direction - normal velocity - radiusThis equation expands to the following with the addition of physical fluid properties:
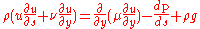
In this equation the superscript n is to differentiate between rotationally symmetric flow from planar flow. The following characteristics of this equation hold true.
- rotationally symmetric flow - planar, two-dimensional flow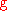 - gravitational accelerationFrom here we can further simplify the momentum equation by setting the bulk fluid velocity to 0.
This relation shows that the pressure gradient is simply a product of the bulk fluid density and the gravitational acceleration. The next step is to plug in the pressure gradient into the momentum equation.
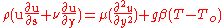
Further simplification of the momentum equation comes by substituting the volume expansion coefficient, density relationship
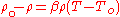found above into the momentum equation.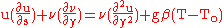To find the Grashof Number from this point the preceding equation must be non-dimesionalized. This means that every variable in the equation should have no dimension. This is done by dividing each variable by corresponding constant quantities. Lengths are divided by a characteristic length
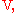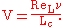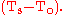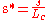
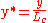
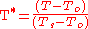
. Velocities are divided by appropriate reference velocities which considering the Reynolds number gives Temperatures are divided by the appropriate temperature difference These dimensionless parameters look like the following: The asteriks represent dimensionless parameter. Combining these dimensionless equations with the momentum equations gives the following simplified equation.
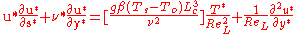
- surface temperature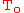 - bulk fluid temperature 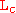- characteristic lengthThe dimensionless parameter enclosed in the brackets in the preceding equation is known as the Grashof Number
Buckingham Pi Theorem
Another form of dimensional analysis that will result in the Grashof Number is known as the Buckingham Pi theorem. This method takes into account the buoyancy force per unit volume, due to the density difference in the boundary layer and the bulk fluid.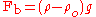This equation can be manipulated to give,
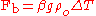
The list of variables that are used in the Buckingham Pi method is listed below, along with their symbols and dimensions.
| Variable | Symbol | Dimensions |
|---|---|---|
| Significant Length |  |
 |
| Fluid Viscosity |  |
 |
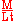| Fluid Heat Capacity |  |
 |
| Fluid Thermal Conductivity |  |
 |
| Volume Expansion Coefficient |  |
 |
| Gravitational Acceleration |  |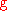
 |
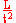| Temperature Difference |  |
 |
| Heat Transfer Coefficient |  |
 |
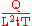With reference to the Buckingham Pi Theorem there are 9-5=4 dimensionless groups. Choose L,
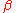k, g and as the reference variables. Thus the groups are as follows: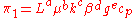,,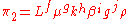,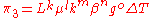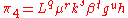.Solving these
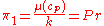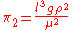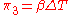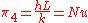
groups gives:,,,From the two groups
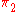and 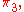the product forms the Grashof Number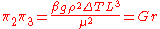Taking
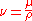and 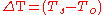the preceding equation can be rendered as the same result from deriving the Grashof Number from the energy equation.In forced convection the Reynolds Number governs the fluid flow. But, in natural convection the Grashof Number is the dimensionless parameter that governs the fluid flow. Using the energy equation and the buoyant force combined with dimensional analysis provides two different ways to derive the Grashof Number.