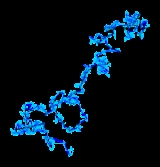
Brownian motion
Encyclopedia

Particle
A particle is, generally, a small localized object to which can be ascribed physical properties. It may also refer to:In chemistry:* Colloidal particle, part of a one-phase system of two or more components where the particles aren't individually visible.In physics:* Subatomic particle, which may be...
.
The mathematical model of Brownian motion has several real-world applications. An often quoted example is stock market
Stock market
A stock market or equity market is a public entity for the trading of company stock and derivatives at an agreed price; these are securities listed on a stock exchange as well as those only traded privately.The size of the world stock market was estimated at about $36.6 trillion...
fluctuations; however, movements in share prices may arise due to unforeseen events which do not repeat themselves.
Brownian motion is among the simplest of the continuous-time stochastic (or probabilistic) processes
Stochastic process
In probability theory, a stochastic process , or sometimes random process, is the counterpart to a deterministic process...
, and it is a limit
Limit (mathematics)
In mathematics, the concept of a "limit" is used to describe the value that a function or sequence "approaches" as the input or index approaches some value. The concept of limit allows mathematicians to define a new point from a Cauchy sequence of previously defined points within a complete metric...
of both simpler and more complicated stochastic processes (see random walk
Random walk
A random walk, sometimes denoted RW, is a mathematical formalisation of a trajectory that consists of taking successive random steps. For example, the path traced by a molecule as it travels in a liquid or a gas, the search path of a foraging animal, the price of a fluctuating stock and the...
and Donsker's theorem
Donsker's theorem
In probability theory, Donsker's theorem, named after M. D. Donsker, identifies a certain stochastic process as a limit of empirical processes. It is sometimes called the functional central limit theorem....
). This universality
Universality (dynamical systems)
In statistical mechanics, universality is the observation that there are properties for a large class of systems that are independent of the dynamical details of the system. Systems display universality in a scaling limit, when a large number of interacting parts come together...
is closely related to the universality of the normal distribution. In both cases, it is often mathematical convenience rather than the accuracy of the models that motivates their use. This is because Brownian motion, whose time derivative is everywhere infinite, is an idealised approximation to actual random physical processes, which always have a finite time scale.
History
The Roman LucretiusLucretius
Titus Lucretius Carus was a Roman poet and philosopher. His only known work is an epic philosophical poem laying out the beliefs of Epicureanism, De rerum natura, translated into English as On the Nature of Things or "On the Nature of the Universe".Virtually no details have come down concerning...
's scientific poem "On the Nature of Things
On the Nature of Things
De rerum natura is a 1st century BC didactic poem by the Roman poet and philosopher Lucretius with the goal of explaining Epicurean philosophy to a Roman audience. The poem, written in some 7,400 dactylic hexameters, is divided into six untitled books, and explores Epicurean physics through richly...
" (c. 60 BC) has a remarkable description of Brownian motion of dust particles. He uses this as a proof of the existence of atoms:
"Observe what happens when sunbeams are admitted into a building and shed light on its shadowy places. You will see a multitude of tiny particles mingling in a multitude of ways... their dancing is an actual indication of underlying movements of matter that are hidden from our sight... It originates with the atoms which move of themselves [i.e., spontaneously]. Then those small compound bodies that are least removed from the impetus of the atoms are set in motion by the impact of their invisible blows and in turn cannon against slightly larger bodies. So the movement mounts up from the atoms and gradually emerges to the level of our senses, so that those bodies are in motion that we see in sunbeams, moved by blows that remain invisible."
Although the mingling motion of dust particles is caused largely by air currents, the glittering, tumbling motion of small dust particles is, indeed, caused chiefly by true Brownian dynamics.
Jan Ingenhousz
Jan Ingenhousz
Jan Ingenhousz or Ingen-Housz FRS was a Dutch physiologist, biologist and chemist. He is best known for showing that light is essential to photosynthesis and thus having discovered photosynthesis. He also discovered that plants, like animals, have cellular respiration...
had described the irregular motion of coal
Coal
Coal is a combustible black or brownish-black sedimentary rock usually occurring in rock strata in layers or veins called coal beds or coal seams. The harder forms, such as anthracite coal, can be regarded as metamorphic rock because of later exposure to elevated temperature and pressure...
dust
Dust
Dust consists of particles in the atmosphere that arise from various sources such as soil dust lifted up by wind , volcanic eruptions, and pollution...
particles on the surface of alcohol
Ethanol
Ethanol, also called ethyl alcohol, pure alcohol, grain alcohol, or drinking alcohol, is a volatile, flammable, colorless liquid. It is a psychoactive drug and one of the oldest recreational drugs. Best known as the type of alcohol found in alcoholic beverages, it is also used in thermometers, as a...
in 1785 - nevertheless the discovery is often credited to the botanist Robert Brown
Robert Brown (botanist)
Robert Brown was a Scottish botanist and palaeobotanist who made important contributions to botany largely through his pioneering use of the microscope...
in 1827. Brown was studying pollen
Pollen
Pollen is a fine to coarse powder containing the microgametophytes of seed plants, which produce the male gametes . Pollen grains have a hard coat that protects the sperm cells during the process of their movement from the stamens to the pistil of flowering plants or from the male cone to the...
grains of the plant Clarkia pulchella
Clarkia pulchella
Clarkia pulchella also known as pinkfairies, ragged robin, and deerhorn clarkia is a species of flowering plant in the Onagraceae family. This wildflower is found in the Pacific Northwest and is the type species of Clarkia...
suspended in water under a microscope when he observed minute particles, ejected by the pollen grains, executing a jittery motion. By repeating the experiment with particles of inorganic matter he was able to rule out that the motion was life-related, although its origin was yet to be explained.
The first person to describe the mathematics behind Brownian motion was Thorvald N. Thiele
Thorvald N. Thiele
Thorvald Nicolai Thiele was a Danish astronomer, actuary and mathematician, most notable for his work in statistics, interpolation and the three-body problem. He was the first to propose a mathematical theory of Brownian motion...
in a paper on the method of least squares
Least squares
The method of least squares is a standard approach to the approximate solution of overdetermined systems, i.e., sets of equations in which there are more equations than unknowns. "Least squares" means that the overall solution minimizes the sum of the squares of the errors made in solving every...
published in 1880. This was followed independently by Louis Bachelier
Louis Bachelier
-External links:** Louis Bachelier webpage at the Université de Franche-Comté, Besançon / France. Text in French.** also from Index Funds Advisors, this discussion of...
in 1900 in his PhD thesis "The theory of speculation", in which he presented a stochastic analysis of the stock and option markets. However, it was Albert Einstein
Albert Einstein
Albert Einstein was a German-born theoretical physicist who developed the theory of general relativity, effecting a revolution in physics. For this achievement, Einstein is often regarded as the father of modern physics and one of the most prolific intellects in human history...
(in one of his 1905 papers) and Marian Smoluchowski
Marian Smoluchowski
Marian Smoluchowski was an ethnic Polish scientist in the Austro-Hungarian Empire. He was a pioneer of statistical physics and an avid mountaineer.-Life:...
(1906) who independently brought the solution of the problem to the attention of physicists, and presented it as a way to indirectly confirm the existence of atoms and molecules.
Einstein's Theory
There are two parts to Einstein's theory: the first part consists in the formulation of a diffusion equation for Brownian particles, in which the diffusion coefficient is related to the mean square displacement of a Brownian particle, while the second part consists in relating the diffusion coefficient to measurable physical quantities. In this way Einstein was able to determine the size of atoms, and how many atoms there are in a mole, or the molecular weight in grams, of a gas. In accordance to Avogadro's lawAvogadro's law
Avogadro's law is a gas law named after Amedeo Avogadro who, in 1811, hypothesized that two given samples of an ideal gas, at the same temperature, pressure and volume, contain the same number of molecules...
this volume is the same for all ideal gases, which is 22,414 cc at standard temperature and pressure. The number of atoms contained in this volume is referred to as Avogadro's number, and the determination of this number is tantamount to the knowledge of the mass of an atom since the latter is obtained by dividing the mass of a mole of the gas by Avogadro's number.
The first part of Einstein's argument was to determine how far a Brownian particle travels in a given time interval. Classical mechanics is unable to determine this distance because of the enormous number of bombardments a Brownian particle will undergo, roughly of the order of
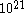 collisions per second. Thus Einstein was led to consider the collective motion of Brownian particles. He showed that if
collisions per second. Thus Einstein was led to consider the collective motion of Brownian particles. He showed that if 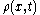 is the density of Brownian particles at point
is the density of Brownian particles at point  at time
at time  , then
, then 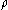 satisfies the diffusion equation:
satisfies the diffusion equation: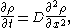
where
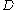 is the mass diffusivity. Assuming that all the particles start from the origin at the initial time
is the mass diffusivity. Assuming that all the particles start from the origin at the initial time 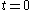 , the diffusion equation has the solution
, the diffusion equation has the solution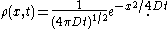
This expression allowed Einstein to calculate the moments directly. The first moment is seen to vanish, meaning that the Brownian particle is equally likely to move to the left as it is to move to the right. The second moment is, however, non-vanishing, being given by
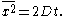
This expresses the mean square displacement in terms of the time elapsed and the diffusivity. From this expression Einstein argued that the displacement of a Brownian particle is not proportional to the elapsed time, but rather to its square root. His argument is based on a conceptual switch from the "ensemble" of Brownian particles to the "single" Brownian particle: we can speak of the relative number of particles at a single instant just as well as of the time it takes a Brownian particle to reach a given point.
The second part of Einstein's theory relates the diffusion constant to physically measurable quantities, such as the mean square displacement of a particle in a given time interval. This result enables the experimental determination of Avogadro's number and therefore the size of molecules. Einstein analyzed a dynamic equilibrium being established between opposing forces. The beauty of his argument is that the final result does not depend upon which forces are involved in setting up the dynamic equilibrium. In his original treatment, Einstein considered an osmotic pressure experiment, but the same conclusion can be reached in other ways. Consider, for instance, particles suspended in a viscous fluid in a gravitational field. Gravity tends to make the particles settle, whereas diffusion acts to homogenize them, driving them into regions of smaller concentration. Under the action of gravity, a particle acquires a downward speed of
 , where
, where 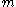 is the mass of the particle,
is the mass of the particle, 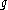 is the acceleration due to gravity, and
is the acceleration due to gravity, and 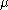 is the particle's mobility
is the particle's mobilityEinstein relation (kinetic theory)
In physics the Einstein relation is a previously unexpected connection revealed independently by Albert Einstein in 1905 and by Marian Smoluchowski in their papers on Brownian motion...
in the fluid. George Stokes had shown that the mobility for a spherical particle with radius
 is
is 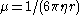 , where
, where 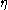 is the dynamic viscosity of the fluid. In a state of dynamic equilibrium, the particles are distributed according to the barometric distribution
is the dynamic viscosity of the fluid. In a state of dynamic equilibrium, the particles are distributed according to the barometric distribution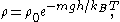
where
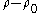 is the difference in density of particles separated by a height difference of
is the difference in density of particles separated by a height difference of 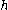 ,
, 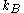 is Boltzmann's constant (namely, the ratio of the universal gas constant,
is Boltzmann's constant (namely, the ratio of the universal gas constant, 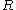 , to Avogadro's number,
, to Avogadro's number, 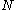 ), and
), and 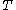 is the absolute temperature. It is Avogadro's number that is to be determined.
is the absolute temperature. It is Avogadro's number that is to be determined.Dynamic equilibrium is established because the more that particles are pulled down by gravity, the greater is the tendency for the particles to migrate to regions of lower concentration. The flux is given by Fick's law,
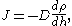
where
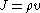 . Introducing the formula for
. Introducing the formula for  , we find that
, we find that
In a state of dynamical equilibrium, this speed must also be equal to
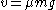 . Notice that both expressions for
. Notice that both expressions for  are proportional to
are proportional to 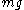 , reflecting how the derivation is independent of the type of forces considered. Equating these two expressions yields a formula for the diffusivity:
, reflecting how the derivation is independent of the type of forces considered. Equating these two expressions yields a formula for the diffusivity:
Here the first equality follows from the first part of Einstein's theory, the third equality follows from the definition of Boltzmann's constant as
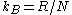 , and the fourth equality follows from Stokes' formula for the mobility. By measuring the mean square displacement over a time interval along with the universal gas constant
, and the fourth equality follows from Stokes' formula for the mobility. By measuring the mean square displacement over a time interval along with the universal gas constant 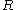 , the temperature
, the temperature  , the viscosity
, the viscosity  , and the particle radius
, and the particle radius  , Avogadro's number
, Avogadro's number 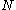 can be determined.
can be determined.The type of dynamical equilibrium proposed by Einstein was not new. It had been pointed out previously by J. J. Thomson
J. J. Thomson
Sir Joseph John "J. J." Thomson, OM, FRS was a British physicist and Nobel laureate. He is credited for the discovery of the electron and of isotopes, and the invention of the mass spectrometer...
in his series of lectures at Yale University in May 1903 that the dynamic equilibrium between the velocity generated by a concentration gradient given by Fick's law and the velocity due to the variation of the partial pressure caused when ions are set in motion "gives us a method of determining Avogadro's Constant which is independent of any hypothesis as to the shape or size of molecules, or of the way in which they act upon each other".
An identical expression to Einstein's formula for the diffusion coefficient was also found by Walther Nernst
Walther Nernst
Walther Hermann Nernst FRS was a German physical chemist and physicist who is known for his theories behind the calculation of chemical affinity as embodied in the third law of thermodynamics, for which he won the 1920 Nobel Prize in chemistry...
in 1888 in which he expressed the diffusion coefficient as the ratio of the osmotic pressure to the ratio of the frictional force and the velocity to which it gives rise. The former was equated to the law of van 't Hoff while the latter was given by Stokes's law. He writes
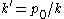 for the diffusion coefficient
for the diffusion coefficient 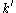 , where
, where  is the osmotic pressure and
is the osmotic pressure and 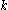 is the ratio of the frictional force to the molecular viscosity which he assumes is given by Stokes's formula for the viscosity. Introducing the ideal gas law per unit volume for the osmotic pressure, the formula becomes identical to that of Einstein's. The use of Stokes's law in Nernst's case, as well as in Einstein and Smoluchowski, is not strictly applicable since it does not apply to the case where the radius of the sphere is small in comparison with the mean free path.
is the ratio of the frictional force to the molecular viscosity which he assumes is given by Stokes's formula for the viscosity. Introducing the ideal gas law per unit volume for the osmotic pressure, the formula becomes identical to that of Einstein's. The use of Stokes's law in Nernst's case, as well as in Einstein and Smoluchowski, is not strictly applicable since it does not apply to the case where the radius of the sphere is small in comparison with the mean free path.At first the predictions of Einstein's formula were seemingly refuted by a series of experiments by Svedberg in 1906 and 1907, which gave displacements of the particles as 4 to 6 times the predicted value, and by Henri in 1908 who found displacements 3 times greater than Einstein's formula predicted. But Einstein's predictions were finally confirmed in a series of experiments carried out by Chaudesaigues in 1908 and Perrin in 1909. The confirmation of Einstein's theory constituted empirical progress for the kinetic theory of heat. In essence, Einstein showed that the motion can be predicted directly from the kinetic model of thermal equilibrium. The importance of the theory lay in the fact that it confirmed the kinetic theory's account of the second law of thermodynamics
Thermodynamics
Thermodynamics is a physical science that studies the effects on material bodies, and on radiation in regions of space, of transfer of heat and of work done on or by the bodies or radiation...
as being an essentially statistical law.
Intuitive metaphor
Consider a large balloon of 100 metres in diameter. Imagine this large balloon in a football stadium. The balloon is so large that it lies on top of many members of the crowd. Because they are excited, these fans hit the balloon at different times and in different directions with the motions being completely random. In the end, the balloon is pushed in random directions, so it should not move on average. Consider now the force exerted at a certain time. We might have 20 supporters pushing right, and 21 other supporters pushing left, where each supporter is exerting equivalent amounts of force. In this case, the forces exerted towards the left and the right are imbalanced in favor of the left; the balloon will move slightly to the left. This type of imbalance exists at all times, and it causes random motion of the balloon. If we look at this situation from far above, so that we cannot see the supporters, we see the large balloon as a small object animated by erratic movement.| Brownian motion model of the trajectory of a particle of dye in water. |
Consider the particles emitted by Brown's pollen grain moving randomly in water: we know that a water molecule is about 0.1 by 0.2 nm in size, whereas the particles which Brown observed were of the order of a few micrometre
Micrometre
A micrometer , is by definition 1×10-6 of a meter .In plain English, it means one-millionth of a meter . Its unit symbol in the International System of Units is μm...
s in size (these are not to be confused with the actual pollen particle which is about 100 micrometres). So a particle from the pollen may be likened to the balloon, and the water molecules to the fans, except that in this case the balloon is surrounded by fans. The Brownian motion of a particle in a liquid is thus due to the instantaneous imbalance in the combined forces exerted by collisions of the particle with the much smaller liquid molecules (which are in random thermal
Temperature
Temperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot...
motion) surrounding it.
An animation of the Brownian motion concept is available as a Java applet
Java applet
A Java applet is an applet delivered to users in the form of Java bytecode. Java applets can run in a Web browser using a Java Virtual Machine , or in Sun's AppletViewer, a stand-alone tool for testing applets...
.
Smoluchowski model
SmoluchowskiMarian Smoluchowski
Marian Smoluchowski was an ethnic Polish scientist in the Austro-Hungarian Empire. He was a pioneer of statistical physics and an avid mountaineer.-Life:...
's theory of Brownian motion starts from the same premise as that of Einstein and derives the same probability distribution
 for the displacement of a Brownian particle along the
for the displacement of a Brownian particle along the  in time
in time  . He therefore gets the same expression for the mean square displacement:
. He therefore gets the same expression for the mean square displacement: 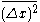 . However, when he relates it to a particle of mass
. However, when he relates it to a particle of mass  moving at a velocity
moving at a velocity  which is the result of a frictional force governed by Stokes's law, he finds
which is the result of a frictional force governed by Stokes's law, he finds
where
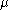 is the viscosity coefficient, and
is the viscosity coefficient, and  is the radius of the particle. Associating the kinetic energy
is the radius of the particle. Associating the kinetic energy  with the thermal energy
with the thermal energy 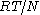 , the expression for the mean square displacement is 64/27 times that found by Einstein. The fraction 27/64 was commented on by Arnold Sommerfeld in his necrology on Smoluckowski: "The numerical coefficient of Einstein, which differs from Smoluchowski by 27/64 can only be put in doubt."
, the expression for the mean square displacement is 64/27 times that found by Einstein. The fraction 27/64 was commented on by Arnold Sommerfeld in his necrology on Smoluckowski: "The numerical coefficient of Einstein, which differs from Smoluchowski by 27/64 can only be put in doubt."Smoluchowski attempts to answer the question of why a Brownian particle should be displaced by bombardments of smaller particles when the probabilities for striking it in the forward and rear directions are equal. In order to do so, he uses, unknowingly, the ballot theorem, first proved by W.A. Whitworth in 1887. The ballot theorem states that if a candidate A scores
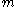 votes and candidate B scores
votes and candidate B scores  that the probability throughout the counting that A will have more votes than B is
that the probability throughout the counting that A will have more votes than B is  or
or  , no matter how large the total number of votes
, no matter how large the total number of votes  may be. In other words, if one candidate has an edge on the other candidate he will tend to keep that edge even though there is nothing favoring either candidate on a ballot extraction.
may be. In other words, if one candidate has an edge on the other candidate he will tend to keep that edge even though there is nothing favoring either candidate on a ballot extraction.If the probability of
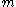 gains and
gains and  losses follows a binomial distribution,
losses follows a binomial distribution,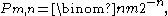
with equal a priori probabilities of
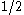 , the mean total gain is
, the mean total gain is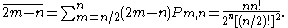
If
 is large enough so that Stirling's approximation can be used in the form
is large enough so that Stirling's approximation can be used in the form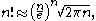
then the expected total gain will be
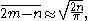
showing that it increases as the square root of the total population.
Suppose that a Brownian particle of mass
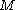 is surrounded by lighter particles of mass
is surrounded by lighter particles of mass 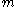 which are traveling at a speed
which are traveling at a speed  . Then, reasons Smoluchowski, in any collision between a surrounding and Brownian particles, the velocity transmitted to the latter will be
. Then, reasons Smoluchowski, in any collision between a surrounding and Brownian particles, the velocity transmitted to the latter will be  . This ratio is of the order of
. This ratio is of the order of  cm/sec. But we also have to take into consideration that in a gas there will be more than
cm/sec. But we also have to take into consideration that in a gas there will be more than 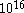 collisions in a second, and even greater in a liquid where we expect that there will be
collisions in a second, and even greater in a liquid where we expect that there will be  collision in one second. Some of these collisions will tend to accelerate the Brownian particle; others will tend to decelerate it. If there is a mean excess of one kind of collision or the other to be of the order of
collision in one second. Some of these collisions will tend to accelerate the Brownian particle; others will tend to decelerate it. If there is a mean excess of one kind of collision or the other to be of the order of 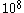 to
to 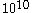 collisions in one second, then velocity of the Brownian particle may be anywhere between 10 to a 1000 cm/sec. Thus, even though there are equal probabilities for forward and backward collisions there will be a net tendency to keep the Brownian particle in motion, just as the ballot theorem predicts.
collisions in one second, then velocity of the Brownian particle may be anywhere between 10 to a 1000 cm/sec. Thus, even though there are equal probabilities for forward and backward collisions there will be a net tendency to keep the Brownian particle in motion, just as the ballot theorem predicts.These orders of magnitude are not exact because they don't take into consideration the velocity of the Brownian particle,
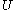 , which depends on the collisions that tend to accelerate and decelerate it. The larger
, which depends on the collisions that tend to accelerate and decelerate it. The larger 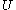 is, the greater will be the collisions that will retard it so that the velocity of a Brownian particle can never increase without limit. Could a such a process occur, it would be tantamount to a perpetual motion of the second type. And since equipartition of energy applies, the kinetic energy of the Brownian particle,
is, the greater will be the collisions that will retard it so that the velocity of a Brownian particle can never increase without limit. Could a such a process occur, it would be tantamount to a perpetual motion of the second type. And since equipartition of energy applies, the kinetic energy of the Brownian particle, 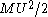 , will be equal, on the average, to the kinetic energy of the surrounding fluid particle,
, will be equal, on the average, to the kinetic energy of the surrounding fluid particle, 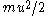 .
.In 1906 Smoluchowski published a one-dimensional model to describe a particle undergoing Brownian motion. The model assumes collisions with M m where M is the test particle's mass and m the mass of one of the individual particles composing the fluid. It is assumed that the particle collisions are confined to one dimension and that it is equally probable for the test particle to be hit from the left as from the right. It is also assumed that every collision always imparts the same magnitude of
 . If
. If 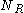 is the number of collisions from the right and
is the number of collisions from the right and 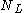 the number of collisions from the left then after N collisions the particle's velocity will have changed by
the number of collisions from the left then after N collisions the particle's velocity will have changed by 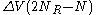 . The multiplicity
. The multiplicityMultiplicity (mathematics)
In mathematics, the multiplicity of a member of a multiset is the number of times it appears in the multiset. For example, the number of times a given polynomial equation has a root at a given point....
is then simply given by:
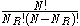
and the total number of possible states is given by
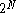 . Therefore the probability of the particle being hit from the right
. Therefore the probability of the particle being hit from the right 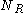 times is:
times is: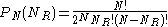
As a result of its simplicity, Smoluchowski's 1D model can only qualitatively describe Brownian motion. For a realistic particle undergoing Brownian motion in a fluid many of the assumptions cannot be made. For example, the assumption that on average there occurs an equal number of collisions from the right as from the left falls apart once the particle is in motion. Also, there would be a distribution of different possible
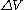 s instead of always just one in a realistic situation.
s instead of always just one in a realistic situation.Modeling using differential equations
The equations governing Brownian motion relate slightly differently to each of the two definitions of Brownian motion given at the start of this article.Mathematics
In mathematicsMathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Brownian motion is described by the Wiener process; a continuous-time stochastic process
Stochastic process
In probability theory, a stochastic process , or sometimes random process, is the counterpart to a deterministic process...
named in honor of Norbert Wiener
Norbert Wiener
Norbert Wiener was an American mathematician.A famous child prodigy, Wiener later became an early researcher in stochastic and noise processes, contributing work relevant to electronic engineering, electronic communication, and control systems.Wiener is regarded as the originator of cybernetics, a...
. It is one of the best known Lévy process
Lévy process
In probability theory, a Lévy process, named after the French mathematician Paul Lévy, is any continuous-time stochastic process that starts at 0, admits càdlàg modification and has "stationary independent increments" — this phrase will be explained below...
es (càdlàg
Càdlàg
In mathematics, a càdlàg , RCLL , or corlol function is a function defined on the real numbers that is everywhere right-continuous and has left limits everywhere...
stochastic processes with stationary
Stationary process
In the mathematical sciences, a stationary process is a stochastic process whose joint probability distribution does not change when shifted in time or space...
independent
Statistical independence
In probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...
increments) and occurs frequently in pure and applied mathematics, economics
Economy
An economy consists of the economic system of a country or other area; the labor, capital and land resources; and the manufacturing, trade, distribution, and consumption of goods and services of that area...
and physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
.
The Wiener process
 is characterised by three facts:
is characterised by three facts:
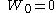
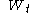 is almost surelyAlmost surelyIn probability theory, one says that an event happens almost surely if it happens with probability one. The concept is analogous to the concept of "almost everywhere" in measure theory...
is almost surelyAlmost surelyIn probability theory, one says that an event happens almost surely if it happens with probability one. The concept is analogous to the concept of "almost everywhere" in measure theory...
continuous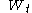 has independent increments with distribution
has independent increments with distribution 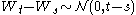 (for
(for 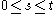 ).
).
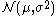 denotes the normal distribution with expected value
denotes the normal distribution with expected valueExpected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
μ and variance
Variance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
σ2. The condition that it has independent increments means that if
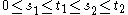 then
then 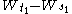 and
and 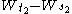 are independent random variables.
are independent random variables.An alternative characterisation of the Wiener process is the so-called Lévy characterisation that says that the Wiener process is an almost surely continuous martingale
Martingale (probability theory)
In probability theory, a martingale is a model of a fair game where no knowledge of past events can help to predict future winnings. In particular, a martingale is a sequence of random variables for which, at a particular time in the realized sequence, the expectation of the next value in the...
with
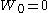 and quadratic variation
and quadratic variationQuadratic variation
In mathematics, quadratic variation is used in the analysis of stochastic processes such as Brownian motion and martingales. Quadratic variation is just one kind of variation of a process.- Definition :...
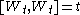 .
.A third characterisation is that the Wiener process has a spectral representation as a sine series whose coefficients are independent
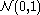 random variables. This representation can be obtained using the Karhunen–Loève theorem.
random variables. This representation can be obtained using the Karhunen–Loève theorem.The Wiener process can be constructed as the scaling limit
Scaling limit
In physics or mathematics, the scaling limit is a term applied to the behaviour of a lattice model in the limit of the lattice spacing going to zero. A lattice model which approximates a continuum quantum field theory in the limit as the lattice spacing goes to zero corresponds to finding a second...
of a random walk
Random walk
A random walk, sometimes denoted RW, is a mathematical formalisation of a trajectory that consists of taking successive random steps. For example, the path traced by a molecule as it travels in a liquid or a gas, the search path of a foraging animal, the price of a fluctuating stock and the...
, or other discrete-time stochastic processes with stationary independent increments. This is known as Donsker's theorem
Donsker's theorem
In probability theory, Donsker's theorem, named after M. D. Donsker, identifies a certain stochastic process as a limit of empirical processes. It is sometimes called the functional central limit theorem....
. Like the random walk, the Wiener process is recurrent in one or two dimensions (meaning that it returns almost surely to any fixed neighborhood of the origin infinitely often) whereas it is not recurrent in dimensions three and higher. Unlike the random walk, it is scale invariant
Scale invariance
In physics and mathematics, scale invariance is a feature of objects or laws that do not change if scales of length, energy, or other variables, are multiplied by a common factor...
.
The time evolution of the position of the Brownian particle itself can be described approximately by a Langevin equation
Langevin equation
In statistical physics, a Langevin equation is a stochastic differential equation describing the time evolution of a subset of the degrees of freedom. These degrees of freedom typically are collective variables changing only slowly in comparison to the other variables of the system...
, an equation which involves a random force field representing the effect of the thermal fluctuations
Thermal fluctuations
In statistical mechanics, thermal fluctuations are random deviations of a system from its equilibrium. All thermal fluctuations become larger and more frequent as the temperature increases, and likewise they disappear altogether as temperature approaches absolute zero.Thermal fluctuations are a...
of the solvent on the Brownian particle. On long timescales, the mathematical Brownian motion is well described by a Langevin equation. On small timescales, inertia
Inertia
Inertia is the resistance of any physical object to a change in its state of motion or rest, or the tendency of an object to resist any change in its motion. It is proportional to an object's mass. The principle of inertia is one of the fundamental principles of classical physics which are used to...
l effects are prevalent in the Langevin equation. However the mathematical Brownian motion is exempt of such inertial effects. Note that inertial effects have to be considered in the Langevin equation, otherwise the equation becomes singular. so that simply removing the inertia
Inertia
Inertia is the resistance of any physical object to a change in its state of motion or rest, or the tendency of an object to resist any change in its motion. It is proportional to an object's mass. The principle of inertia is one of the fundamental principles of classical physics which are used to...
term from this equation would not yield an exact description, but rather a singular behavior in which the particle doesn't move at all.
Physics
The diffusion equation yields an approximation of the time evolution of the probability density functionProbability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
associated to the position of the particle going under a Brownian movement under the physical definition. The approximation is valid on short
Langevin equation
In statistical physics, a Langevin equation is a stochastic differential equation describing the time evolution of a subset of the degrees of freedom. These degrees of freedom typically are collective variables changing only slowly in comparison to the other variables of the system...
timescales.
The time evolution of the position of the Brownian particle itself is best described using Langevin equation
Langevin equation
In statistical physics, a Langevin equation is a stochastic differential equation describing the time evolution of a subset of the degrees of freedom. These degrees of freedom typically are collective variables changing only slowly in comparison to the other variables of the system...
, an equation which involves a random force field representing the effect of the thermal fluctuations
Thermal fluctuations
In statistical mechanics, thermal fluctuations are random deviations of a system from its equilibrium. All thermal fluctuations become larger and more frequent as the temperature increases, and likewise they disappear altogether as temperature approaches absolute zero.Thermal fluctuations are a...
of the solvent on the particle.
The displacement of a particle undergoing Brownian motion is obtained by solving the diffusion equation under appropriate boundary conditions and finding the rms
Root mean square
In mathematics, the root mean square , also known as the quadratic mean, is a statistical measure of the magnitude of a varying quantity. It is especially useful when variates are positive and negative, e.g., sinusoids...
of the solution. This shows that the displacement varies as the square root of the time (not linearly), which explains why previous experimental results concerning the velocity of Brownian particles gave nonsensical results. A linear time dependence was incorrectly assumed.
At very short time scales, however, the motion of a particle is dominated by its inertia and its displacement will be linearly dependent on time: Δx = vΔt. So the instantaneous velocity of the Brownian motion can be measured as v = Δx/Δt, when Δt << τ, where τ is the momentum relaxation time. In 2010, the instantaneous velocity of a Brownian particle (a glass microsphere trapped in air with an optical tweezer) was measured successfully. The velocity data verified the Maxwell-Boltzmann velocity distribution, and the equipartition theorem for a Brownian particle.
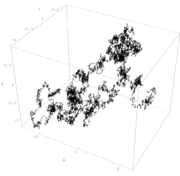
The Brownian motion can be modeled by a random walk. Random walks in porous media or fractals are anomalous.
In the general case, Brownian motion is a non-Markov random process
Markov process
In probability theory and statistics, a Markov process, named after the Russian mathematician Andrey Markov, is a time-varying random phenomenon for which a specific property holds...
and described by stochastic integral equations
Stochastic calculus
Stochastic calculus is a branch of mathematics that operates on stochastic processes. It allows a consistent theory of integration to be defined for integrals of stochastic processes with respect to stochastic processes...
.
Lévy characterisation
The French mathematicianMathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
Paul Lévy
Paul Pierre Lévy
Paul Pierre Lévy was a Jewish French mathematician who was active especially in probability theory, introducing martingales and Lévy flights...
proved the following theorem, which gives a necessary and sufficient condition for a continuous Rn-valued stochastic process X to actually be n-dimensional Brownian motion. Hence, Lévy's condition can actually be used as an alternative definition of Brownian motion.
Let X = (X1, ..., Xn) be a continuous stochastic process on a probability space
Probability space
In probability theory, a probability space or a probability triple is a mathematical construct that models a real-world process consisting of states that occur randomly. A probability space is constructed with a specific kind of situation or experiment in mind...
(Ω, Σ, P) taking values in Rn. Then the following are equivalent:
- X is a Brownian motion with respect to P, i.e., the law of X with respect to P is the same as the law of an n-dimensional Brownian motion, i.e., the push-forward measure X∗(P) is classical Wiener measure on C0([0, +∞); Rn).
- both
- X is a martingaleMartingale (probability theory)In probability theory, a martingale is a model of a fair game where no knowledge of past events can help to predict future winnings. In particular, a martingale is a sequence of random variables for which, at a particular time in the realized sequence, the expectation of the next value in the...
with respect to P (and its own natural filtrationNatural filtrationIn the theory of stochastic processes in mathematics and statistics, the natural filtration associated to a stochastic process is a filtration associated to the process which records its "past behaviour" at each time...
); and - for all 1 ≤ i, j ≤ n, Xi(t)Xj(t) −δijt is a martingale with respect to P (and its own natural filtrationNatural filtrationIn the theory of stochastic processes in mathematics and statistics, the natural filtration associated to a stochastic process is a filtration associated to the process which records its "past behaviour" at each time...
), where δij denotes the Kronecker delta.
- X is a martingale
Riemannian manifold

Infinitesimal generator (stochastic processes)
In mathematics — specifically, in stochastic analysis — the infinitesimal generator of a stochastic process is a partial differential operator that encodes a great deal of information about the process...
(and hence characteristic operator) of a Brownian motion on Rn is easily calculated to be ½Δ, where Δ denotes the Laplace operator
Laplace operator
In mathematics the Laplace operator or Laplacian is a differential operator given by the divergence of the gradient of a function on Euclidean space. It is usually denoted by the symbols ∇·∇, ∇2 or Δ...
. This observation is useful in defining Brownian motion on an m-dimensional Riemannian manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
(M, g): a Brownian motion on M is defined to be a diffusion on M whose characteristic operator
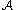 in local coordinates xi, 1 ≤ i ≤ m, is given by ½ΔLB, where ΔLB is the Laplace–Beltrami operator given in local coordinates by
in local coordinates xi, 1 ≤ i ≤ m, is given by ½ΔLB, where ΔLB is the Laplace–Beltrami operator given in local coordinates by
where [gij] = [gij]−1 in the sense of the inverse of a square matrix.
Gravitational motion
In stellar dynamicsStellar dynamics
Stellar dynamics is the branch of astrophysics which describes in a statistical way the collective motions of stars subject to their mutual gravity. The long range of gravity and the slow "relaxation" of stellar systems prevent the use of the methods of statistical physics...
, a massive body (star, black hole
Black hole
A black hole is a region of spacetime from which nothing, not even light, can escape. The theory of general relativity predicts that a sufficiently compact mass will deform spacetime to form a black hole. Around a black hole there is a mathematically defined surface called an event horizon that...
, etc.) can experience Brownian motion as it responds to gravitational forces from surrounding stars. The rms velocity
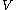 of the massive object, of mass
of the massive object, of mass 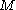 , is related to the rms velocity
, is related to the rms velocity 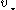 of the background stars by
of the background stars by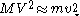
where
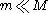 is the mass of the background stars. The gravitational force from the massive object causes nearby stars to move faster than they otherwise would, increasing both
is the mass of the background stars. The gravitational force from the massive object causes nearby stars to move faster than they otherwise would, increasing both 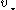 and
and 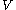 . The Brownian velocity of Sgr A*, the supermassive black hole
. The Brownian velocity of Sgr A*, the supermassive black holeSupermassive black hole
A supermassive black hole is the largest type of black hole in a galaxy, in the order of hundreds of thousands to billions of solar masses. Most, and possibly all galaxies, including the Milky Way, are believed to contain supermassive black holes at their centers.Supermassive black holes have...
at the center of the Milky Way galaxy, is predicted from this formula to be less than 1 km s−1.
Narrow escape
The Narrow escape problemNarrow escape problem
The narrow escape problem is a ubiquitous problem in biology, biophysics and cellular biology.The formulation is the following: a Brownian particle is confined to a bounded domain by a reflecting boundary, except for a small window through which it can escape. The narrow escape problem is that...
is an ubiquitous problem in biology, biophysics and cellular biology which has the following formulation: a Brownian particle
Brownian motion
Brownian motion or pedesis is the presumably random drifting of particles suspended in a fluid or the mathematical model used to describe such random movements, which is often called a particle theory.The mathematical model of Brownian motion has several real-world applications...
(ion
Ion
An ion is an atom or molecule in which the total number of electrons is not equal to the total number of protons, giving it a net positive or negative electrical charge. The name was given by physicist Michael Faraday for the substances that allow a current to pass between electrodes in a...
, molecule
Molecule
A molecule is an electrically neutral group of at least two atoms held together by covalent chemical bonds. Molecules are distinguished from ions by their electrical charge...
, or protein
Protein
Proteins are biochemical compounds consisting of one or more polypeptides typically folded into a globular or fibrous form, facilitating a biological function. A polypeptide is a single linear polymer chain of amino acids bonded together by peptide bonds between the carboxyl and amino groups of...
) is confined to a bounded domain (a compartment or a cell) by a reflecting boundary, except for a small window through which it can escape. The narrow escape problem is that of calculating the mean escape time. This time diverges as the window shrinks, thus rendering the calculation a singular perturbation
Singular perturbation
In mathematics, more precisely in perturbation theory, a singular perturbation problem is a problem containing a small parameter that cannot be approximated by setting the parameter value to zero...
problem.
Popular culture
Science fiction author Douglas AdamsDouglas Adams
Douglas Noel Adams was an English writer and dramatist. He is best known as the author of The Hitchhiker's Guide to the Galaxy, which started life in 1978 as a BBC radio comedy before developing into a "trilogy" of five books that sold over 15 million copies in his lifetime, a television...
included Brownian motion in his description of a Finite Improbability Generator in his work The Hitchhiker's Guide to the Galaxy
The Hitchhiker's Guide to the Galaxy
The Hitchhiker's Guide to the Galaxy is a science fiction comedy series created by Douglas Adams. Originally a radio comedy broadcast on BBC Radio 4 in 1978, it was later adapted to other formats, and over several years it gradually became an international multi-media phenomenon...
. Said generator required a source of truly random motion and this was provided by an atomic vector plotter suspended in "a fresh cup of really hot tea".
See also
- Brownian bridgeBrownian bridgeA Brownian bridge is a continuous-time stochastic process B whose probability distribution is the conditional probability distribution of a Wiener process W given the condition that B = B = 0.The expected value of the bridge is zero, with variance t, implying that the most...
: a Brownian motion that is required to "bridge" specified values at specified times - Brownian covariance
- Brownian dynamics
- Brownian motorBrownian motorBrownian motors are nano-scale or molecular devices by which thermally activated processes are controlled and used to generate directed motion in space and to do mechanical or electrical work...
- Brownian ratchetBrownian ratchetIn the philosophy of thermal and statistical physics, the Brownian ratchet, or Feynman-Smoluchowski ratchet is a thought experiment about an apparent perpetual motion machine first analysed in 1912 by Polish physicist Marian Smoluchowski and popularised by American Nobel laureate physicist Richard...
- Brownian surfaceBrownian surfaceA Brownian surface is a fractal surface generated via a fractal elevation function.For instance, in the three-dimensional case, where two variables X and Y are given as coordinates, the elevation function between any two points and can be set to have a mean or expected value that increases as the...
- Brownian treeBrownian treeA Brownian tree, whose name is derived from Robert Brown via Brownian motion, is a form of computer art that was briefly popular in the 1990s, when home computers started to have sufficient power to simulate Brownian motion...
- Rotational Brownian motionRotational Brownian motionRotational Brownian motion is the random change in the orientation of a polar molecule due to collisions with other molecules. It is an important element of theories of dielectric materials....
- Complex systemComplex systemA complex system is a system composed of interconnected parts that as a whole exhibit one or more properties not obvious from the properties of the individual parts....
- Diffusion equation
- Geometric Brownian motionGeometric Brownian motionA geometric Brownian motion is a continuous-time stochastic process in which the logarithm of the randomly varying quantity follows a Brownian motion, also called a Wiener process...
- Itō diffusionIto diffusionIn mathematics — specifically, in stochastic analysis — an Itō diffusion is a solution to a specific type of stochastic differential equation. That equation is similar to the Langevin equation, used in Physics to describe the brownian motion of a particle subjected to a potential in a...
: a generalisation of Brownian motion - Langevin equationLangevin equationIn statistical physics, a Langevin equation is a stochastic differential equation describing the time evolution of a subset of the degrees of freedom. These degrees of freedom typically are collective variables changing only slowly in comparison to the other variables of the system...
- Lévy arcsine lawLévy arcsine lawIn probability theory, the Lévy arcsine law, found by , states that the probability distribution of the proportion of the time that a Wiener process is positive is a random variable whose probability distribution is the arcsine distribution...
- Local time (mathematics)Local time (mathematics)In the mathematical theory of stochastic processes, local time is a stochastic process associated with diffusion processes such as Brownian motion, that characterizes the amount of time a particle has spent at a given level...
- Mark G. RaizenMark G. RaizenMark George Raizen is a physicist who conducts experiments on quantum optics and atom optics.-Birth and Education:Raizen was born in New York City where generations of his family resided since the 1840s. While he comes from a long line of medical doctors, dating back to the Civil War, Raizen's life...
- OsmosisOsmosisOsmosis is the movement of solvent molecules through a selectively permeable membrane into a region of higher solute concentration, aiming to equalize the solute concentrations on the two sides...
- Random walkRandom walkA random walk, sometimes denoted RW, is a mathematical formalisation of a trajectory that consists of taking successive random steps. For example, the path traced by a molecule as it travels in a liquid or a gas, the search path of a foraging animal, the price of a fluctuating stock and the...
- Red noise, also known as brown noise (Martin GardnerMartin GardnerMartin Gardner was an American mathematics and science writer specializing in recreational mathematics, but with interests encompassing micromagic, stage magic, literature , philosophy, scientific skepticism, and religion...
proposed this name for sound generated with random intervals. It is a pun on Brownian motion and white noiseWhite noiseWhite noise is a random signal with a flat power spectral density. In other words, the signal contains equal power within a fixed bandwidth at any center frequency...
.) - Schramm–Loewner evolution
- Surface diffusionSurface diffusionSurface diffusion is a general process involving the motion of adatoms, molecules, and atomic clusters at solid material surfaces. The process can generally be thought of in terms of particles jumping between adjacent adsorption sites on a surface, as in figure 1...
: a type of constrained Brownian motion. - Tyndall effectTyndall effectThe Tyndall effect, also known as Tyndall scattering, is light scattering by particles in a colloid or particles in a fine suspension. It is named after the 19th century physicist John Tyndall. It is similar to Rayleigh scattering, in that the intensity of the scattered light depends on the fourth...
: physical chemistry phenomenon where particles are involved; used to differentiate between the different types of mixtures. - UltramicroscopeUltramicroscopeAn ultramicroscope is a system of illumination for viewing tiny particles. When the diameter of a particle is below or near the wavelength of light , the particle cannot be seen in a light microscope with the usual method of illumination. The ultramicroscope system is based on light scattering, not...
- Single particle trackingSingle particle trackingSingle particle tracking is the observation of the motion of individual particles within a medium. The coordinates over a series of time steps is referred to as a trajectory. The trajectory can be analyzed to identify modes of motion or heterogeneities in the motion such as obstacles or regions...
- Nanoparticle Tracking AnalysisNanoparticle tracking analysisNanoparticle Tracking Analysis is a method for visualizing and analyzing particles in liquids that relates the rate of Brownian motion to particle size. The rate of movement is related only to the viscosity and temperature of the liquid, it is not influenced by particle density or refractive index...
- Marangoni effectMarangoni effectThe Marangoni effect is the mass transfer along an interface between two fluids due to surface tension gradient...
- Narrow escape problemNarrow escape problemThe narrow escape problem is a ubiquitous problem in biology, biophysics and cellular biology.The formulation is the following: a Brownian particle is confined to a bounded domain by a reflecting boundary, except for a small window through which it can escape. The narrow escape problem is that...
Further reading
- Brown, Robert, "A brief account of microscopical observations made in the months of June, July and August, 1827, on the particles contained in the pollen of plants; and on the general existence of active molecules in organic and inorganic bodies." Phil. Mag. 4, 161–173, 1828. (PDF version of original paper including a subsequent defense by Brown of his original observations, Additional remarks on active molecules.)
- Clark, P. (1976) 'Atomism versus thermodynamics' in Method and appraisal in the physical sciences, Colin Howson (Ed), Cambridge University Press 1976
- Einstein, A. "Investigations on the Theory of Brownian Movement". New York: Dover, 1956. ISBN 0-486-60304-0 http://lorentz.phl.jhu.edu/AnnusMirabilis/AeReserveArticles/eins_brownian.pdf
- Henri, V(1908) 'Etudes cinematographique du mouvement brownien' Comptes Rendus 146 pp 1024–6
- LucretiusLucretiusTitus Lucretius Carus was a Roman poet and philosopher. His only known work is an epic philosophical poem laying out the beliefs of Epicureanism, De rerum natura, translated into English as On the Nature of Things or "On the Nature of the Universe".Virtually no details have come down concerning...
, 'On The Nature of Things.', translated by William Ellery Leonard. (on-line version, from Project GutenbergProject GutenbergProject Gutenberg is a volunteer effort to digitize and archive cultural works, to "encourage the creation and distribution of eBooks". Founded in 1971 by Michael S. Hart, it is the oldest digital library. Most of the items in its collection are the full texts of public domain books...
. see the heading 'Atomic Motions'; this translation differs slightly from the one quoted). - Pearle, P., Collett, B., Bart, K., Bilderback, D., Newman, D., and Samuels, S. (2010) What Brown saw and you can too. Am. J. Phys. 78: 1278-1289.
- Nelson, Edward, Dynamical Theories of Brownian Motion (1967) (PDF version of this out-of-print book, from the author's webpage.)
- J. PerrinJean Baptiste PerrinJean Baptiste Perrin was a French physicist and Nobel laureate.-Early years:Born in Lille, France, Perrin attended the École Normale Supérieure, the elite grande école in Paris. He became an assistant at the school during the period of 1894-97 when he began the study of cathode rays and X-rays...
, "Mouvement brownien et réalité moléculaire". Ann. Chim. Phys.Annales de chimie et de physiqueAnnales de chimie et de physique is a scientific journal that was founded in Paris, France, in 1789 under the title Annales de chimie. One of the early editors was the French chemist Antoine Lavoisier. In 1815, it became the Annales de chimie et de physique, and was published under that name for...
8ième série 18, 5–114 (1909). See also Perrin's book "Les Atomes" (1914). - Ruben D. Cohen (1986) "Self Similarity in Brownian Motion and Other Ergodic Phenomena", Journal of Chemical Education 63, pp. 933–934 http://rdcohen.50megs.com/BrownianMotion.pdf
- Svedberg, T. Studien zur Lehre von den kolloiden Losungen 1907
- Theile, T. N. Danish version: "Om Anvendelse af mindste Kvadraters Methode i nogle Tilfælde, hvor en Komplikation af visse Slags uensartede tilfældige Fejlkilder giver Fejlene en ‘systematisk’ Karakter". French version: "Sur la compensation de quelques erreurs quasi-systématiques par la méthodes de moindre carrés" published simultaneously in Vidensk. Selsk. Skr. 5. Rk., naturvid. og mat. Afd., 12:381–408, 1880.
External links
- Brownian motion java simulation
- Article for the school-going child
- Einstein on Brownian Motion
- Brownian Motion, "Diverse and Undulating"
- Short Movie on Brownian Motion
- Discusses history, botany and physics of Brown's original observations, with videos
- "Einstein's prediction finally witnessed one century later" : a test to observe the velocity of Brownian motion

