
Iterated function system
Encyclopedia
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, iterated function systems or IFSs are a method of constructing fractal
Fractal
A fractal has been defined as "a rough or fragmented geometric shape that can be split into parts, each of which is a reduced-size copy of the whole," a property called self-similarity...
s; the resulting constructions are always self-similar.
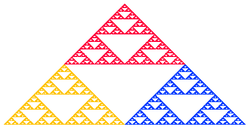
IFS fractals, as they are normally called, can be of any number of dimensions, but are commonly computed and drawn in 2D. The fractal is made up of the union of several copies of itself, each copy being transformed by a function (hence "function system"). The canonical example is the Sierpinski gasket also called the Sierpinski triangle. The functions are normally contractive
Contraction mapping
In mathematics, a contraction mapping, or contraction, on a metric space is a function f from M to itself, with the property that there is some nonnegative real number k...
which means they bring points closer together and make shapes smaller. Hence the shape of an IFS fractal is made up of several possibly-overlapping smaller copies of itself, each of which is also made up of copies of itself, ad infinitum
Ad infinitum
Ad infinitum is a Latin phrase meaning "to infinity."In context, it usually means "continue forever, without limit" and thus can be used to describe a non-terminating process, a non-terminating repeating process, or a set of instructions to be repeated "forever," among other uses...
. This is the source of its self-similar fractal nature.
Definition
Formally, an iterated function system is a finite set of contraction mappingContraction mapping
In mathematics, a contraction mapping, or contraction, on a metric space is a function f from M to itself, with the property that there is some nonnegative real number k...
s on a complete metric space. Symbolically,

is an iterated function system if each
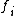 is a contraction on the complete metric space
is a contraction on the complete metric space 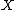 .
.Properties
Hutchinson (1981) showed that, for the metric space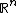 , such a system of functions has a unique compact
, such a system of functions has a unique compactCompact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
(closed and bounded) fixed set S. One way of constructing a fixed set is to start with an initial point or set S0 and iterate the actions of the fi, taking Sn+1 to be the union of the image of Sn under the fi ; then taking S to be the closure
Closure (topology)
In mathematics, the closure of a subset S in a topological space consists of all points in S plus the limit points of S. Intuitively, these are all the points that are "near" S. A point which is in the closure of S is a point of closure of S...
of the union of the Sn. Symbolically, the unique fixed (nonempty compact) set
 has the property
has the property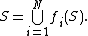
The set S is thus the fixed set of the Hutchinson operator
Hutchinson operator
In mathematics, in the study of fractals, a Hutchinson operator is a collection of functions on an underlying space E...

The existence and uniqueness of S is a consequence of the contraction mapping principle as is the fact that
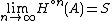
for any nonempty compact set
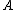 in
in 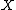 . Random elements of S may be obtained by the "chaos game" below.
. Random elements of S may be obtained by the "chaos game" below.The collection of functions
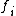 generates
generatesGenerating set
In mathematics, the expressions generator, generate, generated by and generating set can have several closely related technical meanings:...
a monoid
Monoid
In abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
under composition
Function composition
In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
. If there are only two such functions, the monoid can be visualized as a binary tree
Binary tree
In computer science, a binary tree is a tree data structure in which each node has at most two child nodes, usually distinguished as "left" and "right". Nodes with children are parent nodes, and child nodes may contain references to their parents. Outside the tree, there is often a reference to...
, where, at each node of the tree, one may compose with the one or the other function (i.e. take the left or the right branch). In general, if there are k functions, then one may visualize the monoid as a full k-ary tree
K-ary tree
In graph theory, a k-ary tree is a rooted tree in which each node has no more than k children. It is also sometimes known as a k-way tree, an N-ary tree, or an M-ary tree.A binary tree is the special case where k=2....
, also known as a Cayley tree.
Constructions

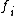 is required to be a linear
is required to be a linearLinear transformation
In mathematics, a linear map, linear mapping, linear transformation, or linear operator is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0...
,
or more generally an affine transformation
Affine transformation
In geometry, an affine transformation or affine map or an affinity is a transformation which preserves straight lines. It is the most general class of transformations with this property...
and hence represented by a matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
. However, IFSs may also be built from non-linear functions, including projective transformations and Möbius transformations. The Fractal flame
Fractal flame
Fractal flames are a member of the iterated function system class of fractals created by Scott Draves in 1992. Draves' open-source code was later ported into Adobe After Effects graphics software and translated into the Apophysis fractal flame editor....
is an example of an IFS with nonlinear functions.
The most common algorithm to compute IFS fractals is called the chaos game
Chaos game
In mathematics, the term chaos game, as coined by Michael Barnsley, originally referred to a method of creating a fractal, using a polygon and an initial point selected at random inside it...
. It consists of picking a random point in the plane, then iteratively applying one of the functions chosen at random from the function system and drawing the point. An alternative algorithm is to generate each possible sequence of functions up to a given maximum length, and then to plot the results of applying each of these sequences of functions to an initial point or shape.
Each of these algorithms provides a global construction which generates points distributed across the whole fractal. If a small area of the fractal is being drawn, many of these points will fall outside of the screen boundaries. This makes zooming into an IFS construction normally impractical.
Although the theory of IFS requires each function to be contractive, in practice software that implements IFS only require that the whole system be contractive on average.
Examples
The diagram shows the construction on an IFS from two affine functions. The functions are represented by their effect on the bi-unit square (the function transforms the outlined square into the shaded square). The combination of the two functions forms the Hutchinson operatorHutchinson operator
In mathematics, in the study of fractals, a Hutchinson operator is a collection of functions on an underlying space E...
. Three iterations of the operator are shown, and then the final image is of the fixed point, the final fractal.
Early examples of fractals which may be generated by an IFS include the Cantor set
Cantor set
In mathematics, the Cantor set is a set of points lying on a single line segment that has a number of remarkable and deep properties. It was discovered in 1875 by Henry John Stephen Smith and introduced by German mathematician Georg Cantor in 1883....
, first described in 1884; and de Rham curve
De Rham curve
In mathematics, a de Rham curve is a certain type of fractal curve named in honor of Georges de Rham.The Cantor function, Césaro curve, Minkowski's question mark function, the Lévy C curve, the blancmange curve and the Koch curve are all special cases of the general de Rham...
s, a type of self-similar curve described by Georges de Rham
Georges de Rham
Georges de Rham was a Swiss mathematician, known for his contributions to differential topology.He studied at the University of Lausanne and then in Paris for a doctorate, becoming a lecturer in Lausanne in 1931; where he held positions until retirement in 1971; he held positions in Geneva in...
in 1957.

History
IFS were conceived in their present form by John E. Hutchinson in 1981 and popularized by Michael BarnsleyMichael Barnsley
Michael Fielding Barnsley is a British mathematician, researcher and an entrepreneur who has worked on fractal compression; he holds several patents on the technology. He received his Ph.D in Theoretical Chemistry from University of Wisconsin–Madison in 1972...
's book Fractals Everywhere.
--Michael Barnsley et al.
See also
.jpg)
- L-systemL-systemAn L-system or Lindenmayer system is a parallel rewriting system, namely a variant of a formal grammar, most famously used to model the growth processes of plant development, but also able to model the morphology of a variety of organisms...
- Fractal compressionFractal compressionFractal compression is a lossy compression method for digital images, based on fractals. The method is best suited for textures and natural images, relying on the fact that parts of an image often resemble other parts of the same image...
- Fractal flameFractal flameFractal flames are a member of the iterated function system class of fractals created by Scott Draves in 1992. Draves' open-source code was later ported into Adobe After Effects graphics software and translated into the Apophysis fractal flame editor....
- Complex base systemsComplex base systemsIn arithmetic, a complex base system is a positional numeral system whose radix is an imaginary or complex number In arithmetic, a complex base system is a positional numeral system whose radix is an imaginary (proposed by Donald Knuth in 1955) or complex number In arithmetic, a complex base...
External links
- A definition of IFS and a Java illustration with several built-in examples at cut-the-knotCut-the-knotCut-the-knot is a free, advertisement-funded educational website maintained by Alexander Bogomolny and devoted to popular exposition of many topics in mathematics. The site has won more than 20 awards from scientific and educational publications, including a Scientific American Web Award in 2003,...

