
Self-similarity
Encyclopedia
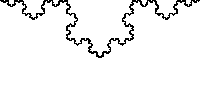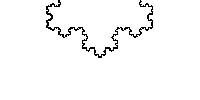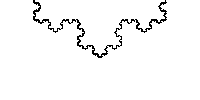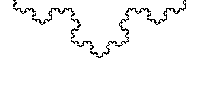
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a self-similar object is exactly or approximately similar
Similarity (geometry)
Two geometrical objects are called similar if they both have the same shape. More precisely, either one is congruent to the result of a uniform scaling of the other...
to a part of itself (i.e. the whole has the same shape as one or more of the parts). Many objects in the real world, such as coastlines, are statistically self-similar: parts of them show the same statistical properties at many scales. Self-similarity is a typical property of fractal
Fractal
A fractal has been defined as "a rough or fragmented geometric shape that can be split into parts, each of which is a reduced-size copy of the whole," a property called self-similarity...
s.
Scale invariance
Scale invariance
In physics and mathematics, scale invariance is a feature of objects or laws that do not change if scales of length, energy, or other variables, are multiplied by a common factor...
is an exact form of self-similarity where at any magnification there is a smaller piece of the object that is similar
Similarity (geometry)
Two geometrical objects are called similar if they both have the same shape. More precisely, either one is congruent to the result of a uniform scaling of the other...
to the whole. For instance, a side of the Koch snowflake
Koch snowflake
The Koch snowflake is a mathematical curve and one of the earliest fractal curves to have been described...
is both symmetrical and scale-invariant; it can be continually magnified 3x without changing shape.
Definition
A compactCompact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
X is self-similar if there exists a finite set S indexing a set of non-surjective homeomorphism
Homeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
s
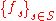 for which
for which
If
 , we call X self-similar if it is the only non-empty subset
, we call X self-similar if it is the only non-empty subsetSubset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of Y such that the equation above holds for
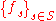 . We call
. We call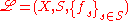
a self-similar structure. The homeomorphisms may be iterated
Iterated function
In mathematics, an iterated function is a function which is composed with itself, possibly ad infinitum, in a process called iteration. In this process, starting from some initial value, the result of applying a given function is fed again in the function as input, and this process is repeated...
, resulting in an iterated function system
Iterated function system
In mathematics, iterated function systems or IFSs are a method of constructing fractals; the resulting constructions are always self-similar....
. The composition of functions creates the algebraic structure of a monoid
Monoid
In abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
. When the set S has only two elements, the monoid is known as the dyadic monoid. The dyadic monoid can be visualized as an infinite binary tree
Binary tree
In computer science, a binary tree is a tree data structure in which each node has at most two child nodes, usually distinguished as "left" and "right". Nodes with children are parent nodes, and child nodes may contain references to their parents. Outside the tree, there is often a reference to...
; more generally, if the set S has p elements, then the monoid may be represented as a p-adic
P-adic number
In mathematics, and chiefly number theory, the p-adic number system for any prime number p extends the ordinary arithmetic of the rational numbers in a way different from the extension of the rational number system to the real and complex number systems...
tree.
The automorphism
Automorphism
In mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism...
s of the dyadic monoid is the modular group
Modular group
In mathematics, the modular group Γ is a fundamental object of study in number theory, geometry, algebra, and many other areas of advanced mathematics...
; the automorphisms can be pictured as hyperbolic rotations of the binary tree.
Examples

Mandelbrot set
The Mandelbrot set is a particular mathematical set of points, whose boundary generates a distinctive and easily recognisable two-dimensional fractal shape...
is also self-similar around Misiurewicz point
Misiurewicz point
A Misiurewicz point is a parameter in the Mandelbrot set for which the critical point is strictly preperiodic . By analogy, the term Misiurewicz point is also used for parameters in a Multibrot set where the unique critical point is strictly preperiodic...
s.
Self-similarity has important consequences for the design of computer networks, as typical network traffic has self-similar properties. For example, in teletraffic engineering
Teletraffic engineering
Telecommunications traffic engineering, teletraffic engineering, or traffic engineering is the application of traffic engineering theory to telecommunications...
, packet switched data traffic patterns seem to be statistically self-similar. This property means that simple models using a Poisson distribution
Poisson distribution
In probability theory and statistics, the Poisson distribution is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time and/or space if these events occur with a known average rate and independently of the time since...
are inaccurate, and networks designed without taking self-similarity into account are likely to function in unexpected ways.
Similarly, stock market
Stock market
A stock market or equity market is a public entity for the trading of company stock and derivatives at an agreed price; these are securities listed on a stock exchange as well as those only traded privately.The size of the world stock market was estimated at about $36.6 trillion...
movements are described as displaying self-affinity
Self-affinity
In mathematics, self-affinity refers to a fractal whose pieces are scaled by different amounts in the x- and y-directions. We refer to these as being the 2-dimensional axes, like that of a grid. This means that in order to appreciate the self similarity of these fractal objects, they have to be...
, i.e. they appear self-similar when transformed via an appropriate affine transformation
Affine transformation
In geometry, an affine transformation or affine map or an affinity is a transformation which preserves straight lines. It is the most general class of transformations with this property...
for the level of detail being shown.
Self-similarity can be found in nature, as well. At right is a mathematically-generated, perfectly self-similar image of a fern, which bears a marked resemblance to natural ferns. Other plants, such as Romanesco broccoli
Romanesco broccoli
Romanesco broccoli, or Roman cauliflower, is an edible flower of the species Brassica oleracea, and a variant form of cauliflower.-History:Romanesco broccoli was first documented in Italy in the sixteenth century...
, exhibit strong self-similarity.
In music, a Shepard tone
Shepard tone
A Shepard tone, named after Roger Shepard, is a sound consisting of a superposition of sine waves separated by octaves. When played with the base pitch of the tone moving upward or downward, it is referred to as the Shepard scale. This creates the auditory illusion of a tone that continually...
is self-similar in the frequency or wavelength domains.
See also
- Droste effectDroste effectThe Droste effect is a specific kind of recursive picture, one that in heraldry is termed mise en abyme. An image exhibiting the Droste effect depicts a smaller version of itself in a place where a similar picture would realistically be expected to appear. This smaller version then depicts an even...
- RecursionRecursionRecursion is the process of repeating items in a self-similar way. For instance, when the surfaces of two mirrors are exactly parallel with each other the nested images that occur are a form of infinite recursion. The term has a variety of meanings specific to a variety of disciplines ranging from...
- Self-referenceSelf-referenceSelf-reference occurs in natural or formal languages when a sentence or formula refers to itself. The reference may be expressed either directly—through some intermediate sentence or formula—or by means of some encoding...
- Zipf's law
- Self-dissimilaritySelf-dissimilaritySelf-dissimilarity is a measure of complexity defined in a series of papers by David Wolpert and William G. Macready....
External links
- "Copperplate Chevrons" — a self-similar fractal zoom movie
- "Self-Similarity" — New articles about the Self-Similarity. Waltz Algorithm

