Parameter space
Encyclopedia
In science
, a parameter space is the set of values of parameter
s encountered in a particular mathematical model
. Often the parameters are input
s of a function
, in which case the technical term for the parameter space is domain of a function.
Parameter spaces are particularly useful for describing families of probability distribution
s that depend on parameters. More generally in science, the term parameter space is used to describe experimental variables. For example, the concept has been used in the science of soccer in the article "Parameter space for successful soccer kicks." In the study, "Success rates are determined through the use of four-dimensional parameter space volumes."
In the context of statistics
, parameter spaces form the background for parameter estimation.
As Ross (1990) describes in his book:
The idea of intentionally truncating the parameter space has also been advanced elsewhere.
where i2 = −1.
The famous Mandelbrot set
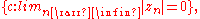
where z0 = 0, and for n > 0,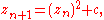
is a subset
of this parameter space. The function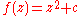
is a complex quadratic polynomial
.
the parameters are amplitude
A > 0, angular frequency
ω > 0, and phase
φ ∈ S1. Thus the parameter space is
from the confines of three-dimensional space
. For instance, the parameter space of spheres in three dimensions, has four dimensions -- three for the sphere center and another for the radius. According to Dirk Struik, it was the book Neue Geometrie des Raumes (1849) by Julius Plücker
that showed
The requirement for higher dimensions is illustrated by Plücker's line geometry. Struik writes
Science
Science is a systematic enterprise that builds and organizes knowledge in the form of testable explanations and predictions about the universe...
, a parameter space is the set of values of parameter
Parameter
Parameter from Ancient Greek παρά also “para” meaning “beside, subsidiary” and μέτρον also “metron” meaning “measure”, can be interpreted in mathematics, logic, linguistics, environmental science and other disciplines....
s encountered in a particular mathematical model
Mathematical model
A mathematical model is a description of a system using mathematical concepts and language. The process of developing a mathematical model is termed mathematical modeling. Mathematical models are used not only in the natural sciences and engineering disciplines A mathematical model is a...
. Often the parameters are input
Input
Input is the term denoting either an entrance or changes which are inserted into a system and which activate/modify a process. It is an abstract concept, used in the modeling, system design and system exploitation...
s of a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
, in which case the technical term for the parameter space is domain of a function.
Parameter spaces are particularly useful for describing families of probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
s that depend on parameters. More generally in science, the term parameter space is used to describe experimental variables. For example, the concept has been used in the science of soccer in the article "Parameter space for successful soccer kicks." In the study, "Success rates are determined through the use of four-dimensional parameter space volumes."
In the context of statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, parameter spaces form the background for parameter estimation.
As Ross (1990) describes in his book:
- Parameter space is a subset of p-dimensional space consisting of the set of values of Θ which are allowable in a particular model. The values may sometimes be constrainted, say to the positive quadrant or the unit square, or in case of symmetry, to the triangular region where, say
The idea of intentionally truncating the parameter space has also been advanced elsewhere.
Examples
- In complex dynamicsComplex dynamicsComplex dynamics is the study of dynamical systems defined by iteration of functions on complex number spaces. Complex analytic dynamics is the study of the dynamics of specifically analytic functions.-Techniques:*General** Montel's theorem...
the parameter space is the complex planeComplex planeIn mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
- C = { z = x + y i : x, y ∈ R }
where i2 = −1.
The famous Mandelbrot set
Mandelbrot set
The Mandelbrot set is a particular mathematical set of points, whose boundary generates a distinctive and easily recognisable two-dimensional fractal shape...
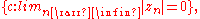
where z0 = 0, and for n > 0,
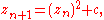is a subsetSubset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of this parameter space. The function
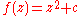is a complex quadratic polynomialComplex quadratic polynomial
A complex quadratic polynomial is a quadratic polynomial whose coefficients are complex numbers.-Forms:When the quadratic polynomial has only one variable , one can distinguish its 4 main forms:...
.
- In a sine waveSine waveThe sine wave or sinusoid is a mathematical function that describes a smooth repetitive oscillation. It occurs often in pure mathematics, as well as physics, signal processing, electrical engineering and many other fields...
model
the parameters are amplitude
Amplitude
Amplitude is the magnitude of change in the oscillating variable with each oscillation within an oscillating system. For example, sound waves in air are oscillations in atmospheric pressure and their amplitudes are proportional to the change in pressure during one oscillation...
A > 0, angular frequency
Angular frequency
In physics, angular frequency ω is a scalar measure of rotation rate. Angular frequency is the magnitude of the vector quantity angular velocity...
ω > 0, and phase
Phase (waves)
Phase in waves is the fraction of a wave cycle which has elapsed relative to an arbitrary point.-Formula:The phase of an oscillation or wave refers to a sinusoidal function such as the following:...
φ ∈ S1. Thus the parameter space is
History
Parameter space contributed to the liberation of geometryGeometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
from the confines of three-dimensional space
Three-dimensional space
Three-dimensional space is a geometric 3-parameters model of the physical universe in which we live. These three dimensions are commonly called length, width, and depth , although any three directions can be chosen, provided that they do not lie in the same plane.In physics and mathematics, a...
. For instance, the parameter space of spheres in three dimensions, has four dimensions -- three for the sphere center and another for the radius. According to Dirk Struik, it was the book Neue Geometrie des Raumes (1849) by Julius Plücker
Julius Plücker
Julius Plücker was a German mathematician and physicist. He made fundamental contributions to the field of analytical geometry and was a pioneer in the investigations of cathode rays that led eventually to the discovery of the electron. He also vastly extended the study of Lamé curves.- Early...
that showed
- ...geometry need not solely be based on points as basic elements. Lines, planes, circles, spheres can all be used as the elements (Raumelemente) on which a geometry can be based. This fertile conception threw new light on both synthetic and algebraic geometry and created new forms of duality. The number of dimensions of a particular form of geometry could now be any positive number, depending on the number of parameters necessary to define the "element".
The requirement for higher dimensions is illustrated by Plücker's line geometry. Struik writes
- [Plücker's] geometry of lines in three-space could be considered as a four-dimensional geometry, or, as KleinFelix KleinChristian Felix Klein was a German mathematician, known for his work in group theory, function theory, non-Euclidean geometry, and on the connections between geometry and group theory...
has stressed, as the geometry of a four-dimensional quadricQuadricIn mathematics, a quadric, or quadric surface, is any D-dimensional hypersurface in -dimensional space defined as the locus of zeros of a quadratic polynomial...
in a five-dimensional space.